Vectors and Matrices Assignment

Vectors and Matrices

TABLE OF CONTENT
TASK 1............................................................................................................................................1
1.1 Probabilities of familiar events .............................................................................................1
1.2 Relative frequencies as probability measure ........................................................................4
1.3 Combined probabilities .........................................................................................................6
1. 4 Binomial, Poisson and Gaussian distribution ......................................................................7
1.5 Simple problem solutions using nCr, nPr and n! ..................................................................9
TASK 2............................................................................................................................................9
2.1 Estimates of modalism, skew and standard deviation ..........................................................9
...................................................................................................................................................10
2.2 Confidence intervals and standard error..............................................................................11
2.3 Implications of central limit theorem (CLT).......................................................................12
2.4 Probability of statistics and interpretations of the results ...................................................12

TASK 1
1.1 Probabilities of familiar events
Mutually exclusive:
These are defined as the events which cannot occur simultaneously. For instance the
event A is defined as occurrence of head and event B is known as occurrence of tail while
tossing a coin. When event A occurs then, it is not possible that event B will occur. Such types of
events in which A∩B = 0 then A and B are called mutually exclusive events.
Conditional probability:
The probability of an event A is called conditional probability when the occurrence of a
depends upon the knowledge of other event B which has already occurred. The conditional
probability of A is represented by P (A, B) and is given by:
P (A|B) = P (A and B) / P (A)
Dependent and independent:
The two events are known as dependent events when the outcomes of first event affect
the occurrence or probability of other event. For example if two events A and B are dependent
then their probability can be derived by using formula of conditional probability.
Similarly, the events whose occurrence does not depend upon the occurrence of another
event are known as independent events. When two events A and B are independent then they
satisfy the following relation:
P (A and B) = P (A). P (B)
1.
Two fair spinners with faces numbered 1-4
Probability of spinner indicating sum of 5 = ?
Solution
Possible outcomes of both the spinners= (1, 1) (1, 2) (1, 3) (1, 4)
(2, 1) (2, 2) (2, 3) (2, 4)
(3, 1) (3, 2) (3, 3) (3, 4)
(4, 1) (4, 2) (4, 3) (4, 4)
Total number of outcomes = 16
Favourable number of outcomes with sum equals to 5 and number 3 on at least one spinner = 2
1

[(3, 2) (2, 3)]
Required probability = 2/16 = 1/8
2.)
P(C) = 0.2
P (D) = 0.6
P (C| D) = 0.3
Solution
From the formula of conditional probability we have:
P (C| D) = P (C ∩ D) / P(C)
On putting values from above we get:
P (C ∩ D) = 0.3 * 0.2 = 0.06
P (D| C) = P (C ∩ D) / P(D) = 0.06 / 0.6 = 0.1
P (C U D) = P (C) + P (D) - P (C ∩ D)
P (C U D) = 0.2 + 0.6 – 0.06 = 0.74
Now using the formula: P (C' ∩ D') = 1 - P (C U D)
P (C' ∩ D') = 1 – 0.74 = 0.26
Using the formula: P (C' ∩ D) = P (D) - (C ∩ D)
= 0.6 – 0.06 = 0.54
P (D| C) = 0.1
P (C' ∩ D') = 0.26
P (C' ∩ D) = 0.54
3.)
Total number of cards = 52
Probability of card to be an ace, given that it is diamond = ?
Solution
Let A be the event that card is an ace and B is that event that card is diamond
Required probability = P (A|B)
2

P (B) = 13/52 = 0.25
P (A and B) = p (A ∩ B) = 1/52 = 0.019
P (A|B) = p (A ∩ B) / P (B) = 0.076
Calculate probabilities
1.)
A and B are mutually exclusive events.
P (A) = 0.2
P (B) = 0.4
Solution
a.) P (A U B)
For the mutually exclusive events: P (A U B) = P (A) + P (B)
P (A U B) = 0.2 +0.4 = 0.6
b.) P (A ∩ B')
P (A ∩ B') = P (A) - (A ∩ B)
For mutually exclusive events (A ∩ B)= 0 so
P (A ∩ B') = P (A) – 0 = 0.2
c.) P (A' ∩ B')
P (A' ∩ B') = 1 - P (A U B) = 1 – 0.6 = 0.4
2.)
A and B are independent events
P (A) = ¼ = 0.25
P (B) = 1/5 = 0.2
Solution
a.) P (A ∩ B)
For independent events P (A ∩ B) = P (A). P (B)
P (A ∩ B)= 0.25 * 0.2 = 0.05
b.) P (A ∩ B')
P (A ∩ B') = P (A) - P (A ∩ B) = 0.25 – 0.05 = 0.2
3

P (A ∩ B') = 0.2
c.) P (A' ∩ B')
P (A U B) = P (A) + P (B) - P (A ∩ B)
= 0.25 + 0.2 – 0.05 = 0.4
P (A' ∩ B') = 1 - P (A U B) = 1- 0.4
P (A' ∩ B') = 0.6
3.)
Number of red beads = 3
Number of blue beads = 5
Total beads in bag = 8
Solution
a.) Probability that both beads are blue
Required probability = (5/8) * (5/8) = 25/64 = 0.39
P (Both beads are blue) = 0.39
b.) Probability that second bead is blue
Required probability = P (both are blue) + P (First is red and second is blue)
= 0.39 + [(3/8) * (5/8)] = 0.62
P (second bead is blue) = 0.62
1.2 Relative frequencies as probability measure
No. of meals a day Frequency
1 6
2 23
3 56
4 14
a.) Relative frequency of choosing a person eating 3 meals a day
4

Solution:
Frequency of people having 3 meals per day = 56
Relative frequency = 56/100 = 0.56
b.)
Total number of participants = 75
Relative frequency (f) = favourable number of outcomes (p) / Total outcomes (t)
f = p/t
From the above we have f = 0.56 = Relative frequency of people having 3 meals in a day
t = 75
p = f*t
p = 75*0.56 = 42
Out of 75, around 42 people are expected to have 3 meals
2.)
The result of 20 throws of biased dice:
3 4 2 3 1 5 6 2 4 3
4 3 1 1 6 2 5 6 5 3
Solution
a.) Relative frequency of each score
Score Frequency Relative frequency
1 3 3/20= 0.15
2 3 3/20= 0.15
3 5 5/20= 0.25
4 3 3/20= 0.15
5 3 3/20= 0.15
5

6 3 3/20= 0.15
b.)
Number of throws = 60
Relative frequency of getting a score of 3 = 0.25 (From the above table)
Expected number of times when score 3 can occur = 60 * 0.25 = 15
c.)
Probability of getting 3 when a fair dice is thrown = 1/6
Expected number of times 3 can be scored when dice is thrown 60 times = (1/6) * 60 = 10
Thus, it can be concluded that for the same number of trials fair dice is expected to give 3 only
10 times while the unfair dice is expected to give same score 15 times.
1.3 Combined probabilities
1.)
Spinner has Red = 3
Blue = 2
Green = 2
Total = 7
Solution
a.)
P (Red and blue) = (3/7) * (2/7)
P (Red and blue) = 0.12
b.)
P (at least 1 blue)= (2/7) * (1/7)
P (at least 1 blue)= 0.04
2.)
Total number of marbles = 12
6

Red = 2 Blue = 4 Green = 6
Solution
a.) P (same colour twice) = P (Both red) + P (Both blue) +P (Both green)
P (Both red) = (2/12) * (2/12) = 0.02
P (Both blue)= (4/12) * (4/12) = 0.11
P (Both green)= (6/12) * (6/12) = 0.25
P (same colour twice) = 0.02 + 0.11 +0.25 = 0.38
b.) P (Not blue) = Probability of getting red or green in both iterations
P of getting red = 2/12
P of getting green = 6/12
P of not getting blue in the first iteration = (2/12) + (6/12) = 0.66
P of not getting blue in the second iteration = (2/12) + (6/12) = 0.66
Total probability of not getting blue = P (Not blue) = 0.66 * 0.66 = 0.43
1. 4 Binomial, Poisson and Gaussian distribution
1.)
Total customers = 10
Let A be the event that customer will ask for water with meal and x is number of customers
P (A) = 3/5 = 0.6
Solution
a.)
Probability that exactly 6 customers demand water with meal = P (x = 6)
Using the formula of binomial distribution we have:
P (x) = nCr * (p^x) * (q^(n-x)) where q = 1-p
x = 6 p = 0.6 q= 0.4 n = 10
P (x=6) = 10C6 * (0.6^6) * (0.4^4)
= 210* 0.046 * 0.025 = 0.24
Required P (x=6) = 0.24
b.)
7

P ( x<9) = ?
P (x<9) = 1- [P (x = 10) + P (x = 9)]
P (x = 10) = 10C10 * (0.6^10) * (1) = 0.006
P (x = 9) = 10C9 * (0.6^9) * (0.4^1) = 0.04
P (x<9) = 1 – [0.006 + 0.04]
P (x<9) = 0.954
2.)
Let x be the number of sales made and n is the number of calls
p = 0.15 q = 0.85
a.)
Using binomial distribution
P (x=0, n=10) = 10C0 * (0.15)^0 * (0.85)^10 = 0.196
P (no sales made in 10 calls) = 0.196
b.) P (x>3, n= 20)
P (x>3) = 1 – p (x<3)
P (x<3) = p (x =0) + p (x =1) + p (x =2)
= [20C0 * (0.15)^0 * (0.85)^20] + [20C1 * (0.15)^1 * (0.85)^19] + [20C2 * (0.15)^2 *
(0.85)^18]
P (x<3) = 0.64
P (x>3) = 1 – 0.64 = 0.35
P (more than 3 sales made in 20 calls) = 0.35
3.)
Let x is the number of patients arriving at hospital in 90 minute period.
The rate of arrival of patients in 90 min = (6/60) * 90 = 9
a.) P (x = 7)
P (x=7) ={ [ (9)^7 ] * e^(-9) } / 7!
P (x=7) = 0.11
8

b.)
P (x >= 10) = 1 – P (x<= 9)
P (x<= 9) = 0.58
P (x >= 10) = 1 – 0.58 = 0.42
4.)
Let x denotes the number of power cuts
The rate of power cuts = 3 per year
n = 3
a.)
P (x= 7) = { [ (3)^7 ] * e^(-3) } / 7!
P (x= 7) = 0.0216
b.)
P (x>= 4) = 1 - P (x<= 3)
P (x<= 3) = 0.64
P (x>= 4) = 1 – 0.64
P (x>= 4) = 0.35
1.5 Simple problem solutions using nCr, nPr and n!
1.)
10! = 10*9*8*7*6*5*4*3*2*1 = 3628800
10! = 3628800
2.)
Permutation for n = 5 and r = 3
Permutation = n! / (n-r)! = 5! / (5-3)! = 60
3.)
Combination for n = 5 and r = 3
Combination = n! /[ r! *(n-r)!] = 5! /[ 3! *(5-3)!] = 10
9

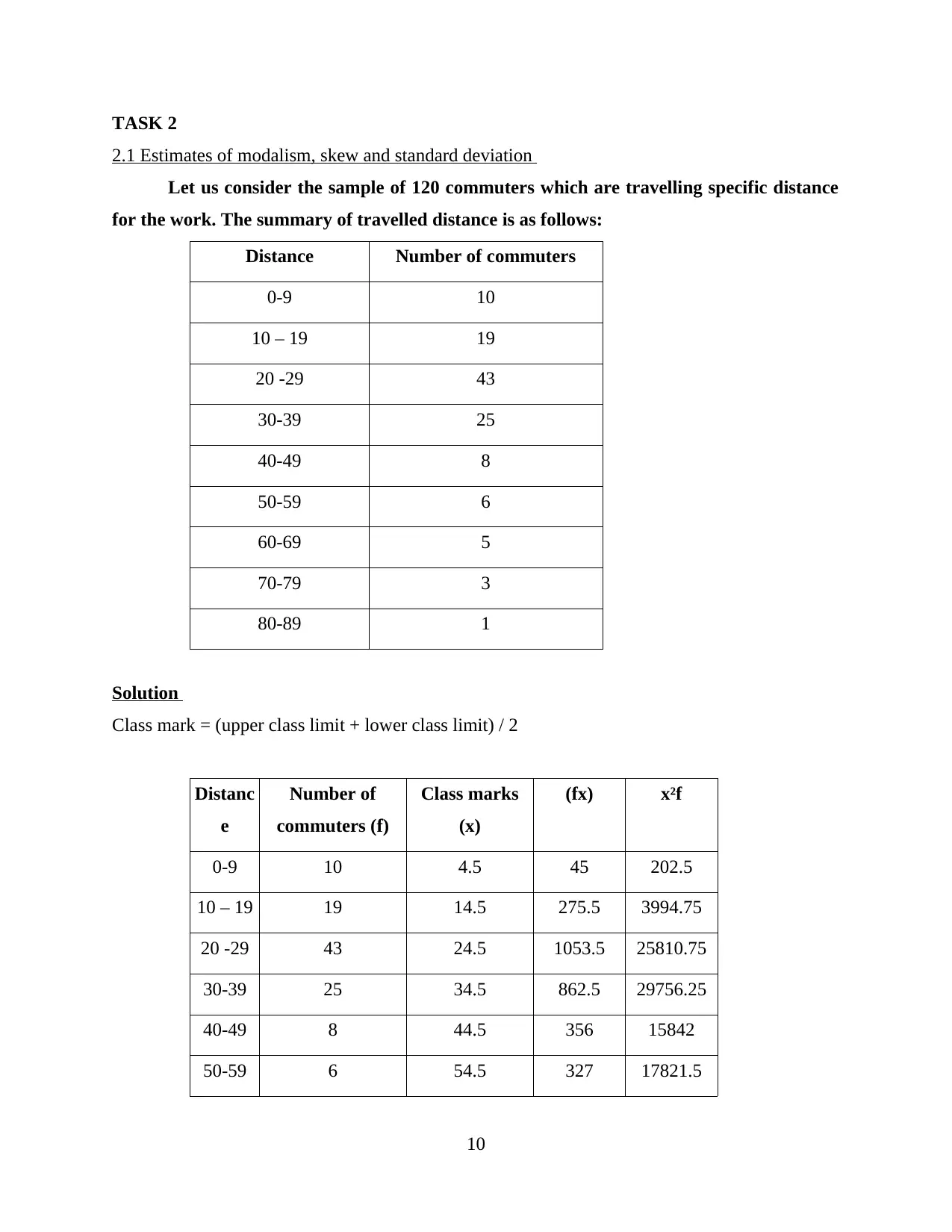
TASK 2
2.1 Estimates of modalism, skew and standard deviation
Let us consider the sample of 120 commuters which are travelling specific distance
for the work. The summary of travelled distance is as follows:
Distance Number of commuters
0-9 10
10 – 19 19
20 -29 43
30-39 25
40-49 8
50-59 6
60-69 5
70-79 3
80-89 1
Solution
Class mark = (upper class limit + lower class limit) / 2
Distanc
e
Number of
commuters (f)
Class marks
(x)
(fx) x²f
0-9 10 4.5 45 202.5
10 – 19 19 14.5 275.5 3994.75
20 -29 43 24.5 1053.5 25810.75
30-39 25 34.5 862.5 29756.25
40-49 8 44.5 356 15842
50-59 6 54.5 327 17821.5
10

60-69 5 64.5 322.5 20801.25
70-79 3 74.5 223.5 16650.75
80-89 1 84.5 84.5 7140.25
Sum 120 3550 138020
Mean = ∑ fx / ∑f
= 3550/120 = 29.58
(b) Mean = 25.58
The maximum class frequency of the given data is 43 and thus the corresponding modal class is
20-29.
The lower limit l of modal class = 20
class size (h) = 9
frequency of modal class = f1 = 43
frequency of class preceding modal class = f0 = 19
frequency of class succeding modal class = f2 = 25
Mode = l + [ (f1 – f0 )/ (2f1 – f0 -f2) ] *h
= 20 + [ (43 – 19 )/ (2(43) – 19 - 25) ] *9
Mode = 25.14
Variance = [∑x²f - (∑xf / N) ] / N
= [138020 – 29.58 ] / 120
Variance = 1149.92
Standard deviation = 33.91
Median= When the number of observations is odd formula is : Xm= (Xn+1)/ 2
When the number of observations is even formula is : Xm = (X n/2 + (Xn+2)/2)/2
In this case number of observations are 9.
X m= (9/2+ (9+2)/2)/2
= (4.5+5.5)/2
11

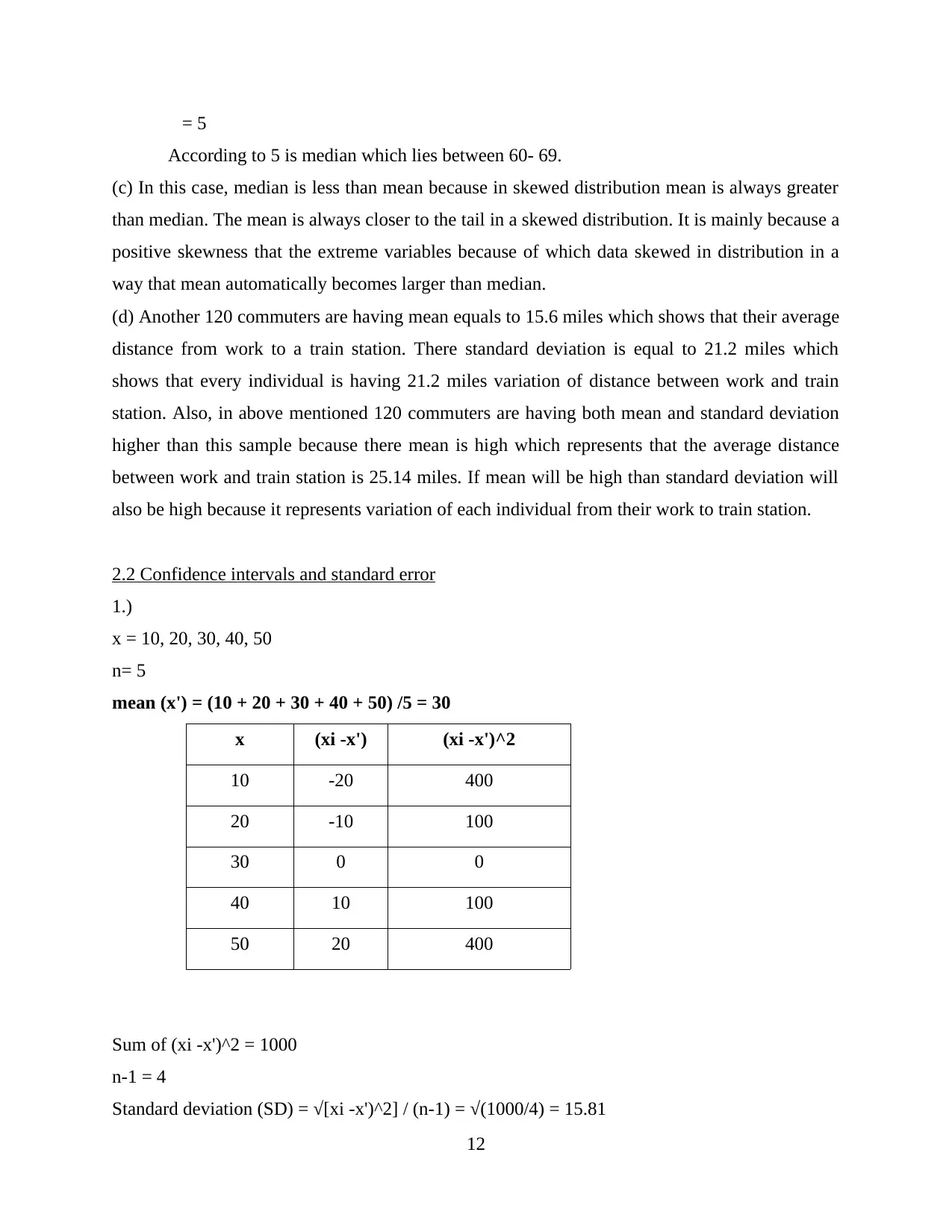
= 5
According to 5 is median which lies between 60- 69.
(c) In this case, median is less than mean because in skewed distribution mean is always greater
than median. The mean is always closer to the tail in a skewed distribution. It is mainly because a
positive skewness that the extreme variables because of which data skewed in distribution in a
way that mean automatically becomes larger than median.
(d) Another 120 commuters are having mean equals to 15.6 miles which shows that their average
distance from work to a train station. There standard deviation is equal to 21.2 miles which
shows that every individual is having 21.2 miles variation of distance between work and train
station. Also, in above mentioned 120 commuters are having both mean and standard deviation
higher than this sample because there mean is high which represents that the average distance
between work and train station is 25.14 miles. If mean will be high than standard deviation will
also be high because it represents variation of each individual from their work to train station.
2.2 Confidence intervals and standard error
1.)
x = 10, 20, 30, 40, 50
n= 5
mean (x') = (10 + 20 + 30 + 40 + 50) /5 = 30
x (xi -x') (xi -x')^2
10 -20 400
20 -10 100
30 0 0
40 10 100
50 20 400
Sum of (xi -x')^2 = 1000
n-1 = 4
Standard deviation (SD) = √[xi -x')^2] / (n-1) = √(1000/4) = 15.81
12

Standard error (SE) = SD / √n = 15.81 / √5 = 7.07
Standard error = 7.07
2.3 Implications of central limit theorem (CLT)
CLT is one of the significant theorem in the statistical analysis of the data values. It
allows understanding and prediction of the behaviour of estimated data values through repeated
sampling. The theorem describes the shape of the mean distribution when repeated samples from
a definite population are drawn. The theorem implies that when sample size is increased then
mean distribution tends to approach towards normality. One of the implication which makes
central limit theorem remarkable is that its results are valid irrespective of the distribution and
shape of original population. From the application of theorem it is also easy to demonstrate that
mean of the distribution is equals to mean of the population and variance can be calculated by
dividing variance of population by n. Thus, it can be concluded that when sample size is
increased and population variance reduces then the variance of distribution is also reduced.
2.4 Probability of statistics and interpretations of the results
Let us consider a sample data set of 25 students whose average grade is 9.2. The
average grade for another sample is 9.32. The average sample for 10 different samples,
with each sample size 25 is as follows:
Sample (n=25) Average
grade
1 10.12
2 9.2
3 9.68
4 9.52
5 9.16
6 9.2
7 9.88
8 9.12
13

9 9.36
10 8.84
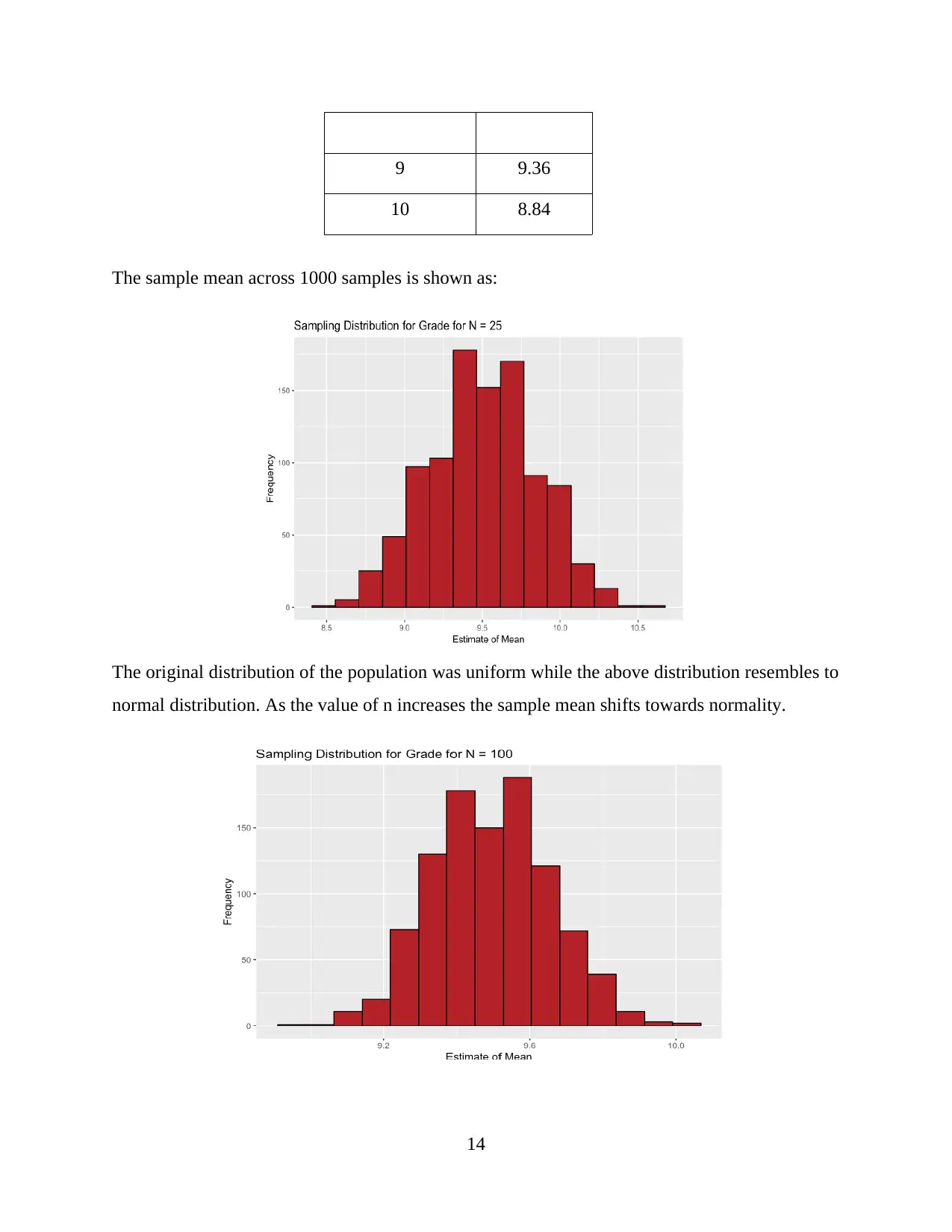
The sample mean across 1000 samples is shown as:
The original distribution of the population was uniform while the above distribution resembles to
normal distribution. As the value of n increases the sample mean shifts towards normality.
14

With increasing sample size difference between true population value and samples decreases and
estimation becomes more certain. The mean value of the curve is 9.4. Thus, the probability of
students scoring marks less than 9.4 is 0.5. Similarly, the probabilities can be determined by
using the area under curve. This can be done by using z values.
For instance the probability of students scoring at least 9.2 marks = 1 -[P (marks>9.2)].
The z value for the region can be calculated by using mean and standard deviation so that
probability or the area under curve can be determined.
Another example of data set is : Let the scores of test are distributed normally and have standard
deviation of 5.2 and average value of 80 then the probability of scores below 73 can be
calculated as:
mean = 80
standard deviation = 5.2
z = (73-80)/5.2 = -1.34
From the z score chart it is observed that the required probability is 0.0901 so the percentage is
9.01%
15

16

17

18

19

20

21