Vehicle Maths 3 - Assignment 3

This assignment covers solving simultaneous and quadratic equations in Vehicle Maths 3. It includes methods to solve simultaneous equations, formula for solving quadratic equations, and graphing quadratic equations.

Vehicle Maths
Level: 3 Unit Ref: M3 Assignment No:3
Unit Title: Vehicle Maths 3
Candidate
Name: Ref No:
INSTRUCTIONS FOR LEARNERS – PLEASE READ CAREFULLY
Ensure that your name and candidate number are written clearly on all your
answer sheets.
1. This assignment may be completed in your own handwriting or if you prefer you may use a
word- processor.
2. The standard of presentation, neatness and accuracy of your answers will be taken into
account when marking your work.
3. Your assessor will brief you about this assignment prior to starting.
4. To complete some aspects of the assignment you may need to refer to textbooks, vehicle
manufacturers’ data and workshop manuals.
5. Please show all your workings out in your answers.
6. Pass Mark is 60%. Each question has been given a pass mark that must be achieved.
This assignment forms part of your overall assessment for this unit and may be
shown to the external verifier when he/she visits your college or training
centre. Failure to present your assignment on time may affect the marks you
can achieve for your work.
Date of issue for this assignment:
Date for completion of this
assignment:
Important notes:
1. You should attempt all questions.
1 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

2. Please read each question carefully.
3. Ensure you write the number of each question on the left-hand side of your answer
sheet.
Assignment 3
1. This question is concerned with solving simultaneous and quadratic equations.
a. State TWO methods that can be used to solve simultaneous equations
(3.1) 2 marks
i. Graphical Method
ii. Elimination Method
b. Solve the following simultaneous equations: (3.1) 16 marks
i. 5x + 3y = 19
3x + 2y = 12
We multiply the first equation by 2 and the second equation by 3 to obtain:
2 ( 5 x +3 y=19 ) =10 x+ 6 y=38 …(equation3)
3 ( 3 x+2 y=12 )=9 x+ 6 y=36 …( equation 4)
Then, we subtract equation 4 from equation 3 to obtain,
( 10 x+ 6 y )− ( 9 x +6 y )=38−36
x=2
Substituting x=2 into the first equation we get,
5(2)+3 y=19
10+3 y=19
3 y=19−10=9
y= 9
3 =3
Therefore, x=2∧ y=3
2 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

ii. 3x + 4y = 29
8x - 2y = 14
We multiply the second equation by 2 to obtain
3 x+ 4 y =29 … equation1
2 ( 8 x−2 y=14 ) =16 x−4 y=28 …(equation3)
Then, we add equation 1 and 3 to get
( 3 x+4 y ) − ( 16 x−4 y ) =29+28
19 x=57
x= 57
19 =3
Substituting x=3 into the first equation we get,
3(3)+ 4 y=29
9+ 4 y=29
4 y=29−9=20
y= 20
4 =5
Therefore, x=3∧ y=5
3 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

iii. A person pays at a garage £50 for 30 litres of petrol and one litre of
oil. On the next visit they pay £45 for 20 litres of petrol and 2 litres
of oil. Assuming there have been no changes in the price, calculate
the price paid per litre of petrol and oil.
Let the price of petrol per litre be x and the price per litre of oil be y so that,
30 x+ y=£ 50 … equation 1
20 x+ 2 y =£ 4 5 … equation 2
Then, multiply the first equation to get
¿
60 x+2 y =100 … equation3
After that, we subtract equation 2 from equation 3. That is,
( 60 x+ 2 y ) − ( 20 x+2 y )=100−45
40 x=55
x= 55
40 = 11
8
Substituting x= 11
8 into equation 1 we get
30 ( 11
8 )+ y =50
4 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

y=50−30 ( 11
8 )=50− 165
4 =35
4
x= 11
8 , y= 35
4
Therefore, petrol costs x=£ 11
8 per litre whereas oil costs £ 35
4 per litre .
c. State the formula used for solving quadratic equations. (3.2) 2
marks
Given a quadratic equation in the form y=a x2 +bx +c , x=−b ± √b2−4 ac
2 a
d. Solve the following using the quadratic equation formula. (3.2) 8
marks
i. x2 - 4x = - 3
We rearrange the equation into the form y=a x2 +bx +c to get
x2−4 x+3=0 , a=1 ,b=−4 , c=3
Applying the quadratic formula
x=−b ± √ b2−4 ac
2 a
x= 4 ± √ (−4)2−4 ×1 ×3
2 ×1 = 4 ± √ 16−12
2 = 4 ± √ 4
2 = 4 ±2
2 =2 ± 1
x=2+1=3∨x=2−1=1
Therefore, x=3∨x=1
ii. x2 - 12x = -35
We rearrange the equation into the form y=a x2 +bx +c to get
x2−12 x+35=0 , a=1, b=−12 , c=35
5 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

Applying the quadratic formula
x=−b ± √ b2−4 ac
2 a
x= 12± √(−12)2−4 ×1 ×35
2 ×1 = 12± √ 144−140
2 =12 ± √4
2 = 12 ±2
2 =6 ± 1
x=6+ 1=7∨x=6−1=5
Therefore, x=7∨x=5
e. Draw a graph to find solution to the following quadratic equations:
(3.3) 20 marks
i. 6x2 - 7x - 5 = 0 (plot between x = -2 and x = 3)
x -2 -1 0 1 2 3
y 33 8 -5 -6 5 28
6 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

From the graph above, 6 x2−7 x−5=0 has the solutions x=−0.5∧x=1.667
7 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

ii. 2x2 - x - 6 = 0 (plot between x = -4 and x = 6)
x -4 -3 -2 -1 0 1 2 3 4 5 6
y 30 15 4 -3 -6 -5 0 9 22 39 60
8 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3

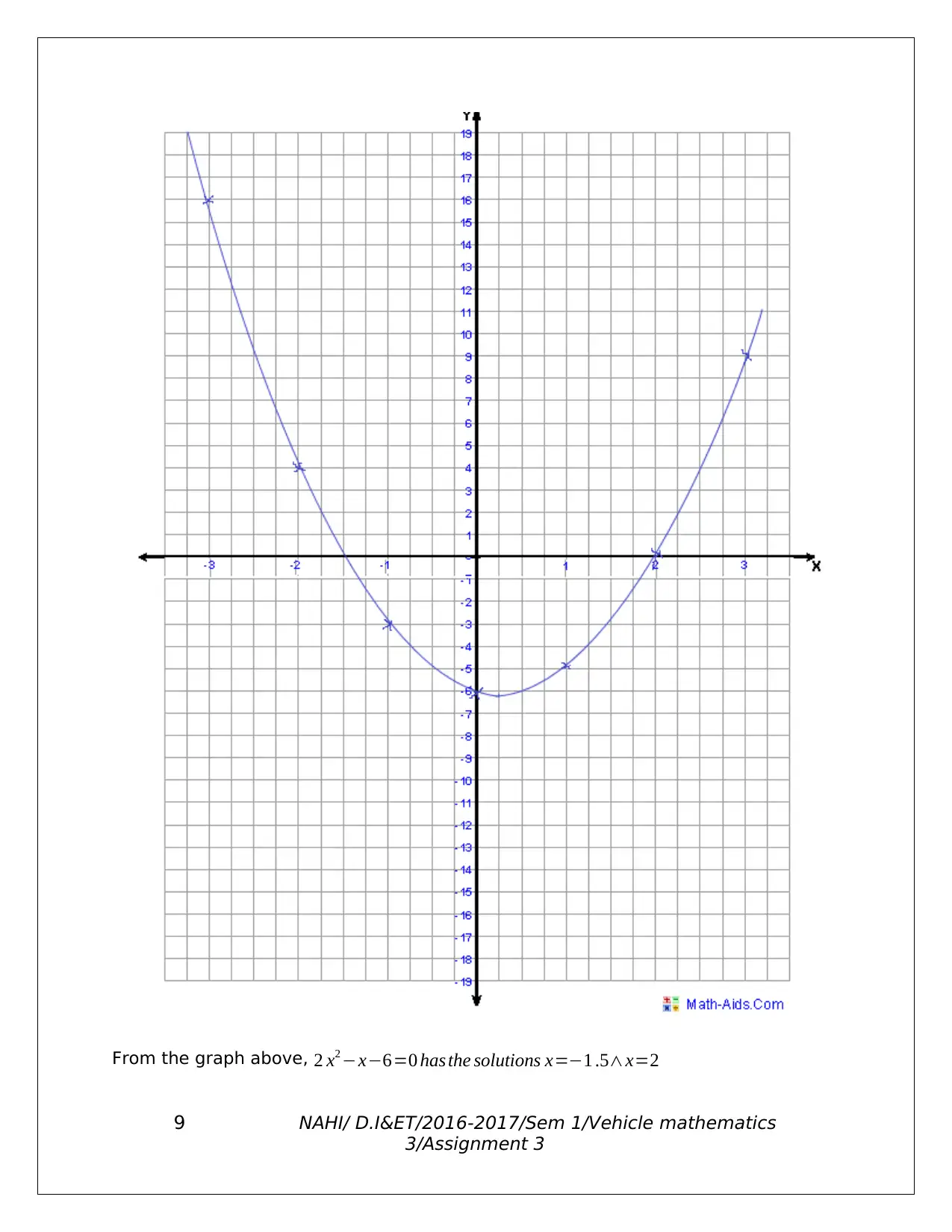
From the graph above, 2 x2 −x−6=0 has the solutions x=−1 .5∧x=2
9 NAHI/ D.I&ET/2016-2017/Sem 1/Vehicle mathematics
3/Assignment 3