Weighted Average Cost of Capital

This document provides a detailed explanation of the calculation of Weighted Average Cost of Capital (WACC) for Perfect Image NZ Ltd. It includes step-by-step calculations for determining the cost of equity, cost of debt, and cost of preference shares. The document also discusses the factors affecting the cost of capital and provides a comprehensive analysis of portfolio returns and risks.

WEIGHTED AVERAGE COST OF CAPITAL
SOLUTION 1
Project’s initial, (Year0) cash flows.
The project’s initial cash flow is the initial investment less net working capital less the lost
opportunity cost of the sale of land (after tax). i.e.
t=0
Initial (depreciable) investment -$ 265,000,000.00
CF due to change in net working
capital -$ 11,950,000.00
Opportunity cost of lost land sale
(after tax) -$ 11,250,000.00
-$ 288,200,000.00
SOLUTION 2
Weighted average cost of capital (WACC) of Perfect Image NZ Ltd
WACC = Cost of equity* Weight of Equity + Cost of debt* Weight of Debt*1- Corporate tax rate +
Cost of non-redeemable preference shares * Weight of preference shares (CFI, 2019).
Step 1: Cost of Equity
It is given that that Perfect image holds 18,000,000 ordinary shares selling for $38 per share.
Furthermore, the company pays regular dividends.
The cost of equity can be determined using the Dividend growth model formula
Re= D1/P0 + g
Where D1 = dividend paid for period, P0 = share price at the beginning and g = growth factor
(Investing Answers, 2019).
Perfect Image NZ made a dividend payment of $3.81 and the initial share price was $38. To
calculate the constant growth factor, we take the average growth rates across each dividend year
to get 2.59% (see appendix).
Thus, using the dividend growth model, the cost of equity is 12.6163% (3.81/38+2.59%).

Step 2: Cost of Debt
It is given that the company borrowed $150,000,000, 7.25% coupon bonds outstanding with 20
years to maturity redeemable at par, selling for 95 per cent of par; the bonds have a $1000 par
value each and make semi-annual coupon payments.
To calculate the cost of debt we need to determine the yield to maturity using the variables below.
n= 40
Market Value = 0.95*150,000,000= $142,500,000
Coupon Payment = 150,000,000*7.5%*6/12=5,625,000
Face Value=$150,000,000
142,500,000= 5625000
(1+ ytm /2)+ 5625000
(1+ ytm /2)2 + …..+ 155,625,000
¿ ¿
Solving the above equation gives a Yield to maturity of 8.005%. Hence, the cost of debt is given
as 8.01%. The corporate tax is given as 28% and will be applied to the cost of debt when
calculating WACC.
Step 3: Cost of Preference Shares
It is given that Perfect image holds 11,000,000 non-redeemable preference shares (par value $ 10
per share) with 6.5% dividends (after taxes), selling for $24 per share.
The cost of preference shares is given by formula below:-
Cost of preference shares = Dividend/market price of preference share (Efinance, 2019)
=6.5%*10/24
=2.7083%
Step 4: Weight of Debt, Equity and Preference shares
The market value of Equity (E) (both ordinary and preference) and the market value of Debt (D)
will be required to determine the Weights of Equity and Debt.
The market value of ordinary equity is the current share price, P0, multiplied by its shares
outstanding i.e.
Market Value (E) = 18, 0000, 0000*38 = $684,000,000

The market value of Non-redeemable Preference shares (P) is the current share price, P0,
multiplied by the number of shares outstanding i.e.
Market Value (P) = 11, 0000, 0000*24 = $264,000,000
The market value of Debt (D) is the current selling price at par, multiplied by the face value of the
bond i.e.
Market Value (D) =0.95*150,000,000= $142, 500, 0000
Weight of Debt, Wd= D/D+E+P = 13.07%
Weight of Equity, We= E/D+E+= 62.72%
Weight of Preference shares, Wp= P/D+E+P = 24.21%
,
Weighted Average Cost of Capital
WACC =Weight Debt * cost of debt *(1 – T) + Weight equity *cost of equity+ Weight Preference
shares *cost of Preference shares
Where T is the corporate tax given as 28% (CFI, 2019)
WACC =13.07%*8.01 %*( 1-28%) +62.72%*12.6163%+24.21%*2.7083%
WACC =9.3224%
The cost of capital for Perfect Image NZ is calculated as 9.32%.
SOLUTION 3
General assumptions
Initial (depreciable) investment $265,000,0
00
Diminishing value depriciation per year 25%
unit sales per year
385,000
variable costs $550
net working capital $11,950,00
0
Selling price per year $1,350
fixed cost p.a $225,000,0
00
Income tax rate 28%
Discount rate 9.32%
Salvage value $32,000,00
0
book sale $47,164,30
7

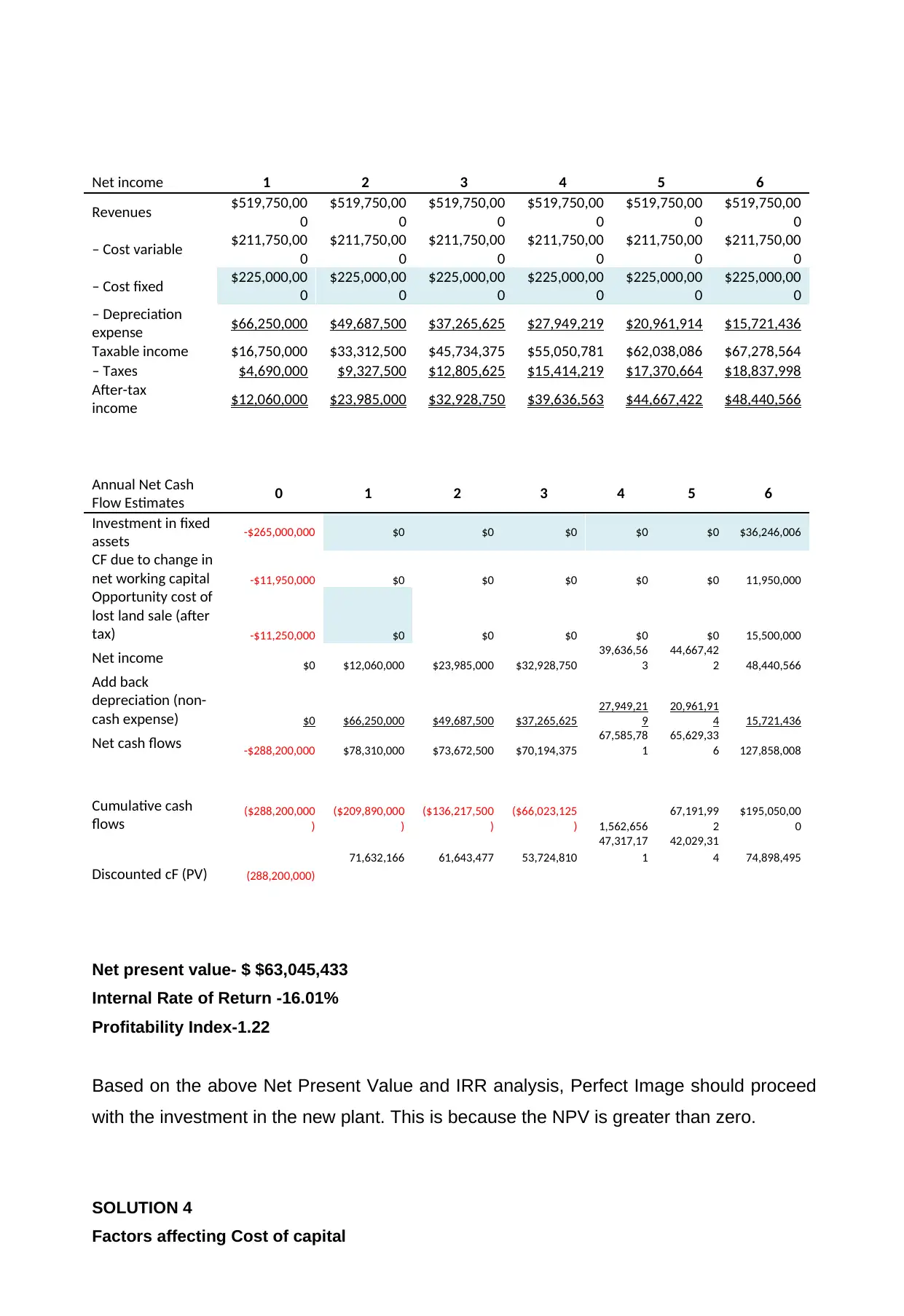
Net income 1 2 3 4 5 6
Revenues $519,750,00
0
$519,750,00
0
$519,750,00
0
$519,750,00
0
$519,750,00
0
$519,750,00
0
– Cost variable $211,750,00
0
$211,750,00
0
$211,750,00
0
$211,750,00
0
$211,750,00
0
$211,750,00
0
– Cost fixed $225,000,00
0
$225,000,00
0
$225,000,00
0
$225,000,00
0
$225,000,00
0
$225,000,00
0
– Depreciation
expense $66,250,000 $49,687,500 $37,265,625 $27,949,219 $20,961,914 $15,721,436
Taxable income $16,750,000 $33,312,500 $45,734,375 $55,050,781 $62,038,086 $67,278,564
– Taxes $4,690,000 $9,327,500 $12,805,625 $15,414,219 $17,370,664 $18,837,998
After-tax
income $12,060,000 $23,985,000 $32,928,750 $39,636,563 $44,667,422 $48,440,566
Annual Net Cash
Flow Estimates 0 1 2 3 4 5 6
Investment in fixed
assets -$265,000,000 $0 $0 $0 $0 $0 $36,246,006
CF due to change in
net working capital -$11,950,000 $0 $0 $0 $0 $0 11,950,000
Opportunity cost of
lost land sale (after
tax) -$11,250,000 $0 $0 $0 $0 $0 15,500,000
Net income $0 $12,060,000 $23,985,000 $32,928,750
39,636,56
3
44,667,42
2 48,440,566
Add back
depreciation (non-
cash expense) $0 $66,250,000 $49,687,500 $37,265,625
27,949,21
9
20,961,91
4 15,721,436
Net cash flows -$288,200,000 $78,310,000 $73,672,500 $70,194,375
67,585,78
1
65,629,33
6 127,858,008
Cumulative cash
flows ($288,200,000
)
($209,890,000
)
($136,217,500
)
($66,023,125
) 1,562,656
67,191,99
2
$195,050,00
0
Discounted cF (PV) (288,200,000)
71,632,166 61,643,477 53,724,810
47,317,17
1
42,029,31
4 74,898,495
Net present value- $ $63,045,433
Internal Rate of Return -16.01%
Profitability Index-1.22
Based on the above Net Present Value and IRR analysis, Perfect Image should proceed
with the investment in the new plant. This is because the NPV is greater than zero.
SOLUTION 4
Factors affecting Cost of capital

 Market opportunities-Increased market opportunities increase the need for capital by
organizations, which in turn increase the cost of capital (EFINANCE, 2019).
 Risk- An investor would require a higher cost of capital for projects that are considered
riskier than others. This higher cost will be commensurate with the level of risk taken. In
other words, riskier projects have a higher cost of capital (EFINANCE, 2019).
 Dividend policy- If a company retains more of its profits or does not declare dividends
regularly, then it will be adding capital to the cost of equity. This will affect the cost of
capital (EFINANCE, 2019).
 Capital Structure- The capital structure policy of a company will affect its cost of capital as
these have an effect on the weights (EFINANCE, 2019).

PORTFOLIO ANALYSIS
SOLUTION 1
The table below shows the average monthly return, the standard deviation, and variance for each
of the companies. The data used was the 60 month returns data as shown in the appendix and
Excel functions “Variance P” and “Standard Deviation P.”
SKC (A) WHS (B) AIA (C) HLG (D)
average return 0.61% -0.07% 1.46% 1.01%
standard deviation 0.0550 0.0441 0.0512 0.0795
Variance 0.0030 0.0019 0.0026 0.0063
SOLUTION 2
The table below shows the covariance between securities A and B; B and C; A and C; C and D; A
and D and B and D. The data used was the 60 month returns data as shown in the appendix and
Excel functions “COVARIANCE P.”
Portfolio
Covarianc
e
A and B 0.0626%
B and C 0.0279%
A and C 0.1076%
C and D 0.0169%
A and D 0.0482%
B and D 0.0789%
Question 3
The table below shows the portfolio returns and risks between securities A and B; B and C; A and
C; C and D; A and D and B and D. The formula used is as below:-
Portfolio Return = w1r1+w2r2
Portfolio Variance = (w(1)^2 x o(1)^2) + (w(2)^2 x o(2)^2) + (2 x (w(1)w(2)cov(1,2))
Standard deviation= sqrt (variance)
Where
w1 = the portfolio weight of the first asset
w2= the portfolio weight of the second asset
r1 = return of the first asset
r2 = return of the second asset
cov(1,2) = covariance of first asset and second asset

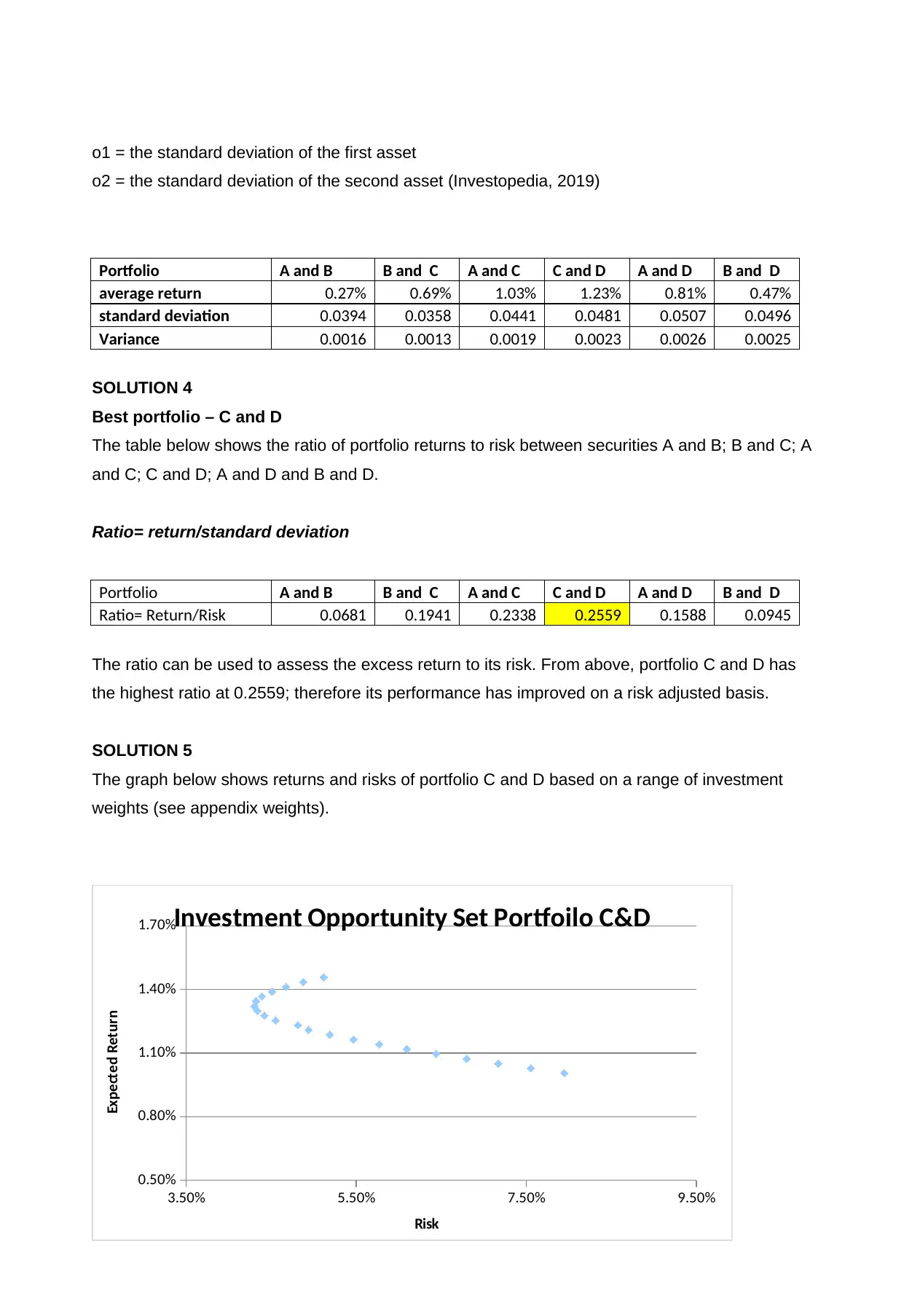
o1 = the standard deviation of the first asset
o2 = the standard deviation of the second asset (Investopedia, 2019)
Portfolio A and B B and C A and C C and D A and D B and D
average return 0.27% 0.69% 1.03% 1.23% 0.81% 0.47%
standard deviation 0.0394 0.0358 0.0441 0.0481 0.0507 0.0496
Variance 0.0016 0.0013 0.0019 0.0023 0.0026 0.0025
SOLUTION 4
Best portfolio – C and D
The table below shows the ratio of portfolio returns to risk between securities A and B; B and C; A
and C; C and D; A and D and B and D.
Ratio= return/standard deviation
Portfolio A and B B and C A and C C and D A and D B and D
Ratio= Return/Risk 0.0681 0.1941 0.2338 0.2559 0.1588 0.0945
The ratio can be used to assess the excess return to its risk. From above, portfolio C and D has
the highest ratio at 0.2559; therefore its performance has improved on a risk adjusted basis.
SOLUTION 5
The graph below shows returns and risks of portfolio C and D based on a range of investment
weights (see appendix weights).
3.50% 5.50% 7.50% 9.50%
0.50%
0.80%
1.10%
1.40%
1.70%Investment Opportunity Set Portfoilo C&D
Risk
Expected Return

The efficient frontier is the region in the graph where the portfolio expected returns are above
1.32%. This is the point where the portfolio offers the highest returns for the minimum level of risk
at 4.39%.
That is at weights of 75% invested stock AIA and 25% invested in stock D (HLG, the portfolio will
be at minimum risk of 4.39%. Therefore, an investor should invest in a portfolio with increasing
weights of stock C (AIA).
SOLUTION 6
Betas
The table below shows the betas for the four securities. The beta was calculated by regressing
the returns of each of the company on the returns for the S&P/NZX50 Index
SKC WHS AIA HLG NZ50
Beta 1.3461 0.3666 1.1971 0.6586 1.0000
A beta coefficient is a measure of the volatility in comparison to the unsystematic risk of the entire
market. A beta <1.0 means that the security is less volatile than the market. A beta >1.0 means
that the security is more volatile than the market. The amount of Debt will affect a company’s beta.
The industry the company is in may also affect the beta of the stock (Investopedia, 2019).

REFERENCES
CFI, 2019. Definition of WACC. [Online]
Available at: https://corporatefinanceinstitute.com/resources/knowledge/finance/what-is-wacc-formula/
Efinance, 2019. Cost of Preference Share Capital. [Online]
Available at: https://efinancemanagement.com/investment-decisions/cost-of-preference-share-capital
EFINANCE, 2019. Factors Affecting Cost of Capital. [Online]
Available at: https://efinancemanagement.com/investment-decisions/factors-affecting-cost-of-capital
Investing Answers, 2019. Gordon Growth Model. [Online]
Available at: https://investinganswers.com/financial-dictionary/income-dividends/gordon-growth-model-
5270
Investopedia, 2019. How can I Measure Portfolio Variance?. [Online]
Available at: https://www.investopedia.com/ask/answers/071515/how-can-i-measure-portfolio-
variance.asp
Investopedia, 2019. What Beta Means When Considering a Stock's Risk. [Online]
Available at: https://www.investopedia.com/investing/beta-know-risk/

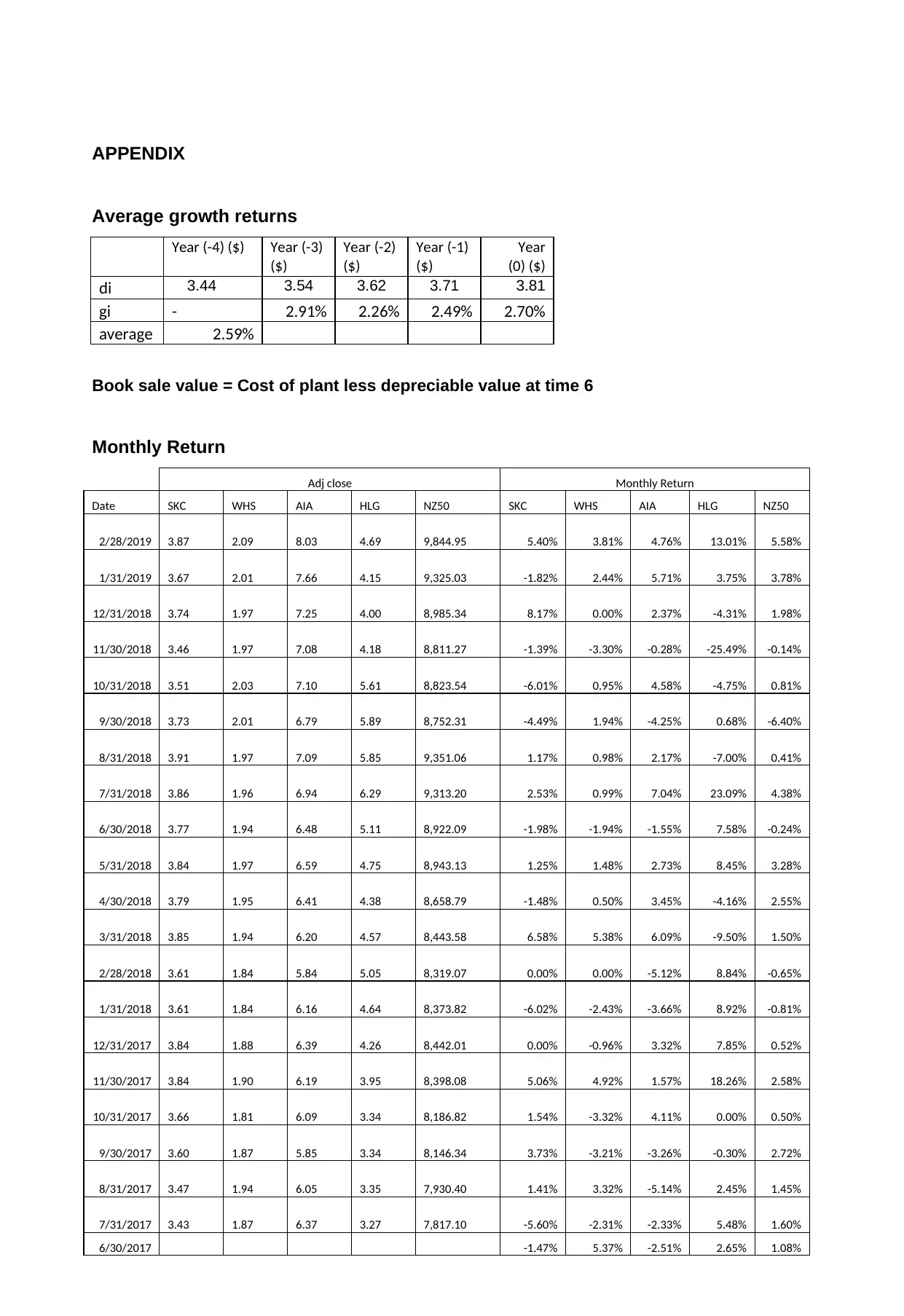
APPENDIX
Average growth returns
Year (-4) ($) Year (-3)
($)
Year (-2)
($)
Year (-1)
($)
Year
(0) ($)
di 3.44 3.54 3.62 3.71 3.81
gi - 2.91% 2.26% 2.49% 2.70%
average 2.59%
Book sale value = Cost of plant less depreciable value at time 6
Monthly Return
Adj close Monthly Return
Date SKC WHS AIA HLG NZ50 SKC WHS AIA HLG NZ50
2/28/2019 3.87 2.09 8.03 4.69 9,844.95 5.40% 3.81% 4.76% 13.01% 5.58%
1/31/2019 3.67 2.01 7.66 4.15 9,325.03 -1.82% 2.44% 5.71% 3.75% 3.78%
12/31/2018 3.74 1.97 7.25 4.00 8,985.34 8.17% 0.00% 2.37% -4.31% 1.98%
11/30/2018 3.46 1.97 7.08 4.18 8,811.27 -1.39% -3.30% -0.28% -25.49% -0.14%
10/31/2018 3.51 2.03 7.10 5.61 8,823.54 -6.01% 0.95% 4.58% -4.75% 0.81%
9/30/2018 3.73 2.01 6.79 5.89 8,752.31 -4.49% 1.94% -4.25% 0.68% -6.40%
8/31/2018 3.91 1.97 7.09 5.85 9,351.06 1.17% 0.98% 2.17% -7.00% 0.41%
7/31/2018 3.86 1.96 6.94 6.29 9,313.20 2.53% 0.99% 7.04% 23.09% 4.38%
6/30/2018 3.77 1.94 6.48 5.11 8,922.09 -1.98% -1.94% -1.55% 7.58% -0.24%
5/31/2018 3.84 1.97 6.59 4.75 8,943.13 1.25% 1.48% 2.73% 8.45% 3.28%
4/30/2018 3.79 1.95 6.41 4.38 8,658.79 -1.48% 0.50% 3.45% -4.16% 2.55%
3/31/2018 3.85 1.94 6.20 4.57 8,443.58 6.58% 5.38% 6.09% -9.50% 1.50%
2/28/2018 3.61 1.84 5.84 5.05 8,319.07 0.00% 0.00% -5.12% 8.84% -0.65%
1/31/2018 3.61 1.84 6.16 4.64 8,373.82 -6.02% -2.43% -3.66% 8.92% -0.81%
12/31/2017 3.84 1.88 6.39 4.26 8,442.01 0.00% -0.96% 3.32% 7.85% 0.52%
11/30/2017 3.84 1.90 6.19 3.95 8,398.08 5.06% 4.92% 1.57% 18.26% 2.58%
10/31/2017 3.66 1.81 6.09 3.34 8,186.82 1.54% -3.32% 4.11% 0.00% 0.50%
9/30/2017 3.60 1.87 5.85 3.34 8,146.34 3.73% -3.21% -3.26% -0.30% 2.72%
8/31/2017 3.47 1.94 6.05 3.35 7,930.40 1.41% 3.32% -5.14% 2.45% 1.45%
7/31/2017 3.43 1.87 6.37 3.27 7,817.10 -5.60% -2.31% -2.33% 5.48% 1.60%
6/30/2017 -1.47% 5.37% -2.51% 2.65% 1.08%

3.63 1.92 6.53 3.10 7,693.99
5/31/2017 3.68 1.82 6.69 3.02 7,611.44 -6.85% 0.00% 2.00% -0.66% 2.60%
4/30/2017 3.95 1.82 6.56 3.04 7,418.90 0.46% -2.84% 1.30% -5.88% 0.54%
3/31/2017 3.94 1.87 6.48 3.23 7,378.75 7.70% -4.69% 3.54% -9.01% 2.53%
2/28/2017 3.65 1.97 6.26 3.55 7,196.78 0.73% -10.47% -7.90% 6.29% 0.41%
1/31/2017 3.63 2.20 6.79 3.34 7,167.46 8.99% -1.53% 7.31% 3.41% 1.66%
12/31/2016 3.33 2.23 6.33 3.23 7,050.75 -3.82% -8.07% 11.76% 5.90% 2.46%
11/30/2016 3.46 2.43 5.66 3.05 6,881.22 -0.51% -1.06% -0.57% 3.04% -0.23%
10/31/2016 3.48 2.45 5.70 2.96 6,896.95 1.28% -2.33% -6.60% -1.00% -0.92%
9/30/2016 3.43 2.51 6.10 2.99 6,960.68 -13.02% 2.39% -9.19% -1.97% -5.44%
8/31/2016 3.95 2.45 6.72 3.05 7,361.09 -8.58% 1.38% -2.00% 8.16% -0.51%
7/31/2016 4.32 2.42 6.85 2.82 7,398.83 -1.18% 3.21% 1.63% 7.63% 0.69%
6/30/2016 4.37 2.34 6.74 2.62 7,348.13 10.70% 1.08% 13.54% -1.13% 6.53%
5/31/2016 3.95 2.32 5.94 2.65 6,897.53 -5.18% 2.59% 4.17% -2.57% -2.02%
4/30/2016 4.16 2.26 5.70 2.72 7,039.42 -0.12% 1.68% 1.46% -5.56% 3.21%
3/31/2016 4.17 2.22 5.62 2.88 6,820.58 0.01% -4.83% -3.11% -5.57% 1.01%
2/29/2016 4.17 2.34 5.80 3.05 6,752.42 12.08% 8.21% 5.41% 5.17% 8.37%
1/31/2016 3.72 2.16 5.50 2.90 6,230.87 -4.28% 0.00% 9.91% -11.85% 0.98%
12/31/2015 3.89 2.16 5.01 3.29 6,170.22 5.42% 0.37% -3.48% -1.79% -2.44%
11/30/2015 3.69 2.15 5.19 3.35 6,324.26 5.48% 6.25% 8.90% 1.52% 3.67%
10/31/2015 3.50 2.02 4.76 3.30 6,100.15 4.74% -6.23% 0.38% -12.00% 1.90%
9/30/2015 3.34 2.16 4.75 3.75 5,986.37 10.06% 9.20% 9.38% 6.84% 7.03%
8/31/2015 3.03 1.98 4.34 3.51 5,593.36 -3.61% -3.85% -1.41% 6.36% -0.74%
7/31/2015 3.15 2.06 4.40 3.30 5,634.94 -12.22% 1.17% -8.50% -0.60% -4.83%
6/30/2015 3.58 2.03 4.81 3.32 5,920.96 5.24% -1.91% 9.63% -0.90% 3.39%
5/31/2015 3.41 2.07 4.39 3.35 5,726.96 -5.19% -9.03% 1.75% -8.22% -2.02%
4/30/2015 3.59 2.28 4.31 3.65 5,844.95 5.48% 2.86% 5.21% 4.89% 0.93%
3/31/2015 3.41 2.21 4.10 3.48 5,791.34 4.99% 9.50% 4.13% 0.87% -0.73%
2/28/2015 3.24 2.02 3.94 3.45 5,833.99 2.76% -2.21% 3.45% 6.15% -0.76%
1/31/2015 3.16 2.07 3.80 3.25 5,878.47 1.53% -4.56% -2.25% -3.27% 2.34%
12/31/2014 3.11 2.17 3.89 3.36 5,744.00 1.29% -8.06% 5.20% 8.39% 3.16%
11/30/2014 -1.27% 1.92% 9.30% -1.59% 2.65%

3.07 2.36 3.70 3.10 5,568.28
10/31/2014 3.11 2.31 3.38 3.15 5,424.45 0.51% 0.00% 1.85% -4.55% 0.68%
9/30/2014 3.09 2.31 3.32 3.30 5,387.83 10.11% 1.31% 0.52% 2.80% 2.53%
8/31/2014 2.81 2.28 3.31 3.21 5,255.04 -3.44% -1.29% 4.90% 14.64% 0.61%
7/31/2014 2.91 2.31 3.15 2.80 5,223.30 0.53% -2.21% -3.93% -7.59% 1.07%
6/30/2014 2.89 2.36 3.28 3.03 5,167.99 -5.53% 2.26% -2.05% -0.66% 0.52%
5/31/2014 3.06 2.31 3.35 3.05 5,141.48 -0.50% -10.14% 1.04% -3.17% -0.71%
4/30/2014 3.08 2.57 3.31 3.15 5,178.44 -5.44% 1.77% -2.77% -9.22% -1.04%
3/31/2014 3.26 2.53 3.41 3.47 5,232.68 10.45% 9.41% -6.22% 11.58% 1.80%
2/28/2014 2.95 2.31 3.64 3.11 5,139.98
Index Returns
Adj close Monthly Return
Date NZ50 NZ50
2/28/2019 9,844.95 5.58%
1/31/2019 9,325.03 3.78%
12/31/2018 8,985.34 1.98%
11/30/2018 8,811.27 -0.14%
10/31/2018 8,823.54 0.81%
9/30/2018 8,752.31 -6.40%
8/31/2018 9,351.06 0.41%
7/31/2018 9,313.20 4.38%
6/30/2018 8,922.09 -0.24%
5/31/2018 8,943.13 3.28%
4/30/2018 8,658.79 2.55%
3/31/2018 8,443.58 1.50%
2/28/2018 8,319.07 -0.65%
1/31/2018 8,373.82 -0.81%
12/31/2017 8,442.01 0.52%
11/30/2017 8,398.08 2.58%
10/31/2017 8,186.82 0.50%
9/30/2017 8,146.34 2.72%
8/31/2017 7,930.40 1.45%
7/31/2017 7,817.10 1.60%
6/30/2017 7,693.99 1.08%
5/31/2017 7,611.44 2.60%
4/30/2017 7,418.90 0.54%
3/31/2017 7,378.75 2.53%
2/28/2017 7,196.78 0.41%
1/31/2017 7,167.46 1.66%
12/31/2016 7,050.75 2.46%
11/30/2016 6,881.22 -0.23%
10/31/2016 6,896.95 -0.92%

9/30/2016 6,960.68 -5.44%
8/31/2016 7,361.09 -0.51%
7/31/2016 7,398.83 0.69%
6/30/2016 7,348.13 6.53%
5/31/2016 6,897.53 -2.02%
4/30/2016 7,039.42 3.21%
3/31/2016 6,820.58 1.01%
2/29/2016 6,752.42 8.37%
1/31/2016 6,230.87 0.98%
12/31/2015 6,170.22 -2.44%
11/30/2015 6,324.26 3.67%
10/31/2015 6,100.15 1.90%
9/30/2015 5,986.37 7.03%
8/31/2015 5,593.36 -0.74%
7/31/2015 5,634.94 -4.83%
6/30/2015 5,920.96 3.39%
5/31/2015 5,726.96 -2.02%
4/30/2015 5,844.95 0.93%
3/31/2015 5,791.34 -0.73%
2/28/2015 5,833.99 -0.76%
1/31/2015 5,878.47 2.34%
12/31/2014 5,744.00 3.16%
11/30/2014 5,568.28 2.65%
10/31/2014 5,424.45 0.68%
9/30/2014 5,387.83 2.53%
8/31/2014 5,255.04 0.61%
7/31/2014 5,223.30 1.07%
6/30/2014 5,167.99 0.52%
5/31/2014 5,141.48 -0.71%
4/30/2014 5,178.44 -1.04%
3/31/2014 5,232.68 1.80%
2/28/2014 5,139.98
1/31/2014
Portfolio weights C and D
portfolio
weight of c
portfolio
weight of d
expected return
of the portfolio
standard deviation
of the portfolio
100% 0% 1.46% 5.12%
95% 5% 1.44% 4.89%
90% 10% 1.41% 4.71%
85% 15% 1.39% 4.56%
80% 20% 1.37% 4.45%

75% 25% 1.35% 4.39%
70% 30% 1.32% 4.38%
65% 35% 1.30% 4.42%
60% 40% 1.28% 4.51%
55% 45% 1.25% 4.64%
50% 50% 1.23% 4.81%
45% 55% 1.21% 5.02%
40% 60% 1.19% 5.27%
35% 65% 1.16% 5.54%
30% 70% 1.14% 5.83%
25% 75% 1.12% 6.15%
20% 80% 1.10% 6.48%
15% 85% 1.07% 6.83%
10% 90% 1.05% 7.19%
5% 95% 1.03% 7.56%
0% 100% 1.01% 7.95%