What Is Business Statistics and Why Does
VerifiedAdded on 2022/09/09
|11
|1499
|13
AI Summary
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

NAME: ______________________________________
STUDENT NUMBER:__________________________
Math 20000D – Business Statistics
TERM TEST 2: 30 Marks Available (5% of Final Grade) Winter 2020
Instructions:
Unless noted otherwise,
round all percentages to two decimal places
round all other figures to at least four decimal places
If your final answer is incorrect you will need to show/explain your work in order to get partial
marks. (Use the space provided. You can use the back of the test sheets also.)
Calculators and Excel are permitted.
Data for test is available on Slate (TERMTESTDATA2)
Copies of Solutions are to be submitted in the dropbox Week 13
Questions start on next page
Page 1 of 11
STUDENT NUMBER:__________________________
Math 20000D – Business Statistics
TERM TEST 2: 30 Marks Available (5% of Final Grade) Winter 2020
Instructions:
Unless noted otherwise,
round all percentages to two decimal places
round all other figures to at least four decimal places
If your final answer is incorrect you will need to show/explain your work in order to get partial
marks. (Use the space provided. You can use the back of the test sheets also.)
Calculators and Excel are permitted.
Data for test is available on Slate (TERMTESTDATA2)
Copies of Solutions are to be submitted in the dropbox Week 13
Questions start on next page
Page 1 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

1) Hypothesis test (2 sample) (6 marks)
A developer wants to know if the houses in two different neighborhoods were built at roughly
the same time. He takes a random sample of houses from each neighborhood and finds the
summary statistics for the two shown in the table below:
At α=0 . 01 , test the claim that there is no significant difference between the average age of the
houses
Neighborhood Sample mean
x Population standard deviation
σ
Sample size
n
1 57.2 yrs 7.51 yrs 30
2 47.6 yrs 7.85 yrs 35
HINT: use test statistic
z= ( x1−x2 )− ( μ1−μ2 )
√ σ1
2
n1
+ σ 2
2
n2
.
Solution:
Null hypothesis: There is a significant difference between the average ages of the houses.
Alternative hypothesis: There is a significant difference between the average ages of the houses.
Page 2 of 11
A developer wants to know if the houses in two different neighborhoods were built at roughly
the same time. He takes a random sample of houses from each neighborhood and finds the
summary statistics for the two shown in the table below:
At α=0 . 01 , test the claim that there is no significant difference between the average age of the
houses
Neighborhood Sample mean
x Population standard deviation
σ
Sample size
n
1 57.2 yrs 7.51 yrs 30
2 47.6 yrs 7.85 yrs 35
HINT: use test statistic
z= ( x1−x2 )− ( μ1−μ2 )
√ σ1
2
n1
+ σ 2
2
n2
.
Solution:
Null hypothesis: There is a significant difference between the average ages of the houses.
Alternative hypothesis: There is a significant difference between the average ages of the houses.
Page 2 of 11

Test statistic (Z) = 5.0313
Alpha = 0.01
P-value = 0.0000
It is clear that P-value < alpha. Hence the null hypothesis is significant. Therefore it may
be summarized that there is a significant difference between the average ages of the houses.
Page 3 of 11
Alpha = 0.01
P-value = 0.0000
It is clear that P-value < alpha. Hence the null hypothesis is significant. Therefore it may
be summarized that there is a significant difference between the average ages of the houses.
Page 3 of 11
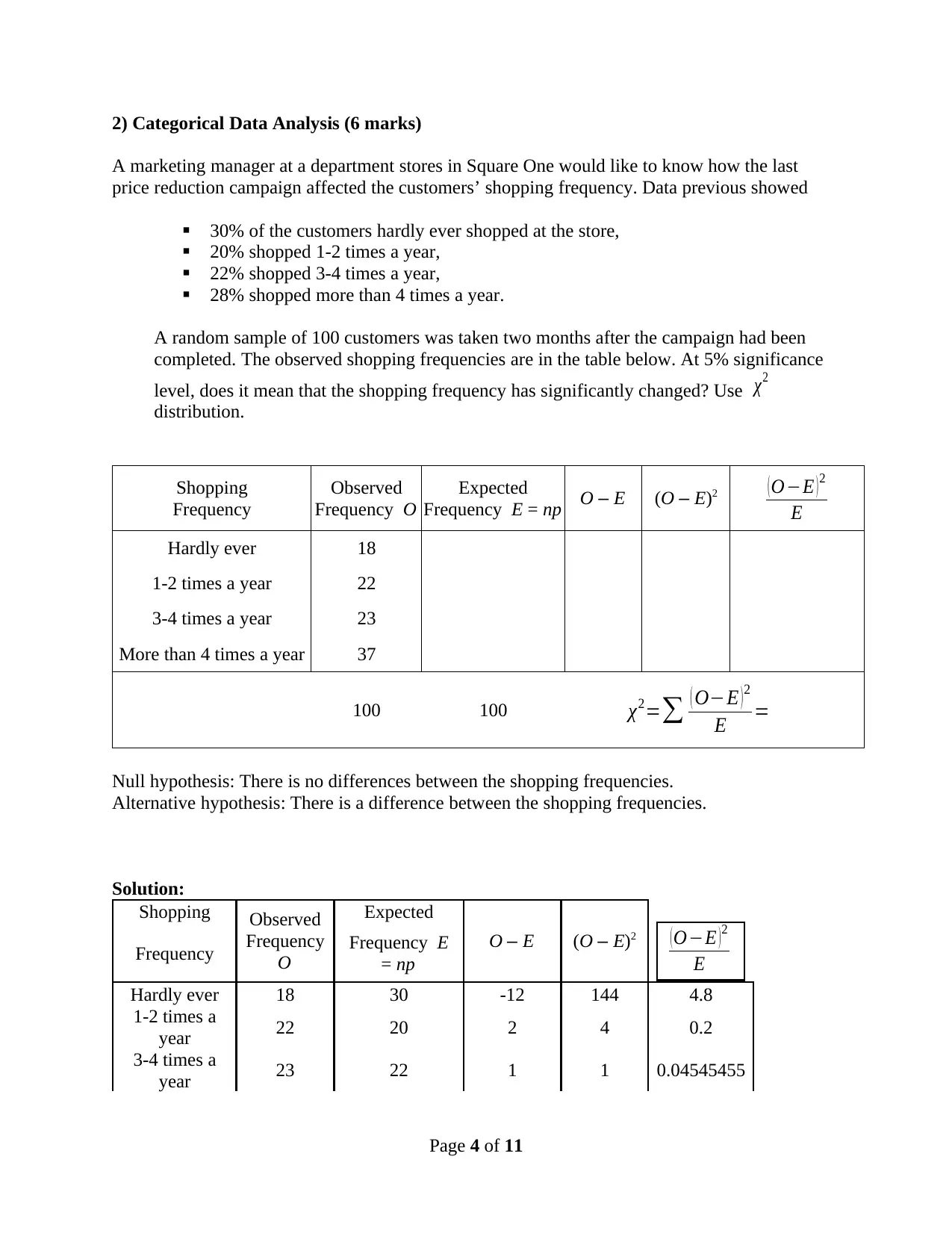
2) Categorical Data Analysis (6 marks)
A marketing manager at a department stores in Square One would like to know how the last
price reduction campaign affected the customers’ shopping frequency. Data previous showed
30% of the customers hardly ever shopped at the store,
20% shopped 1-2 times a year,
22% shopped 3-4 times a year,
28% shopped more than 4 times a year.
A random sample of 100 customers was taken two months after the campaign had been
completed. The observed shopping frequencies are in the table below. At 5% significance
level, does it mean that the shopping frequency has significantly changed? Use χ2
distribution.
Shopping
Frequency
Observed
Frequency O
Expected
Frequency E = np O – E (O – E)2 ( O−E ) 2
E
Hardly ever 18
1-2 times a year 22
3-4 times a year 23
More than 4 times a year 37
100 100 χ2=∑ ( O−E ) 2
E =
Null hypothesis: There is no differences between the shopping frequencies.
Alternative hypothesis: There is a difference between the shopping frequencies.
Solution:
Shopping Observed
Frequency
O
Expected
O – E (O – E)2 ( O−E ) 2
E
Frequency Frequency E
= np
Hardly ever 18 30 -12 144 4.8
1-2 times a
year 22 20 2 4 0.2
3-4 times a
year 23 22 1 1 0.04545455
Page 4 of 11
A marketing manager at a department stores in Square One would like to know how the last
price reduction campaign affected the customers’ shopping frequency. Data previous showed
30% of the customers hardly ever shopped at the store,
20% shopped 1-2 times a year,
22% shopped 3-4 times a year,
28% shopped more than 4 times a year.
A random sample of 100 customers was taken two months after the campaign had been
completed. The observed shopping frequencies are in the table below. At 5% significance
level, does it mean that the shopping frequency has significantly changed? Use χ2
distribution.
Shopping
Frequency
Observed
Frequency O
Expected
Frequency E = np O – E (O – E)2 ( O−E ) 2
E
Hardly ever 18
1-2 times a year 22
3-4 times a year 23
More than 4 times a year 37
100 100 χ2=∑ ( O−E ) 2
E =
Null hypothesis: There is no differences between the shopping frequencies.
Alternative hypothesis: There is a difference between the shopping frequencies.
Solution:
Shopping Observed
Frequency
O
Expected
O – E (O – E)2 ( O−E ) 2
E
Frequency Frequency E
= np
Hardly ever 18 30 -12 144 4.8
1-2 times a
year 22 20 2 4 0.2
3-4 times a
year 23 22 1 1 0.04545455
Page 4 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.
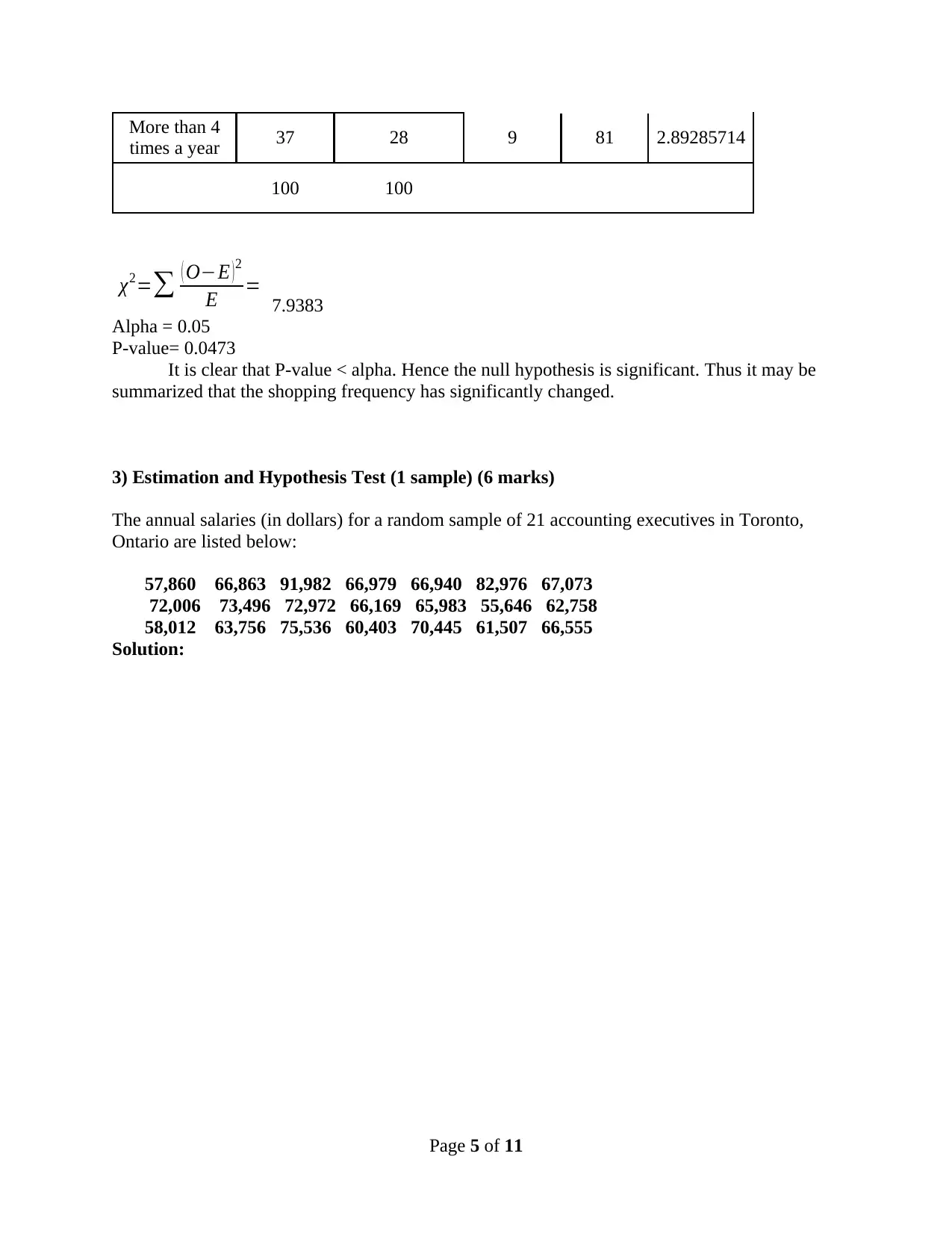
More than 4
times a year 37 28 9 81 2.89285714
100 100
χ2=∑ ( O−E ) 2
E = 7.9383
Alpha = 0.05
P-value= 0.0473
It is clear that P-value < alpha. Hence the null hypothesis is significant. Thus it may be
summarized that the shopping frequency has significantly changed.
3) Estimation and Hypothesis Test (1 sample) (6 marks)
The annual salaries (in dollars) for a random sample of 21 accounting executives in Toronto,
Ontario are listed below:
57,860 66,863 91,982 66,979 66,940 82,976 67,073
72,006 73,496 72,972 66,169 65,983 55,646 62,758
58,012 63,756 75,536 60,403 70,445 61,507 66,555
Solution:
Page 5 of 11
times a year 37 28 9 81 2.89285714
100 100
χ2=∑ ( O−E ) 2
E = 7.9383
Alpha = 0.05
P-value= 0.0473
It is clear that P-value < alpha. Hence the null hypothesis is significant. Thus it may be
summarized that the shopping frequency has significantly changed.
3) Estimation and Hypothesis Test (1 sample) (6 marks)
The annual salaries (in dollars) for a random sample of 21 accounting executives in Toronto,
Ontario are listed below:
57,860 66,863 91,982 66,979 66,940 82,976 67,073
72,006 73,496 72,972 66,169 65,983 55,646 62,758
58,012 63,756 75,536 60,403 70,445 61,507 66,555
Solution:
Page 5 of 11
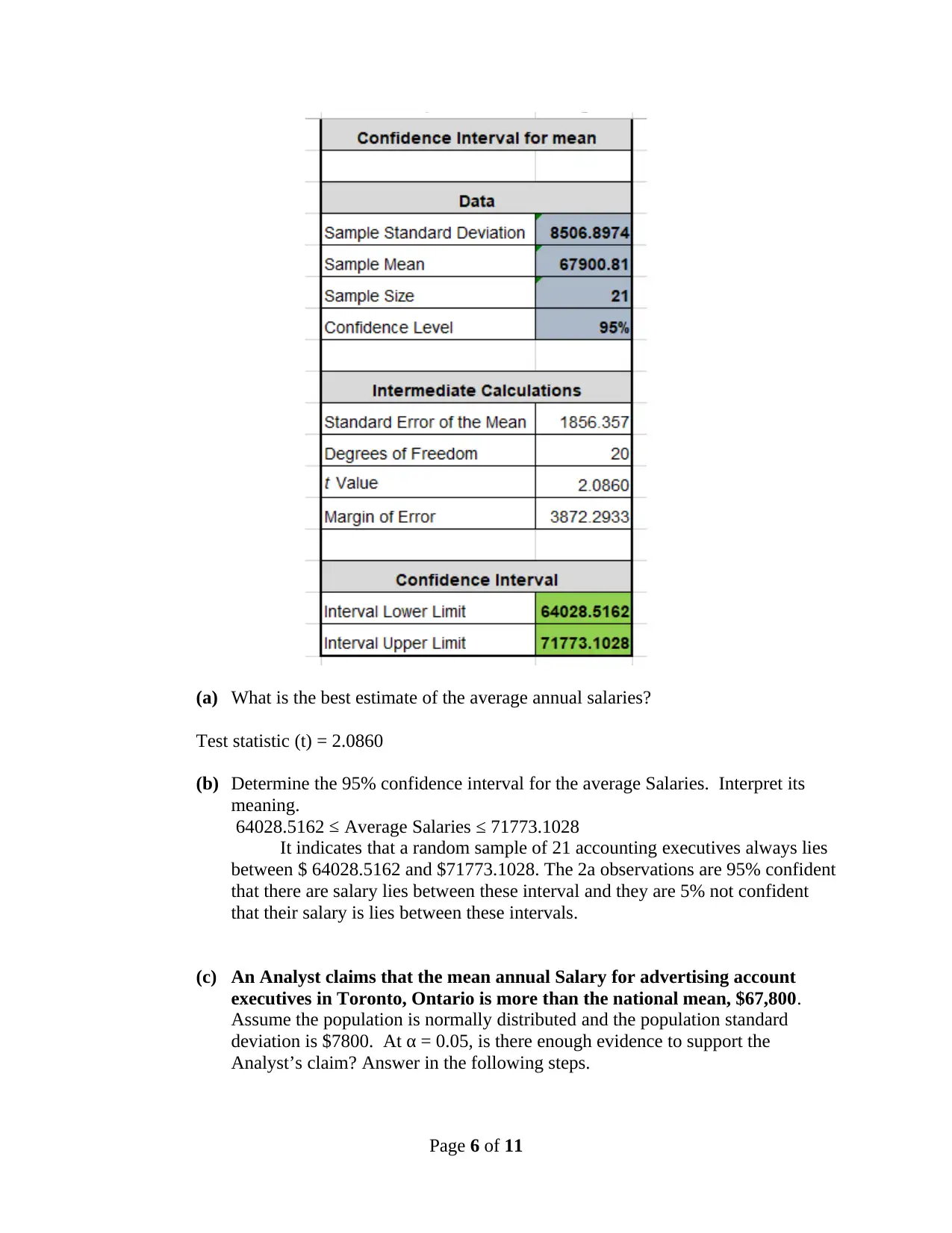
(a) What is the best estimate of the average annual salaries?
Test statistic (t) = 2.0860
(b) Determine the 95% confidence interval for the average Salaries. Interpret its
meaning.
64028.5162 ≤ Average Salaries ≤ 71773.1028
It indicates that a random sample of 21 accounting executives always lies
between $ 64028.5162 and $71773.1028. The 2a observations are 95% confident
that there are salary lies between these interval and they are 5% not confident
that their salary is lies between these intervals.
(c) An Analyst claims that the mean annual Salary for advertising account
executives in Toronto, Ontario is more than the national mean, $67,800.
Assume the population is normally distributed and the population standard
deviation is $7800. At α = 0.05, is there enough evidence to support the
Analyst’s claim? Answer in the following steps.
Page 6 of 11
Test statistic (t) = 2.0860
(b) Determine the 95% confidence interval for the average Salaries. Interpret its
meaning.
64028.5162 ≤ Average Salaries ≤ 71773.1028
It indicates that a random sample of 21 accounting executives always lies
between $ 64028.5162 and $71773.1028. The 2a observations are 95% confident
that there are salary lies between these interval and they are 5% not confident
that their salary is lies between these intervals.
(c) An Analyst claims that the mean annual Salary for advertising account
executives in Toronto, Ontario is more than the national mean, $67,800.
Assume the population is normally distributed and the population standard
deviation is $7800. At α = 0.05, is there enough evidence to support the
Analyst’s claim? Answer in the following steps.
Page 6 of 11

Step – (1) Null hypothesis: The mean annual Salary for advertising account
executives in Toronto is not more than 67800.
Step – (2) Alternative hypothesis: The mean annual Salary for advertising
account executives in Toronto is more than 67800.
Step – (3) Test statistic (t) = 0.0592
Step- (4) P-value= 0.4767
Step-(5) Alpha= 0.05
Step – (6) Conclusion: It is clear that P-value > alpha. Hence the null hypothesis
is not significant. Thus it may be summarized that the mean annual Salary for
advertising account executives in Toronto is not more than 67800.
Page 7 of 11
executives in Toronto is not more than 67800.
Step – (2) Alternative hypothesis: The mean annual Salary for advertising
account executives in Toronto is more than 67800.
Step – (3) Test statistic (t) = 0.0592
Step- (4) P-value= 0.4767
Step-(5) Alpha= 0.05
Step – (6) Conclusion: It is clear that P-value > alpha. Hence the null hypothesis
is not significant. Thus it may be summarized that the mean annual Salary for
advertising account executives in Toronto is not more than 67800.
Page 7 of 11
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

(d) Which type of error (I or II) might have occurred in your decision above?
Explain the error in that situation.
It is a type II error. Because in this problem accept the null hypothesis but it is
false. It has been seen that the average salary is 67900.81. But according to this
hypothesis test it calculated that the mean annual Salary for advertising account
executives in Toronto is not more than 67800. Hence it is a type two error.
4) Correlation (6 marks)
A study was conducted to analyze whether there is a linear relation between the number of
customers who visited a store and the total sales at that store.
The following data was collected over a period of 14 days:
Number of customers Total Sales(K)
125 35.1
88 28.5
111 30.3
121 36.2
102 33.4
98 30.2
106 31.2
133 44.5
128 39.4
105 32.5
118 33.2
127 40.5
144 58.2
136 41.3
(a) What is the dependent and independent variable?
The dependent variable is total sales and the independent variable is number of
customers.
(b) Prepare a scatter plot. What is the direction of correlation?
Page 8 of 11
Explain the error in that situation.
It is a type II error. Because in this problem accept the null hypothesis but it is
false. It has been seen that the average salary is 67900.81. But according to this
hypothesis test it calculated that the mean annual Salary for advertising account
executives in Toronto is not more than 67800. Hence it is a type two error.
4) Correlation (6 marks)
A study was conducted to analyze whether there is a linear relation between the number of
customers who visited a store and the total sales at that store.
The following data was collected over a period of 14 days:
Number of customers Total Sales(K)
125 35.1
88 28.5
111 30.3
121 36.2
102 33.4
98 30.2
106 31.2
133 44.5
128 39.4
105 32.5
118 33.2
127 40.5
144 58.2
136 41.3
(a) What is the dependent and independent variable?
The dependent variable is total sales and the independent variable is number of
customers.
(b) Prepare a scatter plot. What is the direction of correlation?
Page 8 of 11
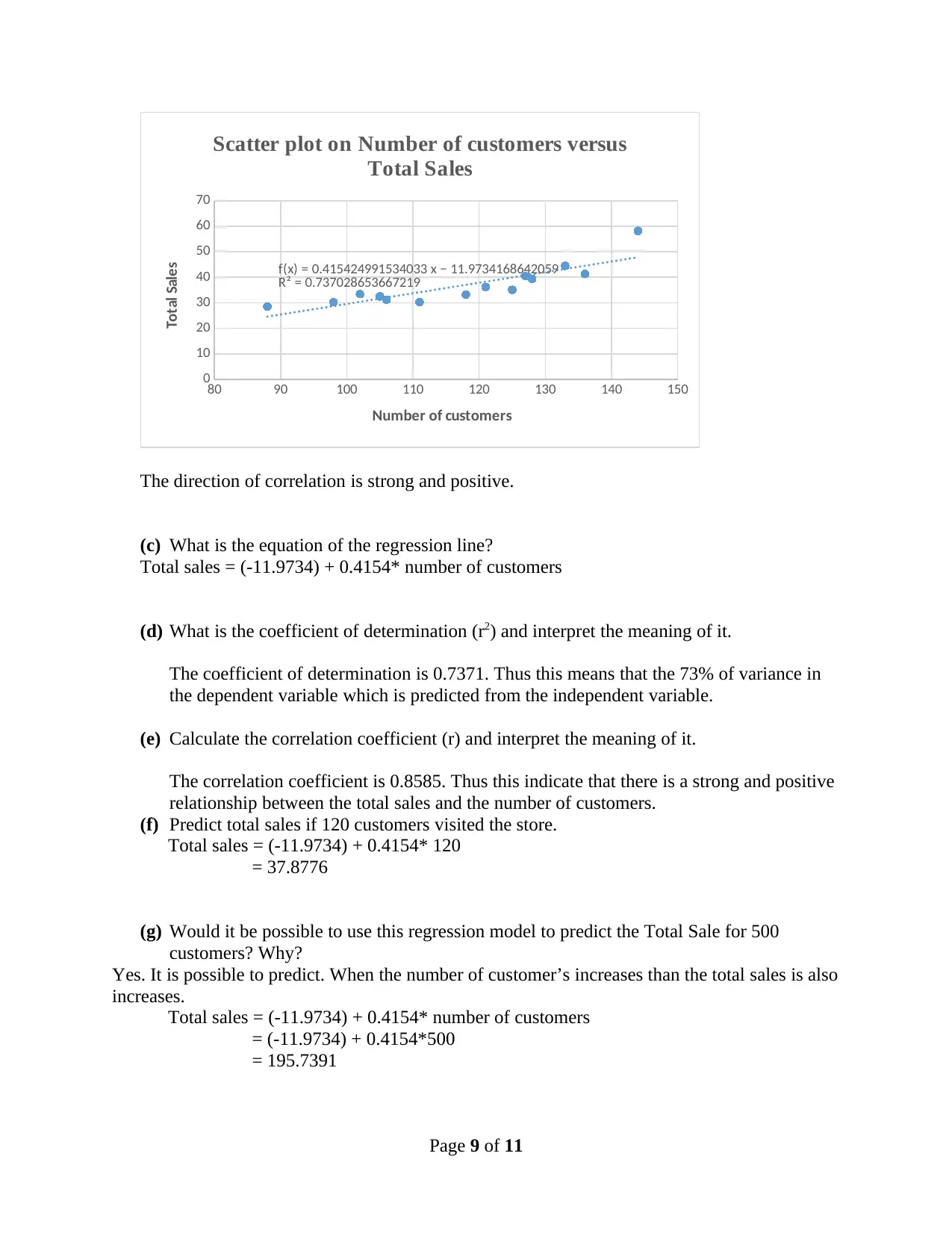
80 90 100 110 120 130 140 150
0
10
20
30
40
50
60
70
f(x) = 0.415424991534033 x − 11.9734168642059
R² = 0.737028653667219
Scatter plot on Number of customers versus
Total Sales
Number of customers
Total Sales
The direction of correlation is strong and positive.
(c) What is the equation of the regression line?
Total sales = (-11.9734) + 0.4154* number of customers
(d) What is the coefficient of determination (r2) and interpret the meaning of it.
The coefficient of determination is 0.7371. Thus this means that the 73% of variance in
the dependent variable which is predicted from the independent variable.
(e) Calculate the correlation coefficient (r) and interpret the meaning of it.
The correlation coefficient is 0.8585. Thus this indicate that there is a strong and positive
relationship between the total sales and the number of customers.
(f) Predict total sales if 120 customers visited the store.
Total sales = (-11.9734) + 0.4154* 120
= 37.8776
(g) Would it be possible to use this regression model to predict the Total Sale for 500
customers? Why?
Yes. It is possible to predict. When the number of customer’s increases than the total sales is also
increases.
Total sales = (-11.9734) + 0.4154* number of customers
= (-11.9734) + 0.4154*500
= 195.7391
Page 9 of 11
0
10
20
30
40
50
60
70
f(x) = 0.415424991534033 x − 11.9734168642059
R² = 0.737028653667219
Scatter plot on Number of customers versus
Total Sales
Number of customers
Total Sales
The direction of correlation is strong and positive.
(c) What is the equation of the regression line?
Total sales = (-11.9734) + 0.4154* number of customers
(d) What is the coefficient of determination (r2) and interpret the meaning of it.
The coefficient of determination is 0.7371. Thus this means that the 73% of variance in
the dependent variable which is predicted from the independent variable.
(e) Calculate the correlation coefficient (r) and interpret the meaning of it.
The correlation coefficient is 0.8585. Thus this indicate that there is a strong and positive
relationship between the total sales and the number of customers.
(f) Predict total sales if 120 customers visited the store.
Total sales = (-11.9734) + 0.4154* 120
= 37.8776
(g) Would it be possible to use this regression model to predict the Total Sale for 500
customers? Why?
Yes. It is possible to predict. When the number of customer’s increases than the total sales is also
increases.
Total sales = (-11.9734) + 0.4154* number of customers
= (-11.9734) + 0.4154*500
= 195.7391
Page 9 of 11
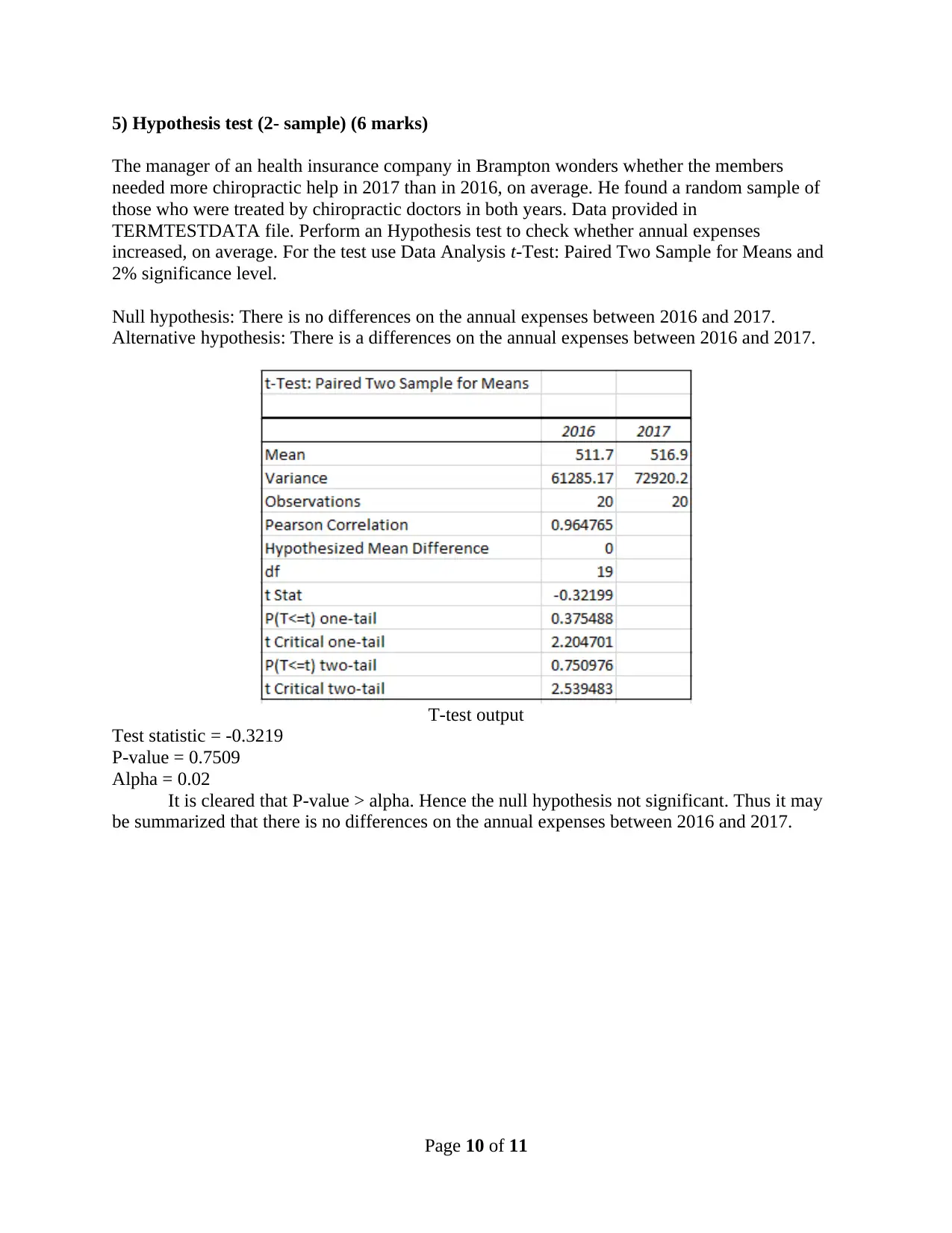
5) Hypothesis test (2- sample) (6 marks)
The manager of an health insurance company in Brampton wonders whether the members
needed more chiropractic help in 2017 than in 2016, on average. He found a random sample of
those who were treated by chiropractic doctors in both years. Data provided in
TERMTESTDATA file. Perform an Hypothesis test to check whether annual expenses
increased, on average. For the test use Data Analysis t-Test: Paired Two Sample for Means and
2% significance level.
Null hypothesis: There is no differences on the annual expenses between 2016 and 2017.
Alternative hypothesis: There is a differences on the annual expenses between 2016 and 2017.
T-test output
Test statistic = -0.3219
P-value = 0.7509
Alpha = 0.02
It is cleared that P-value > alpha. Hence the null hypothesis not significant. Thus it may
be summarized that there is no differences on the annual expenses between 2016 and 2017.
Page 10 of 11
The manager of an health insurance company in Brampton wonders whether the members
needed more chiropractic help in 2017 than in 2016, on average. He found a random sample of
those who were treated by chiropractic doctors in both years. Data provided in
TERMTESTDATA file. Perform an Hypothesis test to check whether annual expenses
increased, on average. For the test use Data Analysis t-Test: Paired Two Sample for Means and
2% significance level.
Null hypothesis: There is no differences on the annual expenses between 2016 and 2017.
Alternative hypothesis: There is a differences on the annual expenses between 2016 and 2017.
T-test output
Test statistic = -0.3219
P-value = 0.7509
Alpha = 0.02
It is cleared that P-value > alpha. Hence the null hypothesis not significant. Thus it may
be summarized that there is no differences on the annual expenses between 2016 and 2017.
Page 10 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

Page 11 of 11
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.




