Statistical Modeling: Forecasting When Women Will Outrun Men
VerifiedAdded on 2023/06/11
|7
|1332
|306
Report
AI Summary
This report analyzes historical 400m race data for men and women to predict when women might outrun men. It includes side-by-side box plots comparing winning times, highlighting differences in variability and skewness. Linear regression models are created from scatterplots of the data, and equations are used to algebraically determine the crossover point when women's times will be faster. The analysis considers university data and Olympic data, discussing the validity of extrapolating from these models and the limitations of assuming trends will continue. The report references statistical methods and data sources, with the conclusion pointing towards a future where women's race times could surpass men's, while acknowledging the potential for error in long-term predictions. Desklib provides this solved assignment along with a range of study resources including past papers to support students.

1
Will Women Ever Outrun Men?
Name of the author
State and country
Date:
Will Women Ever Outrun Men?
Name of the author
State and country
Date:
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
The dates and winning times (measured in
seconds) for a university’s men’s and
women’s annual 400m race are listed
below.
TABLE 1
Year Men Women
1975 51.11 58.42
1976 50.95 58.17
1977 50.48 57.96
1978 50.43 57.4
1979 50.68 57.51
1980 50.62 56.66
1981 50.82 56.02
1982 50.03 56.22
1983 49.64 56.88
1984 49.8 56.21
1985 49.91 55.02
1986 48.82 54.9
1987 48.81 54.92
1988 48.46 54.22
1989 48.19 53.61
1990 48.15 53.38
1991 48.66 53.06
1992 47.84 53
1993 47.45 52.23
1994 47.33 52.11
1995 47.55 51.51
1996 47.47 51.44
1997 46.93 51.02
1998 46.72 50.87
1999 45.99 50.77
2000 45.77 50.8
2001 45.98 49.64
2002 45.83 49.61
2003 45.81 48.73
2004 45.44 48.71
2005 45.03 48.13
Part A:
1. Construct side-by-side box plots to
compare Men’s and Women’s
winning times in the 400m race.
Make sure you include a scale.
Comment on any similarities and/or
differences between the plots.
Include your 5-number summary.
(5 marks U&F)
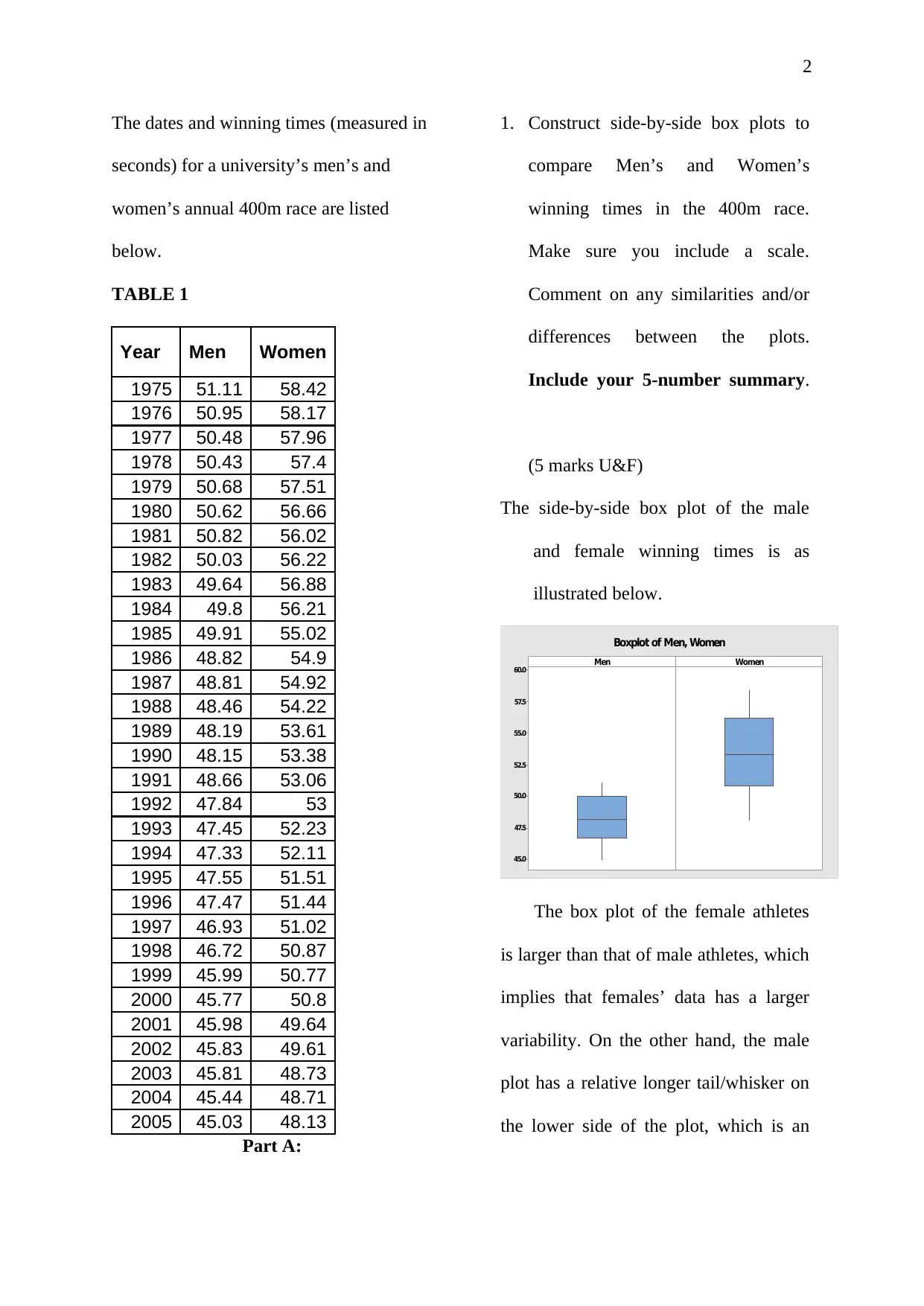
The side-by-side box plot of the male
and female winning times is as
illustrated below.
60.0
57.5
55.0
52.5
50.0
47.5
45.0
Men Women
Boxplot of Men, Women
The box plot of the female athletes
is larger than that of male athletes, which
implies that females’ data has a larger
variability. On the other hand, the male
plot has a relative longer tail/whisker on
the lower side of the plot, which is an
The dates and winning times (measured in
seconds) for a university’s men’s and
women’s annual 400m race are listed
below.
TABLE 1
Year Men Women
1975 51.11 58.42
1976 50.95 58.17
1977 50.48 57.96
1978 50.43 57.4
1979 50.68 57.51
1980 50.62 56.66
1981 50.82 56.02
1982 50.03 56.22
1983 49.64 56.88
1984 49.8 56.21
1985 49.91 55.02
1986 48.82 54.9
1987 48.81 54.92
1988 48.46 54.22
1989 48.19 53.61
1990 48.15 53.38
1991 48.66 53.06
1992 47.84 53
1993 47.45 52.23
1994 47.33 52.11
1995 47.55 51.51
1996 47.47 51.44
1997 46.93 51.02
1998 46.72 50.87
1999 45.99 50.77
2000 45.77 50.8
2001 45.98 49.64
2002 45.83 49.61
2003 45.81 48.73
2004 45.44 48.71
2005 45.03 48.13
Part A:
1. Construct side-by-side box plots to
compare Men’s and Women’s
winning times in the 400m race.
Make sure you include a scale.
Comment on any similarities and/or
differences between the plots.
Include your 5-number summary.
(5 marks U&F)
The side-by-side box plot of the male
and female winning times is as
illustrated below.
60.0
57.5
55.0
52.5
50.0
47.5
45.0
Men Women
Boxplot of Men, Women
The box plot of the female athletes
is larger than that of male athletes, which
implies that females’ data has a larger
variability. On the other hand, the male
plot has a relative longer tail/whisker on
the lower side of the plot, which is an

3
indication that their running time is
negatively skewed.
The five number summary is as
illustrated below.
Variable Minimum Q1 Median Q3 Maximum
Men 45.030 46.720 48.190 50.030 51.110
Women 48.130 50.870 53.380 56.220 58.420
The results show that the male has
the least finish time compared to females
with 48.281 seconds. Also, the median
run time for male is lower. The middle
fifty percent of the male run time is
between 46.720 seconds and 50.030
seconds whereas that of the female is
between 50.870 and 56.220. From this,
the IQR for male is 3.33 seconds and that
of female athletes is 5.35 [3]. This clearly
supports that the female athletes had a
higher variability in the winning time
than men.
2. Use your graphics calculator app to
plot scatterplots for each of the data
sets. Use the regression analysis tool
to produce two lines of best fit and
obtain an equation for each line.
(5 marks U&F)
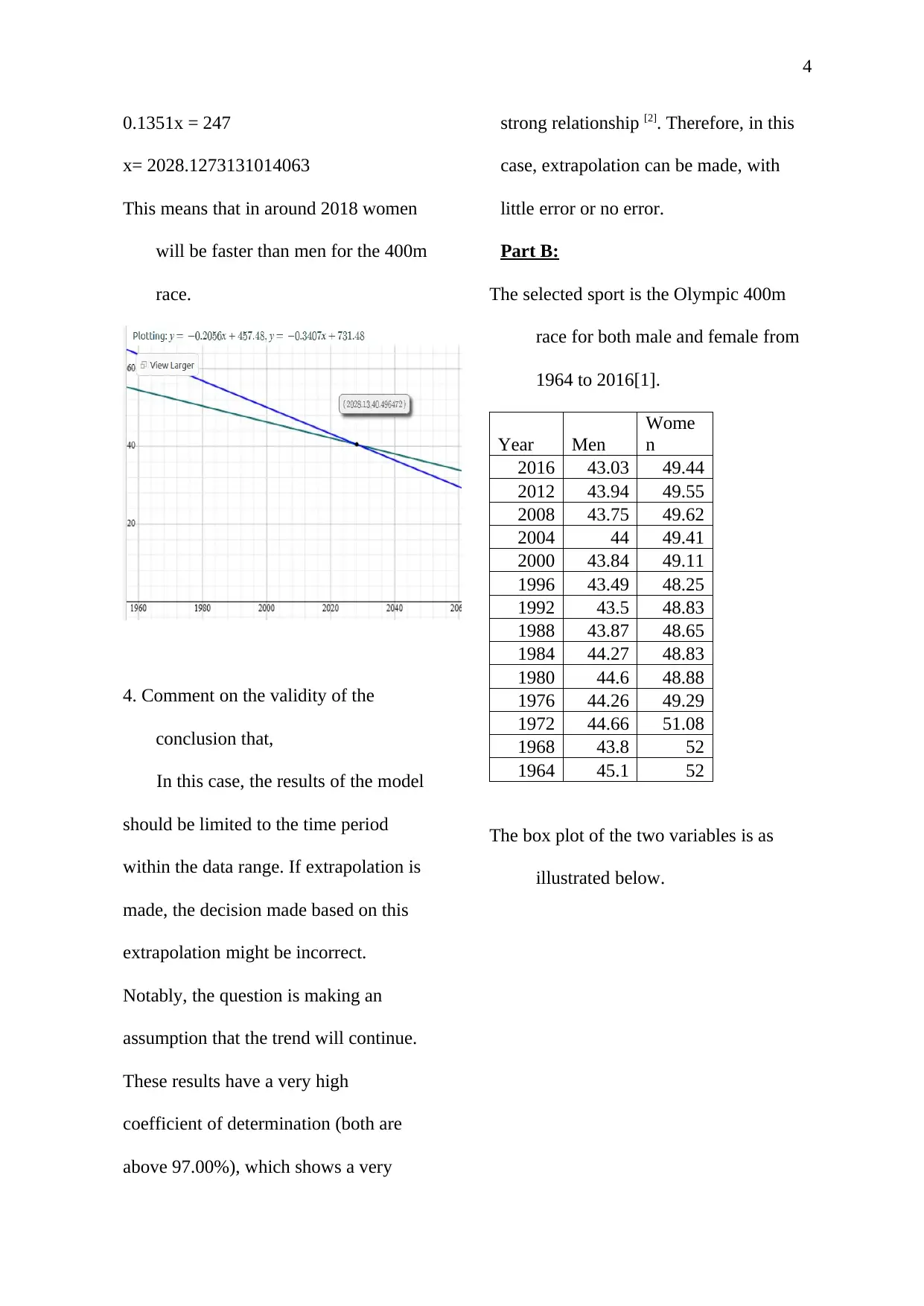
1975 1980 1985 1990 1995 2000 2005
40
50
60
f(x) = − 0.340681451612903 x + 731.476411290323
R² = 0.988839947256411f(x) = − 0.205629032258064 x + 457.482419354839
R² = 0.973320157877911
Winning Time for Male and
Female
Men Linear (Men)
Women Linear (Women)
Time
Winning Time (min)
The male linear model is: y = -0.2056x +
457.48, and the female winning time
model is: y = -0.3407x + 731.48
3. Use these two equations to find
algebraically when the university
women will be as fast as the
university men for the 400m race.
What will this time be? Explain your
working clearly.
Verify your result using the graphic
calculator app, include a screen shot.
(5 marks U&F)
The time when the female will run faster
than men is when the two algebraic
model are equal.
-0.2056x + 457.48 =-0.3407x + 731.48
indication that their running time is
negatively skewed.
The five number summary is as
illustrated below.
Variable Minimum Q1 Median Q3 Maximum
Men 45.030 46.720 48.190 50.030 51.110
Women 48.130 50.870 53.380 56.220 58.420
The results show that the male has
the least finish time compared to females
with 48.281 seconds. Also, the median
run time for male is lower. The middle
fifty percent of the male run time is
between 46.720 seconds and 50.030
seconds whereas that of the female is
between 50.870 and 56.220. From this,
the IQR for male is 3.33 seconds and that
of female athletes is 5.35 [3]. This clearly
supports that the female athletes had a
higher variability in the winning time
than men.
2. Use your graphics calculator app to
plot scatterplots for each of the data
sets. Use the regression analysis tool
to produce two lines of best fit and
obtain an equation for each line.
(5 marks U&F)
1975 1980 1985 1990 1995 2000 2005
40
50
60
f(x) = − 0.340681451612903 x + 731.476411290323
R² = 0.988839947256411f(x) = − 0.205629032258064 x + 457.482419354839
R² = 0.973320157877911
Winning Time for Male and
Female
Men Linear (Men)
Women Linear (Women)
Time
Winning Time (min)
The male linear model is: y = -0.2056x +
457.48, and the female winning time
model is: y = -0.3407x + 731.48
3. Use these two equations to find
algebraically when the university
women will be as fast as the
university men for the 400m race.
What will this time be? Explain your
working clearly.
Verify your result using the graphic
calculator app, include a screen shot.
(5 marks U&F)
The time when the female will run faster
than men is when the two algebraic
model are equal.
-0.2056x + 457.48 =-0.3407x + 731.48
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
4
0.1351x = 247
x= 2028.1273131014063
This means that in around 2018 women
will be faster than men for the 400m
race.
4. Comment on the validity of the
conclusion that,
In this case, the results of the model
should be limited to the time period
within the data range. If extrapolation is
made, the decision made based on this
extrapolation might be incorrect.
Notably, the question is making an
assumption that the trend will continue.
These results have a very high
coefficient of determination (both are
above 97.00%), which shows a very
strong relationship [2]. Therefore, in this
case, extrapolation can be made, with
little error or no error.
Part B:
The selected sport is the Olympic 400m
race for both male and female from
1964 to 2016[1].
Year Men
Wome
n
2016 43.03 49.44
2012 43.94 49.55
2008 43.75 49.62
2004 44 49.41
2000 43.84 49.11
1996 43.49 48.25
1992 43.5 48.83
1988 43.87 48.65
1984 44.27 48.83
1980 44.6 48.88
1976 44.26 49.29
1972 44.66 51.08
1968 43.8 52
1964 45.1 52
The box plot of the two variables is as
illustrated below.
0.1351x = 247
x= 2028.1273131014063
This means that in around 2018 women
will be faster than men for the 400m
race.
4. Comment on the validity of the
conclusion that,
In this case, the results of the model
should be limited to the time period
within the data range. If extrapolation is
made, the decision made based on this
extrapolation might be incorrect.
Notably, the question is making an
assumption that the trend will continue.
These results have a very high
coefficient of determination (both are
above 97.00%), which shows a very
strong relationship [2]. Therefore, in this
case, extrapolation can be made, with
little error or no error.
Part B:
The selected sport is the Olympic 400m
race for both male and female from
1964 to 2016[1].
Year Men
Wome
n
2016 43.03 49.44
2012 43.94 49.55
2008 43.75 49.62
2004 44 49.41
2000 43.84 49.11
1996 43.49 48.25
1992 43.5 48.83
1988 43.87 48.65
1984 44.27 48.83
1980 44.6 48.88
1976 44.26 49.29
1972 44.66 51.08
1968 43.8 52
1964 45.1 52
The box plot of the two variables is as
illustrated below.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

5
52
50
48
46
44
42
Men Women
Boxplot of Men, Women
The box plot deduces that the
females winning time is more disperse that
that of men. Also, there are two points that
are outliers in the female dataset. Both
have a slightly longer tail on the right of
the plot, which deduces that they have a
positive skewness. The five number
summary is as illustrated below.
Variable Minimum Q1 Median Q3 Maximum
Men 43.030 43.688 43.905 44.352 45.100
Women 48.250 48.830 49.350 49.985 52.000
The results indicate that the male
athletes the minimum finish time with
44.03 secs. The male also has a slightly
lower median. The IQR for the men
finishes time is 0.663 sec, whereas that of
the female is 1.155sec, which clearly
supports that female winning time is
higher than that of the male. The middle
50% of the data for male are between
43.688 secs, and 44.352 secs, whereas
that of female athletes is between 48.830
secs and 49.985 secs [2].
The scatter plot of the data is as
illustrated below.
1960 1970 1980 1990 2000 2010 2020
40
45
50
55
f(x) = − 0.0400769230769231 x
+ 129.391648351648
R² = 0.315688813912933f(x) = − 0.0230164835164835 x
+ 89.8106593406593
R² = 0.514928059902568
Olympic winning Time
400m
Men
Linear (Men)
Women
Linear (Women)
Year
Winning time
The two algebraic equations that
show the relationship between winning
time and time are:
Men: y = -0.023x + 89.811
Women: y = -0.0401x + 129.39
The women will overrun the men in
400m when their speed is equal
-0.023x + 89.811 = -0.0401x +
129.39
X = 2314.5614035087719
52
50
48
46
44
42
Men Women
Boxplot of Men, Women
The box plot deduces that the
females winning time is more disperse that
that of men. Also, there are two points that
are outliers in the female dataset. Both
have a slightly longer tail on the right of
the plot, which deduces that they have a
positive skewness. The five number
summary is as illustrated below.
Variable Minimum Q1 Median Q3 Maximum
Men 43.030 43.688 43.905 44.352 45.100
Women 48.250 48.830 49.350 49.985 52.000
The results indicate that the male
athletes the minimum finish time with
44.03 secs. The male also has a slightly
lower median. The IQR for the men
finishes time is 0.663 sec, whereas that of
the female is 1.155sec, which clearly
supports that female winning time is
higher than that of the male. The middle
50% of the data for male are between
43.688 secs, and 44.352 secs, whereas
that of female athletes is between 48.830
secs and 49.985 secs [2].
The scatter plot of the data is as
illustrated below.
1960 1970 1980 1990 2000 2010 2020
40
45
50
55
f(x) = − 0.0400769230769231 x
+ 129.391648351648
R² = 0.315688813912933f(x) = − 0.0230164835164835 x
+ 89.8106593406593
R² = 0.514928059902568
Olympic winning Time
400m
Men
Linear (Men)
Women
Linear (Women)
Year
Winning time
The two algebraic equations that
show the relationship between winning
time and time are:
Men: y = -0.023x + 89.811
Women: y = -0.0401x + 129.39
The women will overrun the men in
400m when their speed is equal
-0.023x + 89.811 = -0.0401x +
129.39
X = 2314.5614035087719

6
This means that in the year around
2314, the female athletes will be faster
than men.
This supports the conclusion made
earlier that in the year 2314 women will
be faster than men.
These results have limitation as
there was weak association between both
male and female winning time. Thus,
making the decision for years above 2016
will result in an error. The results can only
be used to shows that the female winning
time is reducing more than that of male
athletes. That is, the gradients can be
compared to show which one is reducing
on average more than the other.
This means that in the year around
2314, the female athletes will be faster
than men.
This supports the conclusion made
earlier that in the year 2314 women will
be faster than men.
These results have limitation as
there was weak association between both
male and female winning time. Thus,
making the decision for years above 2016
will result in an error. The results can only
be used to shows that the female winning
time is reducing more than that of male
athletes. That is, the gradients can be
compared to show which one is reducing
on average more than the other.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
References
[1] "400m women - Olympic Athletics",
International Olympic Committee, 2018.
[Online]. Available:
https://www.olympic.org/athletics/400m-
women. [Accessed: 04- Jun- 2018].
[2] P. Newbold, W. Carlson and B.
Thorne, Statistics for business and
economics. Harlow, Essex: Pearson
Education, 2013.
[3] G. Keller, Statistics for management
and economics, 10th ed. Stamford:
Cengage Learning, 2014, p. 994.
References
[1] "400m women - Olympic Athletics",
International Olympic Committee, 2018.
[Online]. Available:
https://www.olympic.org/athletics/400m-
women. [Accessed: 04- Jun- 2018].
[2] P. Newbold, W. Carlson and B.
Thorne, Statistics for business and
economics. Harlow, Essex: Pearson
Education, 2013.
[3] G. Keller, Statistics for management
and economics, 10th ed. Stamford:
Cengage Learning, 2014, p. 994.
1 out of 7
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
