University Assignment: ACC4018 Linear Programming Problem Solution

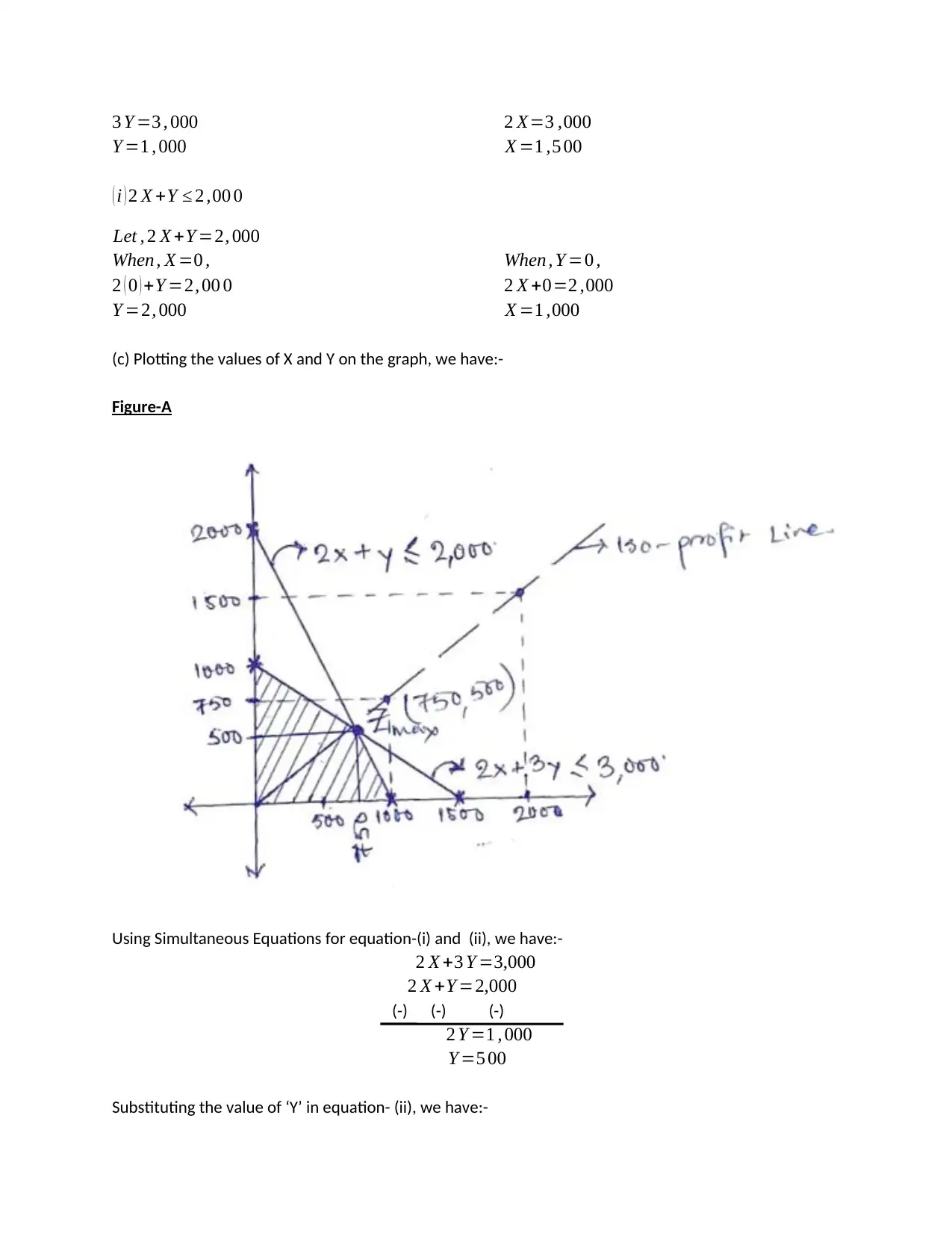
This document presents a comprehensive solution to a linear programming problem, specifically addressing the ACC4018 Quantitative Methods for Accountants assignment. The problem involves a turbo engine manufacturer producing two models, Fusion and Torque, with constraints on labor and capital hours. The solution begins by formulating the problem mathematically, defining the objective function (maximizing profit) and constraints. It then proceeds to solve the problem using graphical methods, plotting the feasible region and identifying the optimal production levels of Fusion and Torque to maximize profit. The solution also includes an analysis of the iso-profit line to determine the optimal solution. The document provides detailed workings, graphical representations, and references to support the solution. The assignment demonstrates the application of linear programming in a business context, showcasing how to optimize production and maximize profits under given constraints.

Linear Programming Problem
‘The mathematical experience of the student is incomplete if he never had the opportunity to solve a
problem invented by himself (Polya, 2014) ‘. In today’s world, we come across many such situations
wherein we try to assess which combinations of two particular things are taken from varied options or in
what proportion should two things be taken so that the cost is minimum (or the profit is maximized).
This type of inequalities (or variations) form a general class of problems called optimization problems
which aim to maximize profit or minimize cost under a given set of constraints or restrictions.
Linear Programming Problem is an important class of optimization problem. Let us explain this with the
help of an example. Suppose, a man has £1,20,000 to invest. He has option to buy a bag worth £600 and
shoes worth £1,000. He understands that by selling one bag, he can earn a profit of £80 and £120 by
selling one shoe. He owns a storage space that can store up to 150 pieces. He now wants to know what
quantity of the items he should buy so as to maximize the profit, assuming that he sells all the stuff that
he buys.
In the situation mentioned above, the man can buy 200 bags (£1,20,000 divided by £600) that can fetch
him a profit of £16,000 or he can buy 120 shoes that can fetch him a profit of £14,400. But in the first
option, he cannot buy 200 pieces as his storage space is limited to 150 while in the second option he can
buy all 120 shoes but the profit that he will receive is less than his first option. In this case the Linear
Programming problem method tries to mathematically formulate the problem subject to the constraints
determined by a set of linear inequalities with non-negative variables and finds out the optimal value
from a set of values that maximizes the profit of the person.
Linear Programming Problem has some terms that are defined as follows:-
Objective Function- It is linear function, i.e. Z = ax + by which needs to be maximized or minimized as
per the case.
Constraints- These are linear inequalities or restrictions within which the problem needs to be solved
and are non-negative.
Linear Programming problem finds its huge application in the different areas such as, management
science, commerce and industry.
Let us now solve the problem given in the assignment as per the Linear Programming Problem model
discussed above.

Solution:-
Let ‘X’ be the number of units of Fusion produced per day and ‘Y’ be the number of units of Torque
produced per day.
(a) Therefore, as per the information provided, the data can be tabulated as follows:-
Model Sales (£) Cost (£) Profit (£) Labor (in hours) Capital (in hours)
Fusion 16000 10000 6000 40 40
Torque 20000 12000 8000 60 20
Constraints given:-
Total Labor Hours available per day- 60,000 hours.
Total Capital Hours available per day- 40,000 hours.
(b) We now have the following mathematical model for the given problem, where the objective function
is as follows:-
Max Z=£ 6000 X+£ 8000 Y ,
Subject to the constraints:-
( i ) 40 X +60 Y ≤6 0 , 000
¿ , 2 X +3 Y ≤ 3 , 000
( ii ) 40 X +20 Y ≤ 4 0,000
¿ , 2 X +2Y ≤ 2 ,000
( ii i ) X , Y ≥ 0
Constraint Workings:-
( i ) 2 X +3 Y ≤ 3 ,00 0
Let , 2 X +3 Y =3 , 000
When , X =0 , When , Y =0 ,
2 ( 0 ) +3 Y =3 , 00 0 2 X +3 ( 0 ) =3 ,000

3 Y =3 , 000 2 X=3 ,000
Y =1 , 000 X =1 ,5 00
( i ) 2 X +Y ≤ 2 ,00 0
Let , 2 X +Y =2, 000
When , X =0 , When , Y =0 ,
2 ( 0 ) +Y =2, 00 0 2 X +0=2 ,000
Y =2, 000 X =1 ,000
(c) Plotting the values of X and Y on the graph, we have:-
Figure-A
Using Simultaneous Equations for equation-(i) and (ii), we have:-
2 X +3 Y =3,000
2 X +Y =2,000
(-) (-) (-)
2 Y =1 , 000
Y =5 00
Substituting the value of ‘Y’ in equation- (ii), we have:-

2 X +Y =2, 000
2 X +500=2, 000
2 X=2 , 000−500
2 X=1 , 5 00
X =1500
2 =750
Thus, the shaded region provides the feasible region where the profit can be maximized with the point
Zmax showing the maximum profitability combination of units to be produced for Fusion and Torque,
which have been derived by the simultaneous equation.
Therefore,
Number of Fusion to be produced per day= 750 units.
Number of Fusion to be produced per day= 500 units.
AND,
The maximum profit that can be achieved is,
£ 6000 ( 750 ) + £ 8000 ( 500 )
¿ £ 45,00,000+ £ 40,00 , 000
¿ £ 8 5,00,000 .
(d) Iso-profit Line
Consider the objective function,
Z=£ 6000 X + £ 8000 Y
Taking the L.C.M. of the co-efficient of X and Y and dividing it by 2, we have:-
Z=24,000
2 =12,000
Therefore,
£ 12,000=£ 6000 X +£ 8000 Y
When , X =0 , When , Y =0 ,
8,000 Y =12 , 00 0 6,000 X =12, 000
Y = 12 , 000
8,000 X =12,000
6 ,000
Y =1 .5 X =2
Now, X-value must increase by 2 and Y-value must increase by 1.5.
Therefore, the co-ordinates of X and Y for the Iso-profit function is as follows:-
X 1,000 2,000
Y 750 1,500
Plotting the co-ordinates of the Iso-profit function on the graph (Figure-A above), we see that the Iso-
profit line passes through the Zmax point (or maximum profitability point) at (700, 500).
Hence, the point (750, 500) is the optimal solution of maximizing the Z-value.

References
Polya, G. (2014). How to Solve It. Princeton University Press.
Walters, H. and Hartley, R. (1985). Linear and Non-Linear Programming: An Introduction to
Linear Methods in Mathematical Programming. The Journal of the Operational Research Society, 36(11),
p.1071.
Ncert.nic.in. (2019). [online] Available at: http://ncert.nic.in/ncerts/l/lemh206.pdf [Accessed 4 Oct.
2019].
Simonnard, M. (1966). Linear programming. Englewood Cliffs, N.J.: Prentice-Hall.
Curwin, J., Slater, R. and Eadson, D. (2013). Quantitative methods for business decisions. 5th
ed. Hampshire: Cengage Learning.