ACTST861 - Risk Theory: Assignment 1 - Weibull, Pareto, Lognormal

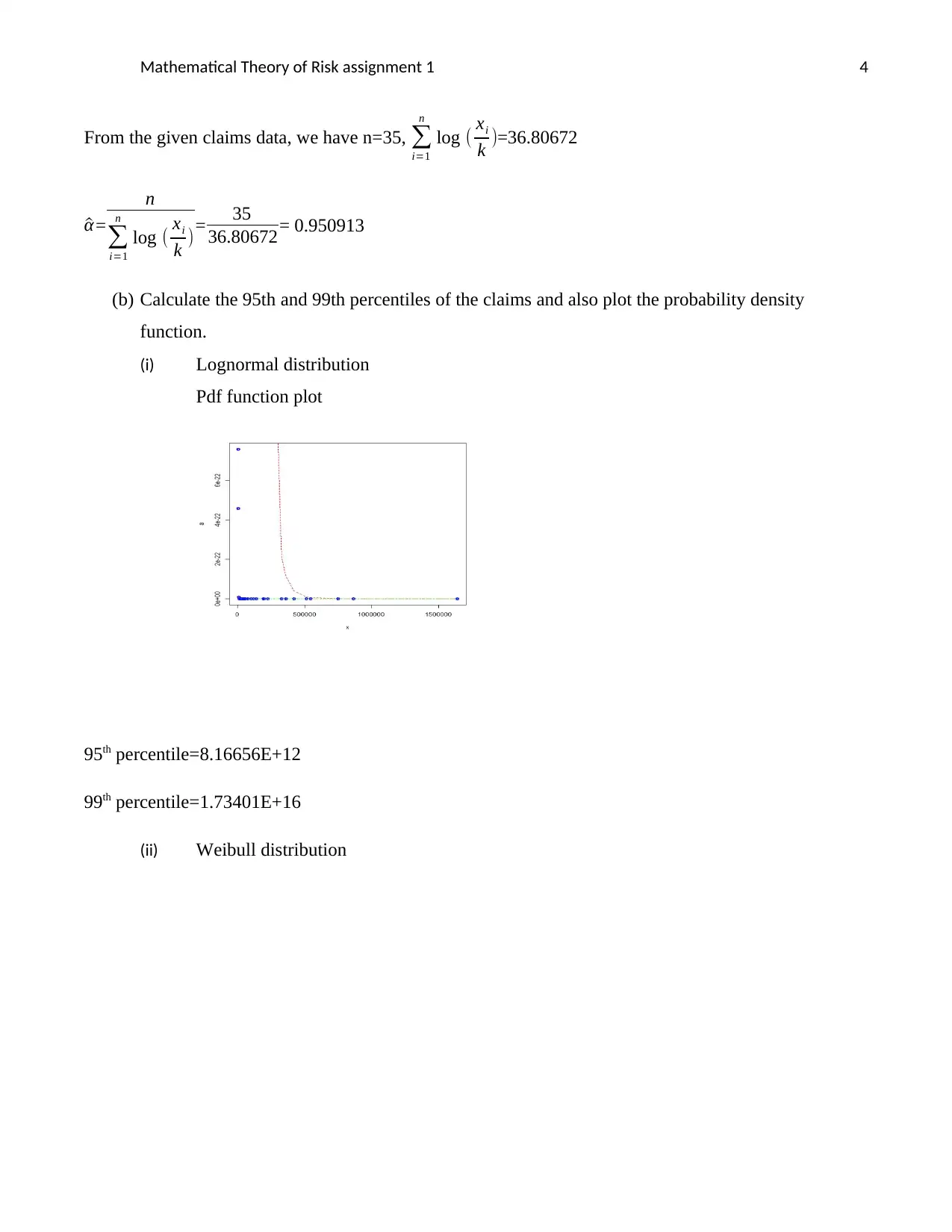
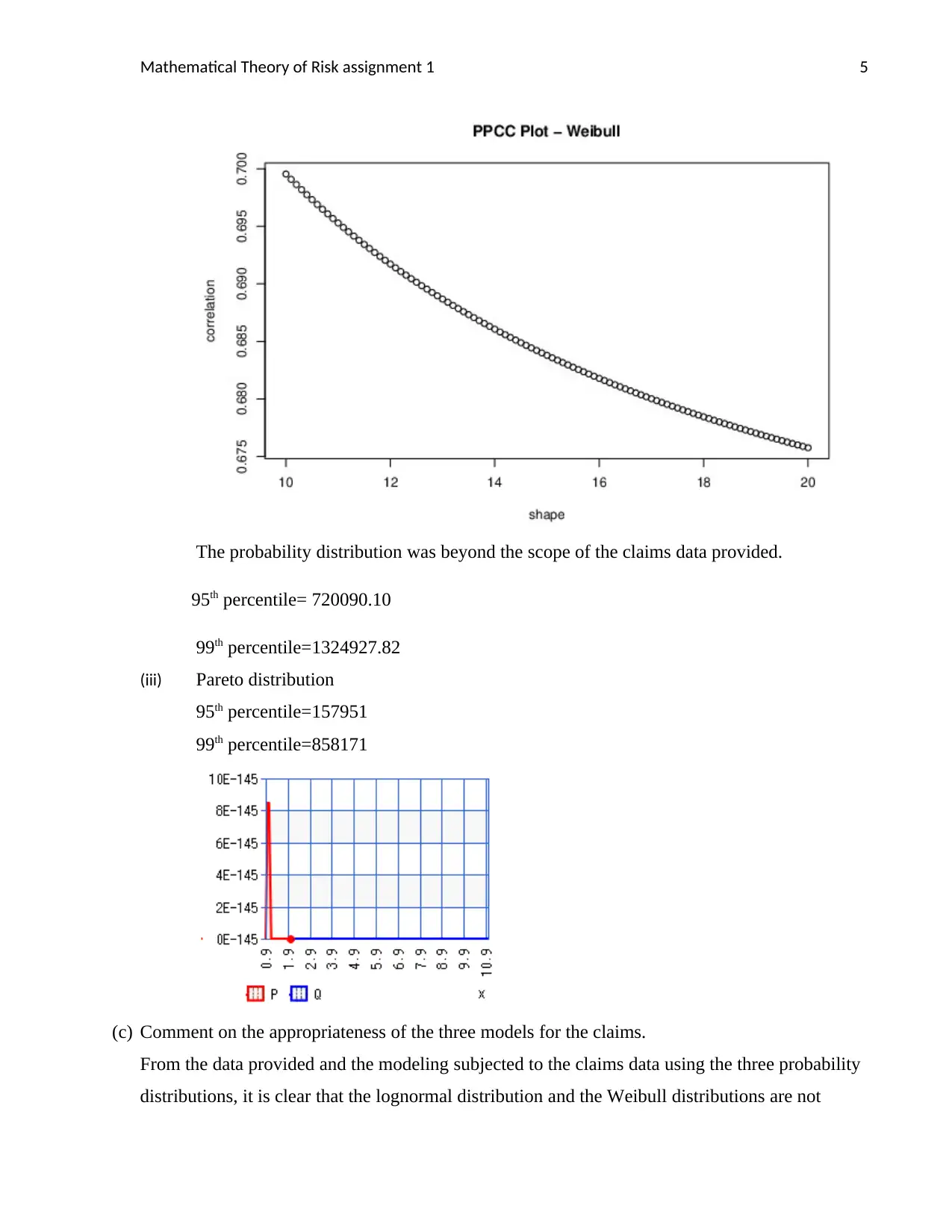
This assignment solution focuses on the mathematical theory of risk, specifically addressing parameter estimation for the Weibull, Pareto, and Lognormal distributions using the maximum likelihood method. The solution involves estimating parameters for each distribution using a given claims dataset, calculating the 95th and 99th percentiles of the claims, plotting the probability density functions, and commenting on the appropriateness of each model for the claims data. The analysis concludes that the Pareto distribution is the most appropriate model due to the outlier parameters produced by the data for lognormal and Weibull distributions, making it hard for the two probability distributions to fit the data. Desklib offers a range of study tools and resources, including solved assignments and past papers, to support students in their academic endeavors.

Mathematical Theory of Risk assignment 1 1
Mathematical Theory of Risk
Assignment 1
Student Name
Course Code: ACTST861
Associate Professor Jackie Li

Mathematical Theory of Risk assignment 1 2
(a) Using the maximum likelihood method to estimate the model parameters for Weibull, Pareto and
Lognormal distribution.
(i) Weibull distribution Maximum Likelihood estimate.
The weibull probability density function
f ( x ) = Υ
α ¿) x ≥ 0 , Υ >0 , α >0
The probability density function above is chosen for purposes of simplifying the
maximum likelihood function
L ( x1 , … , xn ;Υ , α ) =∏
i=1
n
¿ ¿
We take the logarithm of L ( x1 , … , xn ;Υ , α ) and differentiating with respect to Υ ∧α in
turns and equating it to zero to obtain the estimators of the equation.
∂ ln L
∂Υ = n
Υ +∑
i=1
n
ln xi− 1
α ∑
i=1
n
xi
Υ ln xi=0
∂ ln L
∂Υ =−n
α + 1
α2 ∑
i=1
n
xi
Υ
We eliminate α from the equation
∑
i=1
n
xi
Υ ln xi
∑
i=1
n
xi
Υ
− 1
Υ = 1
n ∑
i=1
n
ln xi
The estimate of parameter Υ is thus
^Υ = 1
n ∑
i=1
n
ln xi
The α estimator is thus
^α = 1
n ∑
i =1
n
xi
^Υ
From the given data we can estimate the parameters using excel
^Υ = 1
n ∑
i=1
n
ln xi= 393.4389
35 =0.705207301
^α = 1
n ∑
i =1
n
xi
^Υ = 151947.9155

Mathematical Theory of Risk assignment 1 3
(ii) Log normal distribution MLE
The parameter estimates for the maximum likelihood.
L ( μ , σ 2 ׀ X ) =∏
i=1
n
[f (xi∨¿ μ , σ2)]¿
Deriving the parameter from the above we will have
^μ=
∑
i=1
n
ln xi
n
From the given data, using excel we find the values of ∑
i=1
n
ln xi=393.4389
The value of n=35
^μ=
∑
i=1
n
ln xi
n
= 393.4389
35
^μ=11.24111
The Maximum Likelihood estimate of σ 2 for a lognormal distribution is:
^σ 2=∑
i=1
n
¿¿ ¿
^σ 2= 4422.049
35 =126.3442
(iii) The pareto distribution MLE for parameters given the data
f ( x|α , k )= α kα
xα+1 k ≤ x ≤ ∞ , α , k >0
The MLE of α is ^α =
n
∑
i=1
n
log ( xi
k )
The MLE of k=min{ xi } Thus k=6766

Mathematical Theory of Risk assignment 1 4
From the given claims data, we have n=35, ∑
i=1
n
log ( xi
k )=36.80672
^α=
n
∑
i=1
n
log ( xi
k )= 35
36.80672= 0.950913
(b) Calculate the 95th and 99th percentiles of the claims and also plot the probability density
function.
(i) Lognormal distribution
Pdf function plot
95th percentile=8.16656E+12
99th percentile=1.73401E+16
(ii) Weibull distribution

Mathematical Theory of Risk assignment 1 5
The probability distribution was beyond the scope of the claims data provided.
95th percentile= 720090.10
99th percentile=1324927.82
(iii) Pareto distribution
95th percentile=157951
99th percentile=858171
(c) Comment on the appropriateness of the three models for the claims.
From the data provided and the modeling subjected to the claims data using the three probability
distributions, it is clear that the lognormal distribution and the Weibull distributions are not

Mathematical Theory of Risk assignment 1 6
appropriate in the modeling of the data. The parameters produced by the data are outliers and this
makes it hard for the two probability distributions to fit the data. The pareto distribution indicates
a precision as far as the estimation of the percentiles are concerned and thus the most appropriate
in the modeling of the claims data. From the data obtained and the estimates calculated, we can
use the pareto distribution for modeling the claims.