The University of Adelaide - URM Walls Shear Response Analysis

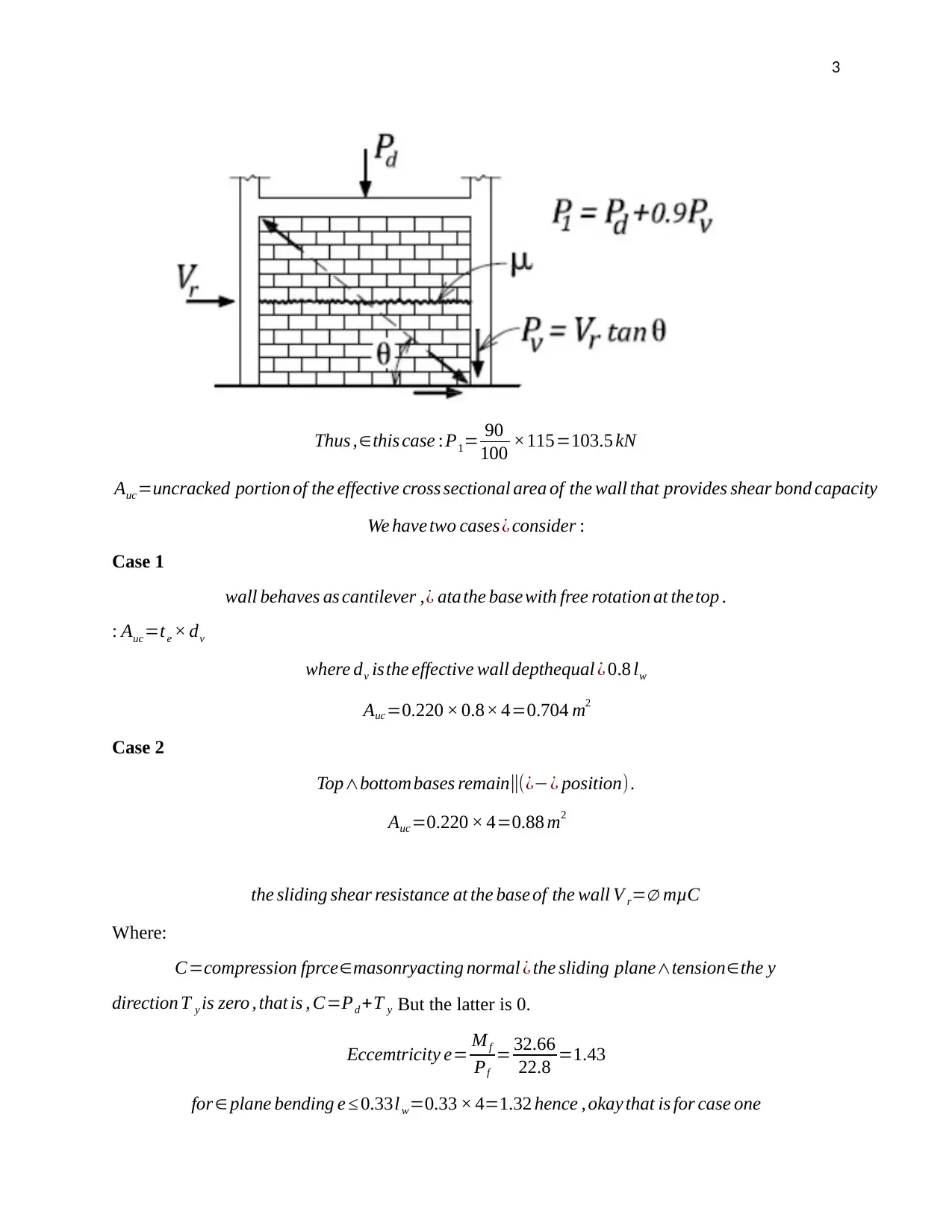
This document presents a solved homework assignment from the University of Adelaide's Seismic Design of Masonry Buildings course, focusing on the shear response of unreinforced masonry (URM) walls. The assignment involves analyzing a URM wall with given dimensions and material properties to determine its adequacy under seismic loading conditions. The solution includes calculations for flexural tensile stress, in-plane sliding shear resistance, and compression capacity, ensuring that the maximum stress does not exceed allowable limits. Various parameters such as wall length, height, thickness, and material strengths are considered in the analysis. The document also includes formulas and checks related to eccentricity, flexural strength, and shear capacity based on ASTM standards. Desklib provides a platform for students to access similar solved assignments and study resources.

1
The University of Adelaide
Department of Civil, Environmental and, Mining engineering
Seismic Design of Masonry Buildings
Semester 2, 2018
Instructor: M.C. Griffith
Homework Assignment #3
“Shear response of URM walls”.
Date: 08-Sep-18
Given the following as in the question outline
Wall length l=4m, height h=2.5m, thickness t=220mm
Length of walletes l= 0.77m, h=0.66m. t=0.220m and a mean failure load of 1016KN
Diagonal compression tests on square panels size l=077m, h=0.77m, t=0.220m and a mean
failure load of115 kN
Unit weight of brick masonry as 19Kn/m3
SOLUTION
f tu
, = 0.5 Pu
¿
f tu
, =0.5 × 115
0.77 ×0.220 =339.43 kN
m2
assuming a seismic designcategory A ; Load combinationA [ 0.6 D+ wL ] will govern
wL=19 × 4 ×2.5 × 0.220=41.8 kN
¿ 0.6 × 4.0+41.8=44.2kN
Maximum moment at h
2 , that is , mid−height of the masonry wall is as follow ;
M max = wL h2
8 → 41.8 × 2.52
8 =32.66 kNm

2
the axial force on the masonry P ;
p=0.6 ×wwall × h
2 =0.6 ×19 × 4
2 =22.8 kN
m2
theflexural tensile stressis calculated as below ;
−P
An
+ 12 M
Sn
,
where , An=te . lw effective cross−sectional areaof masonry
Sn= [ te × lw
2 ]
6
e <0.33 lw for∈− plane bending∨¿
e <0.33 t for ou of planebending ,
An =0.220 ×4=0.88 m2
Sn=0.220× 42
6 =0.587
therefore , flexural tensile stress is calculated by substitution∈the formula as shown;
−22.8
0.88 +12× 32.66
0.59 =−25.90+664.27
¿ 638.27 kN /m2
The allowable stress Ft , is 638 kN
m2 hence ,the masorny wallis adequate .
The∈− plane sliding shear resistance V r , along bed jointsbetween masonry courses
V r =0.16 ∅ m √ [ f m
, Auc ] +∅ mμ P1 where :
μ=coefficient of friction
¿ 0.7 for masonry smooth concrete
P1=compressive force ∈masonry acting normal ¿ the sliding plane
normallytaken as 0.9×the dead load .
V r =0.16 ×0.85 √ [ 300000× 0.88 ] +0.85 ×0.5 ×103.5
V r =113.87 kN

3
Thus ,∈this case :P1= 90
100 ×115=103.5 kN
Auc=uncracked portion of the effective cross sectional area of the wall that provides shear bond capacity
We have two cases¿ consider :
Case 1
wall behaves as cantilever ,¿ atathe base with free rotation at thetop .
: Auc=te × dv
where dv isthe effective wall depthequal ¿ 0.8 lw
Auc =0.220 × 0.8× 4=0.704 m2
Case 2
Top∧bottom bases remain∥(¿−¿ position).
Auc=0.220 × 4=0.88 m2
the sliding shear resistance at the base of the wall V r=∅ mμC
Where:
C=compression fprce∈masonryacting normal ¿ the sliding plane∧tension∈the y
direction T y is zero , that is , C=Pd +T y But the latter is 0.
Eccemtricity e= M f
Pf
= 32.66
22.8 =1.43
for ∈plane bending e ≤ 0.33l w=0.33 × 4=1.32 hence , okay that is for case one

4
for outof plane bending e ≤ 0.33 te=0.33× 0.220=0.726 , hence okay ∈case 2
ˇfor flexural strengthof masonry wall :
maximum stress musnot exceed ∅ m f m for tension∧¿
∅ m f t for compression
maximum stress at wall ends is at follows ;
Maximum f c= Pf
Ae
+ M f
Sn
= 22.8
0.88 + 32.66
0.59 ≤ ∅ m f m
, =0.85 ×300000 →{0.3M/mm2 into N/M2}
Maximum f c=81.27 ≤255000. therefore okay .
the compression capaciy of the masonry wall Pr = [ 0.85 ẓ ∅ m f m
, ] te ( lw
2 −e ).2
Pr =[0.85 ×0.5 × 0.66× 300000]0.220 ( 4
2 −1.43 ) .2
The Compression capacity of te masonry wall Pr =21.10 kN /m2
f sp= 2 P
π an
=2× 103.5
π ×0.77 × 0.66 =129.65 kN /m2
V ¿=V test
Ab
−PD +L(ASTM C 496)
V ¿= 1016
4 × 2.5 −22.8=78.8 kN
V m =0.56 V t + 0.75 PD
A ( Section A 106.3.3 .5 )
V m =0.56 ×115+0.75 × 10.88
4 ×0.220 =73.67 kN
V = 0.75 SDS W
R ( Equation A 1−7 )
V =0.75× 3.426 × 44.2
1.5 ( Valueof R as ∈table ASTM 496 )
V =75.72 kN

5