Advanced Computer Aided Engineering Project: Structural Analysis
VerifiedAdded on 2020/02/24
|9
|421
|109
Project
AI Summary
This project focuses on the numerical analysis of structural elements, specifically addressing stress, strain, and displacement calculations. It involves the application of finite element analysis principles to solve problems related to two-dimensional plane elasticity and the behavior of structural components under load. The solution outlines the steps to calculate the element stiffness matrix, strain/displacement matrix, and nodal displacements. It includes calculations for bending moments, reactions at supports, and stress/strain values. Furthermore, the project incorporates the analysis of axial forces and bending moments within a structural element, demonstrating how to compute key parameters such as inertia, nodal displacement, and stress. The project provides detailed solutions, including formulas, calculations, and final answers for various scenarios, making it a valuable resource for students studying mechanical engineering and related fields. The document is available on Desklib, a platform offering AI-based study tools for students.
1 out of 9





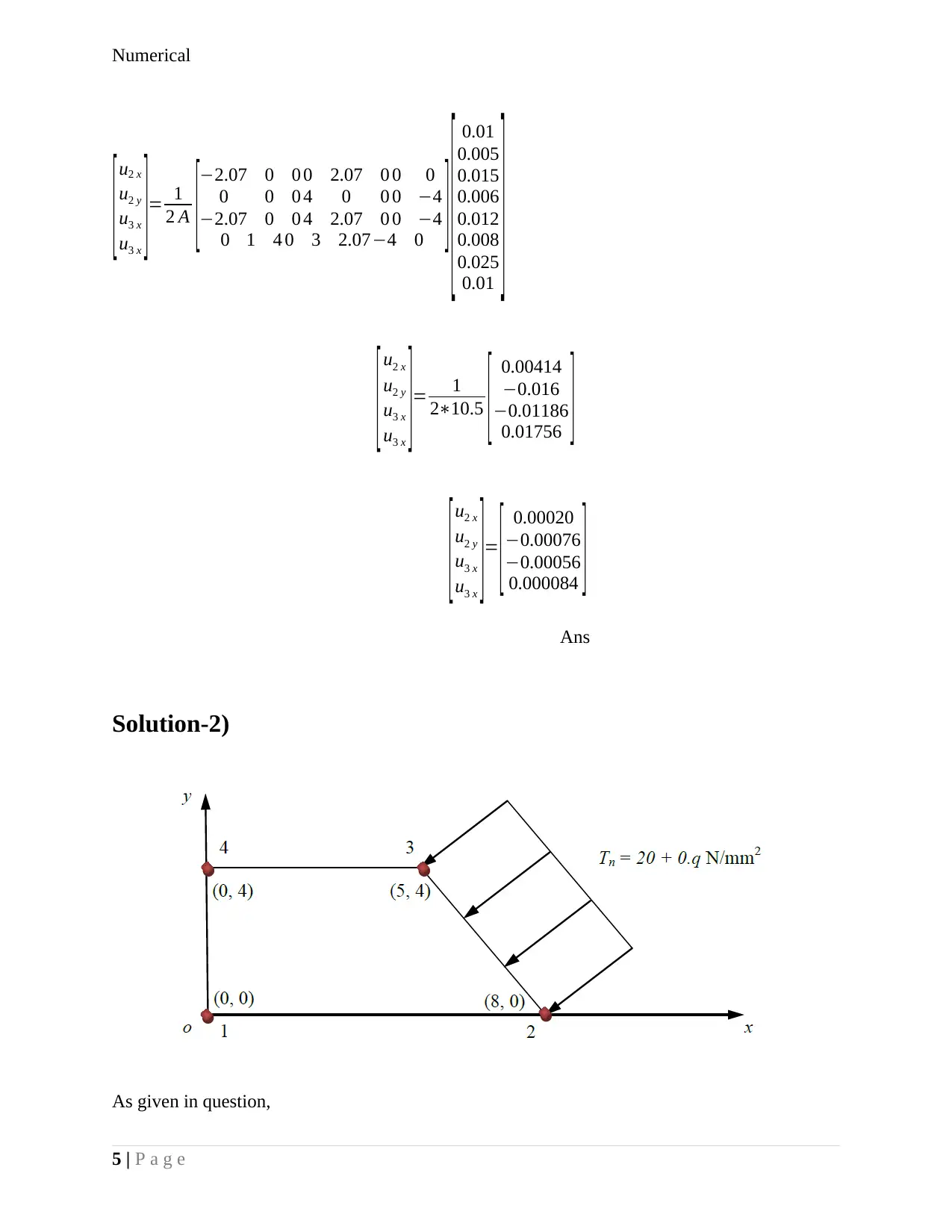










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)