Advanced Mathematics: Calculus and Analysis Homework Solution

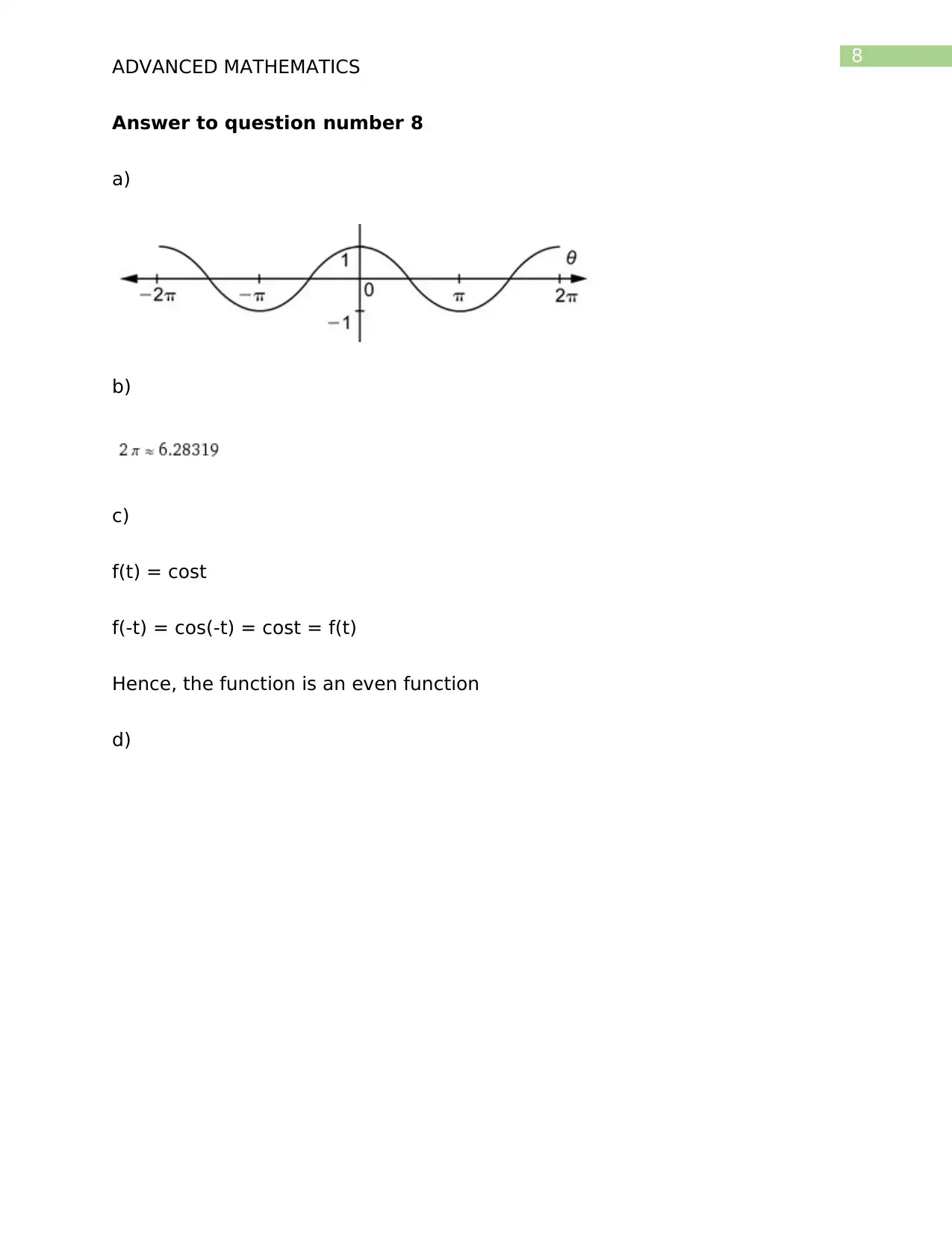
This document presents a comprehensive solution to an advanced mathematics homework assignment. The solution addresses several key concepts in calculus and analysis, including calculating partial derivatives and the equation of a plane, finding critical points of a function, determining local minimums, and the absence of local maxima or saddle points. It also covers double integrals in polar coordinates, solving differential equations, applying integration by parts, determining total differentiability, and identifying even functions. Furthermore, the solution provides step-by-step calculations and explanations for each problem, ensuring clarity and understanding. The assignment covers a range of topics, from basic calculus to more advanced concepts, providing a thorough understanding of the subject matter. The document concludes with a bibliography of relevant academic resources.

Running head: ADVANCED MATHEMATICS
Advanced Mathematics
Name of the Student:
Name of the University:
Author Note

1
ADVANCED MATHEMATICS
Answer to question number 1
Given function:
a)
At first Z0 is to be calculated at (pi/3,2)
Z0 = Z(pi/3,2) = 6
b)
Now partial derivatives are:

2
ADVANCED MATHEMATICS
d/dx = -6.737 = -7 (approx)
d/dy= -2.727 = -3 (approx)
Therefore, the equation of the plane is z = 6 – 7 (x-pi/3) - 3 (y-2) or z = 6-7(x-
1) – 3(y-2) (approx.)
Or, z = -7x -3y + 6 + 7 + 6 Or, z + 7x + 3y -19 = 0
The total Differential at point P is = -7dx -3dy.
Answer to question number 2
The given function is z(x,y) = (e^5(y+1))(4(x^2)-16x+5y+5)
The critical points of the function is (2,2)
It is the local minimum of the function. There are no local maxima and there
is no saddle point.
Answer to question number 3
a)
The given function is V = double integral of xy^2 dxdy
The polar coordinates = double integral of (r cos θ) (r sin θ) ^2 r drdθ

3
ADVANCED MATHEMATICS
x = r cos θ
y = r sin θ
b)

4
ADVANCED MATHEMATICS
c)

5
ADVANCED MATHEMATICS
Answer to question number 4
We know that
y(0) = 0, y'(0) = –1
Answer to question number 5
a)

6
ADVANCED MATHEMATICS
b)
Applying Integration by parts we get
= 2.568 (approx)
Answer to question number 6
a)

7
ADVANCED MATHEMATICS
Hence the function is total differentiable
However,
This function is not total differentiable
b)
U (1,1) =2e
Or, C = -2e -1
Therefore, the actual function is eyx +ex – 2exy + 3x – 2y -2e - 1
Answer to question number 7
Given that, x = cos t, y = sin t, z = tan t.
q (x, y, z) = yx5/81 C/m.
therefore, Q = ∫∫∫ q (x, y, z). dV
= - 0.001

8
ADVANCED MATHEMATICS
Answer to question number 8
a)
b)
c)
f(t) = cost
f(-t) = cos(-t) = cost = f(t)
Hence, the function is an even function
d)

9
ADVANCED MATHEMATICS
e)
f)

10
ADVANCED MATHEMATICS

11
ADVANCED MATHEMATICS
Bibliography
DePountis, V. M., Pogrund, R. L., Griffin-Shirley, N., & Lan, W. Y. (2015).
Technologies Used in the Study of Advanced Mathematics by Students Who
Are Visually Impaired in Classrooms: Teachers' Perspectives. Journal of Visual
Impairment & Blindness, 109(4), 265-278.
Krantz, S. G. (2017). The elements of advanced mathematics. CRC Press.
Lew, K., Fukawa-Connelly, T. P., Mejía-Ramos, J. P., & Weber, K. (2016).
Lectures in advanced mathematics: Why students might not understand
what the mathematics professor is trying to convey. Journal for Research in
Mathematics Education, 47(2), 162-198.
Smith, D., Eggen, M., & Andre, R. S. (2014). A transition to advanced
mathematics. Nelson Education.