ENEM20001 Project: Quad Bike Advanced Modeling, Simulation & Control

This project provides a comprehensive analysis of a quad bike's dynamic behavior, covering single and two-degree-of-freedom systems, as well as ramp modeling. It begins with defining the scope, assumptions, and limitations of the analysis, including payload variations and road conditions. The single-degree-of-freedom (SDOF) analysis focuses on determining suitable suspension stiffness and damping, incorporating free and forced vibration responses, and surface-induced vibration analysis. The two-degree-of-freedom (2DOF) analysis examines vertical mass and vertical pitch, including the impact of non-linearities. MATLAB simulations are used extensively to model and analyze the system's behavior, with comparisons between theoretical calculations and simulation results. The project concludes with a discussion of the findings and their implications for quad bike design and control.

Advanced Modeling, Simulation and Control of Dynamic Systems
Student Name
Student ID Number
Institutional Affiliation
Date of Submission
1

2

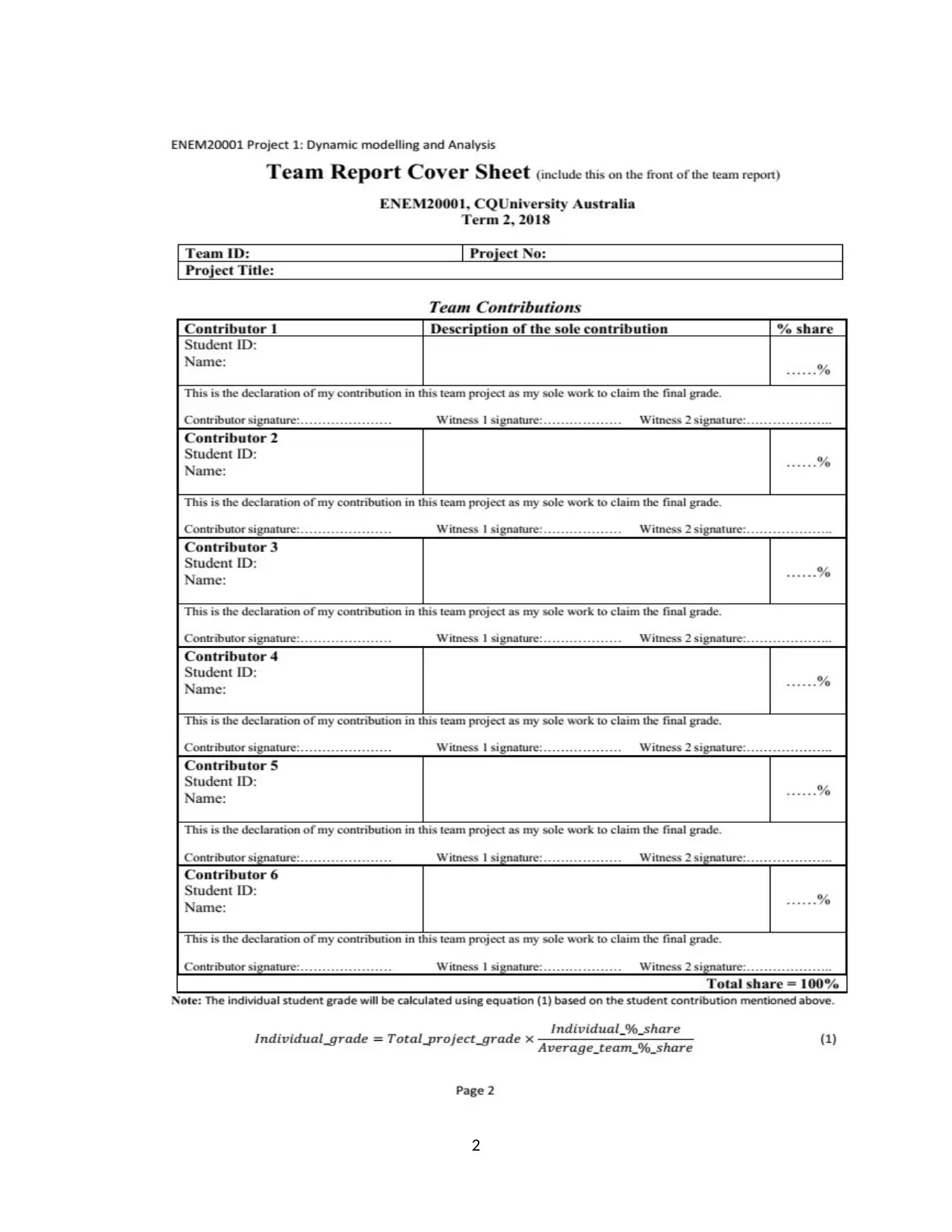
TABLE OF CONTENTS
TABLE OF CONTENTS..........................................................................................................................3
PART A:.....................................................................................................................................................6
PROBLEM SCOPE...............................................................................................................................6
ASSUMPTIONS....................................................................................................................................6
LIMITATIONS.....................................................................................................................................6
QUAD BIKE PAYLOAD DATA VARIATIONS................................................................................6
PART B: SINGLE DEGREE OF FREEDOM........................................................................................7
PART C: TWO-DEGREE OF FREEDOM-VERTICAL TWO MASS..............................................21
PART D: TWO-DEGREE OF FREEDOM-VERTICAL AND PITCH..............................................29
PART E: MODELLING OF RAMP......................................................................................................35
PART F: DISCUSSION AND CONCLUSION.....................................................................................37
REFERENCES........................................................................................................................................38
3

LIST OF FIGURES
Figure 1 Free Body Diagram of Quad Bike plan view [source: sciencedirect.com].......................8
Figure 2 Single Degree of Freedom Quad Bike Simplification using the Mass-spring-damper
system..............................................................................................................................................9
Figure 3 Road Surface induced vibration analysis setup for the SDOF........................................12
Figure 4 The magnification factor of the SDOF- MATLAB implementation [source: MATLAB
r2017b]...........................................................................................................................................13
Figure 5 Transmissibility factor for the SDOF system- MATLAB implementation [Source:
MATLAB r2017b].........................................................................................................................14
Figure 6 System Stability test using the root locus analysis [source: MATLAB r2017b]............15
Figure 7 System Stability illustration using Bode diagram [source: MATLAB r2017b]..............16
Figure 8 MATLAB Simulink for SDOF.......................................................................................18
Figure 9 MATLAB Simulink results for SDOF............................................................................19
Figure 10 MATLAB simulation for SDOF -with non-linearities [source: MATLAB r2017b]....20
Figure 11 MATLAB Simulation results for SDOF -non linearities..............................................20
Figure 13 The System illustration of 2DOF -vertical Mass..........................................................23
Figure 14 Free Body Diagram of the 2DOF system......................................................................23
Figure 15 MATLAB Simulation of 2DOF system for vertical masses.........................................25
Figure 16 MATLAB simulation results for the 2DOF system......................................................26
Figure 17 Illustrating damping relationship of the system in the 2DOF system..........................27
Figure 18 Adding non-linearities to the 2DOF system with vertical mass....................................28
Figure 19 System Results (2DOF with non-linearities)...............................................................29
Figure 22 MATLAB implementation of 2DOF system with vertical pitch..................................31
Figure 23 Illustration of the road surface vibration analysis in 2DOF..........................................32
Figure 24 Adding non-linearities to the MATLAB simulation of 2DOF with vertical pitch........34
Figure 25 Modeling the Quad bike behavior in the ramp test.......................................................35
4

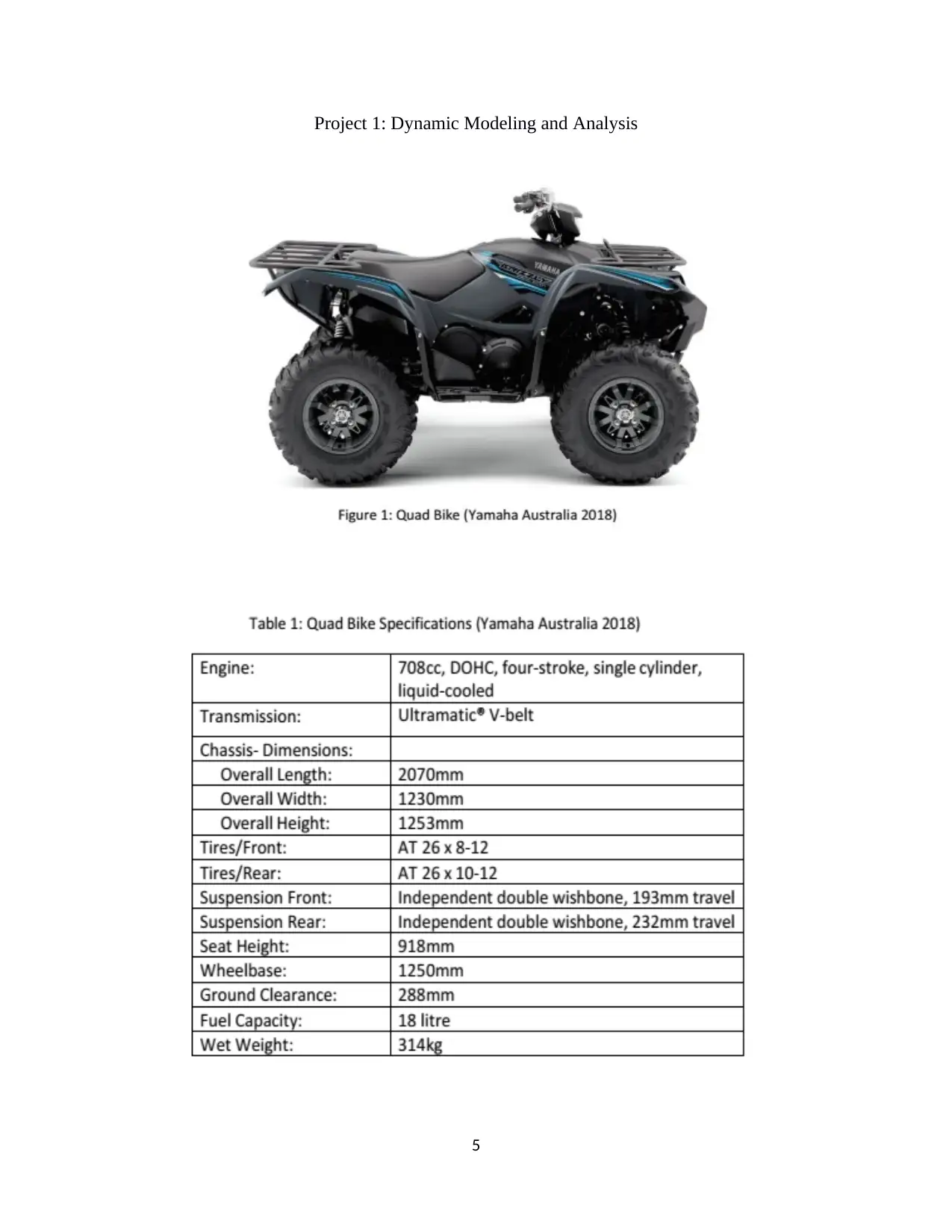
Project 1: Dynamic Modeling and Analysis
5

PART A:
PROBLEM SCOPE
The quad bike analysis seeks to determine the mathematical analysis of the mechanical
aspects of the bike for the single degree of freedom, two degrees of freedom, and the modeling
of the ramp. During analysis, the quad bike is assumed to be implemented on smooth surfaces
with considerable levels of roughness unless where the road roughness is defined. The report
does not focus on the roughness of the road as well as very high degrees of freedom above two
degrees of freedom. Other degrees of freedom are analyzed in other designs to ensure that all
areas that may affect the system.
ASSUMPTIONS
(i) It is assumed that the quad bike has one center of gravity and four wheel of equal height.
(ii) The quad bike has a single rider at every analysis. The chassis and the wheels constitute the
entire weight of the quad bike.
(iii) This is the all-terrain version of Quad bike that operates on the basis of vehicle
propagation for translational and rotary motion. The gravitational acceleration is
given as 9.81 ms-2.
LIMITATIONS
(i) The project is limited to analyzing the quad bike in the single and two-degrees of
freedom.
QUAD BIKE PAYLOAD DATA VARIATIONS
Parameter Value
Rider mass 67 kg (670N)
Payload mass 3140 kg (31400N)
Location Adelaide, Australia
Mass variations 45-56 kg
Road variations 6m ~0.02 m
C1- suspension spring stiffness 25000 (N/m)
B1- suspension absorber damping 1000 (Ns/m)
C2- front axle bellows stiffness 300,000 (N/m)
6

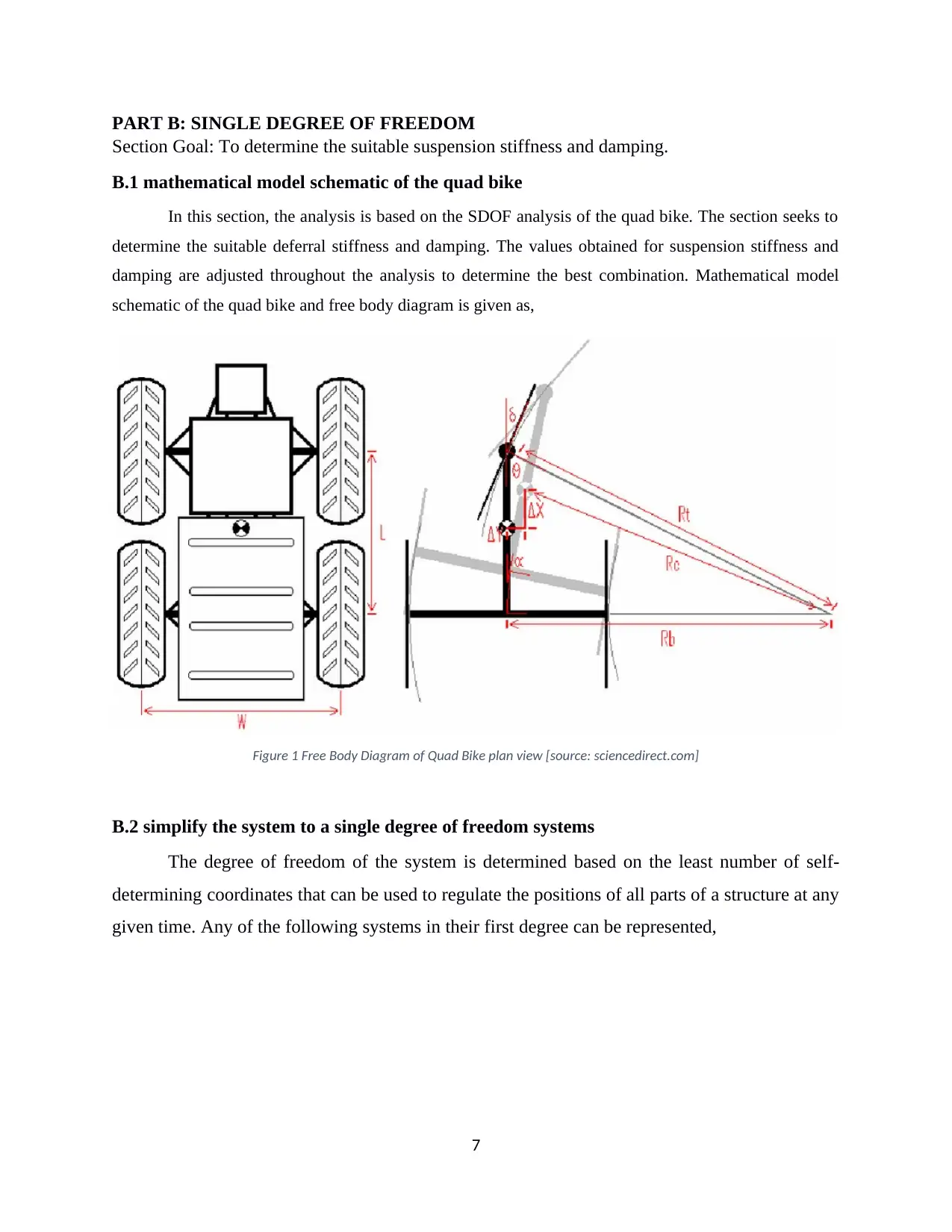
PART B: SINGLE DEGREE OF FREEDOM
Section Goal: To determine the suitable suspension stiffness and damping.
B.1 mathematical model schematic of the quad bike
In this section, the analysis is based on the SDOF analysis of the quad bike. The section seeks to
determine the suitable deferral stiffness and damping. The values obtained for suspension stiffness and
damping are adjusted throughout the analysis to determine the best combination. Mathematical model
schematic of the quad bike and free body diagram is given as,
Figure 1 Free Body Diagram of Quad Bike plan view [source: sciencedirect.com]
B.2 simplify the system to a single degree of freedom systems
The degree of freedom of the system is determined based on the least number of self-
determining coordinates that can be used to regulate the positions of all parts of a structure at any
given time. Any of the following systems in their first degree can be represented,
7

In this project we shall focus on the first illustration, free body diagram, as the single
degree of freedom. Based on the mass-spring-damper system, the resulting equation is given as,
−ω2 mx+ jωcx +kx=F ( appliedforce )
On the road surface, the quad bike is represented such that the resulting equation is given as
shown below,
Fgr ound=Fsdof = jωcx+kx ( damper ∧ spring )
B.3 Draw the 1 DOF free body diagram and write modeling equation
The following is a free body diagram of a single degree of freedom system simplification which
is given as,
Figure 2 Single Degree of Freedom Quad Bike Simplification using the Mass-spring-damper system
The equation of motion, according to Newton’s second law is given as,
m ´r ( t ) +b ´r ( t )+ kr ( t ) =f ( t )
B.4 Analyze the free vibration response for the expected variations in Part A
8

Free vibration is encountered when an initial disturbance leaves a system vibrating on its own
without any external force. A simple pendulum, for instance, can be used to represent the free vibration
after the system is slightly perturbed. When the vibrations cause no energy loss or dissipation due to
friction the vibrations are undamped vibrations. When energy is lost, the result is of damped vibration. In
this instance, the mass spring damper is moved slightly and the free vibration analysis is performed as,
k = EA
l
The spring will deflect to a static equilibrium at a position defined as, δst
W −k ( r +δ st ) =m ´r
The equation of motion is given as,
m ´r +kr =0
It is standardized as,
´r + k
m r=0
The equation results in complex roots whose general solution is given as,
r =e−( ar
2 ) ( Acosωt +Bsinωt )
For an undamped SDOF system is given as,
r ( t ) = Acos ωn t +Bsin ωn t
ωn= √ k
m ( rad
sec )… naturalf requencyofmass
f n= 1
2 π √ k
m ( Hz )
New values of A and B into
r ( t ) =Ccosφcos ωn t +Csinφsinωn t
φ=arctan ( r0
ωn r0 )∧C= √ A2 + B2= √r0
2 +
( ´r0
ωn )2
9

For the undamped case, the free vibration analysis is given as,
m ´r ( t ) +kr ( t ) =f ( t )
It is solved to,
r ( t ) = Asin ωn t+Bcos ωn t … . harmonic
Resonant frequency is obtained as ωn and the natural frequency is obtained as,
ωn= √ k
m
In damped case,
m ´r ( t ) +b ´r ( t )+ kr ( t ) =0
r ( t )= ( A+ Bt ) e−( bt
2 m )
The damping is given as,
b=bcr=2 √ km=2 m ωn
In the under-damped case,
b<bcr
r ( t ) =e
−bt
2 m ( Asinωd t + Bcos ωd t )
ωd=ωn √ 1−ζ2
B.5 Analyze the forced vibration. Assume a small imbalance occurs in the engine
This analysis is carried out when an external force is exerted on the system causing the
system to vibrate. In the instance that the external force links with the natural frequency inherent
to the system, a resonance is said to occur. The result of such resonance is that the system may
10

result in very large oscillations. A harmonic forcing function is applied to the quad bike system
such that,
m ´r ( t ) +b ´r ( t ) +kr ( t ) =psinωt
The equation results into,
r ( t )= p
k
( sinωt+θ
√ (1− ω2
ωn
2 )+ (2 ζω
ωn )2
)
B.6 Analyze the surface induced vibration analysis. Assume road speeds from 0 kph to 50
kph. Assume a simplified corrugation shape and a set of realistic road corrugation depths
and wavelengths.
Figure 3 Road Surface induced vibration analysis setup for the SDOF
y ( t ) = ( 0.01 m ) sin ωb t
With speeds of 0kph to 50 kph
ωb=v km
hr [ 1
3600 ][ hour
3600 s ][ 2 π
cycle ]=0.2909 v rad /s
At 0 kph,
11

ωb ( 0 kph )=0.2909∗0 rad
s =0 rad /s
At 50 kph,
ωb ( 50 kph ) =0.2909∗50 rad /s=14.545 rad /s
B.7 Determine under what conditions resonance may occur and the magnitude effect on the
bike
Determine the frequency and damping ratio of the quad bike suspension,
ωn= √ k
m= √ 6.7∗104
3140 =21.33757 rad / s
ζ = c
2 √ km =
2000 Ns
m
2 √ ( 6.7∗104 ) ( 3140 ) =0.06894
x= ωb
ω = 14.545
11.287 =1.28865
x= yb
√ 1+ ( 2 ζr )2
( 1−r2 )2
+ ( 2 ζr )2
B.8 Produce suitable plots of magnification factor and transmissibility factor for analysis
Suitable magnification factor and transmissibility factor for the single degree of freedom analysis
D= u
us
= 1
√ ( 1−β2 )
2
+ ( 2 βξ ) 2
With a phase angle of,
θ=atan ( 2 ξβ
1−β2 )
The illustration below was performed by the MATLAB,
12