Electrical Power 10 Aerodynamics Compressible Flow Assignment
VerifiedAdded on 2022/11/13
|29
|2945
|489
Homework Assignment
AI Summary
This assignment solution delves into advanced aerodynamics, specifically focusing on compressible flow principles. It explores the behavior of fluids in convergent-divergent nozzles, analyzing stagnation and static temperatures, and the conditions for choked flow. The solution includes detailed calculations for Mach numbers, pressures, temperatures, and velocities in both convergent and divergent sections of nozzles. Furthermore, the assignment examines shock waves and expansion fans, covering adiabatic and isentropic processes, normal and oblique shocks, and their effects on flow parameters. Calculations for shock wave properties, including Mach numbers and pressure ratios, are provided. The assignment also compares different inlet designs for jet engines, evaluating the loss of stagnation pressure to demonstrate the advantages of a weak shock diffuser over a simple inlet configuration. The solution incorporates relevant formulas, tables, and charts to support the calculations and explanations.

Electrical power 1
AERODYNAMICS
Authors Name/s per 1st Affiliation (Author)
Dept. name of the organization
Name of organization, acronyms acceptable
City, Country
mail address
Authors Name/s per 2nd Affiliation (Author)
Dept. name of the organization
Name of organization, acronyms acceptable
City, Country
e-mail address
AERODYNAMICS
Authors Name/s per 1st Affiliation (Author)
Dept. name of the organization
Name of organization, acronyms acceptable
City, Country
mail address
Authors Name/s per 2nd Affiliation (Author)
Dept. name of the organization
Name of organization, acronyms acceptable
City, Country
e-mail address
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Electrical power 2
SECTION 1 – CONVERGENT-DIVERGENT NOZZLES
Question 1.1
Explain the difference between stagnation temperature and static temperature.
[Stagnation temperature is literature reservoir temperature for the stream fluid which is being
measured. In most cases it measured by the help of thermal probe. While the static temperature is that
which is measured through a help of a sensor moving at the same speed of the fluid. In some cases it is
referred to as temperature without velocity effects].
Question 1.2
Under what conditions will the flow through a convergent-divergent nozzle become choked? What
happens to the mass flow rate when exit pressure is decreased on a choked nozzle?
[The fluid flow in the nozzle is chocked due to continues reduction in a back pressure in order to extent
that more reduction is not capable to move the point far from the throat. The mass flow rate will
decrease as the pressure at the exit decrease.]
Question 1.3
If a supersonic flow is run through a convergent duct will its velocity:
a) Decrease
b) Increase
c) Remain constant
d) It depends on the upstream Mach number
e) It depends on the upstream stagnation pressure and temperature.
[Increase]
Question 1.4
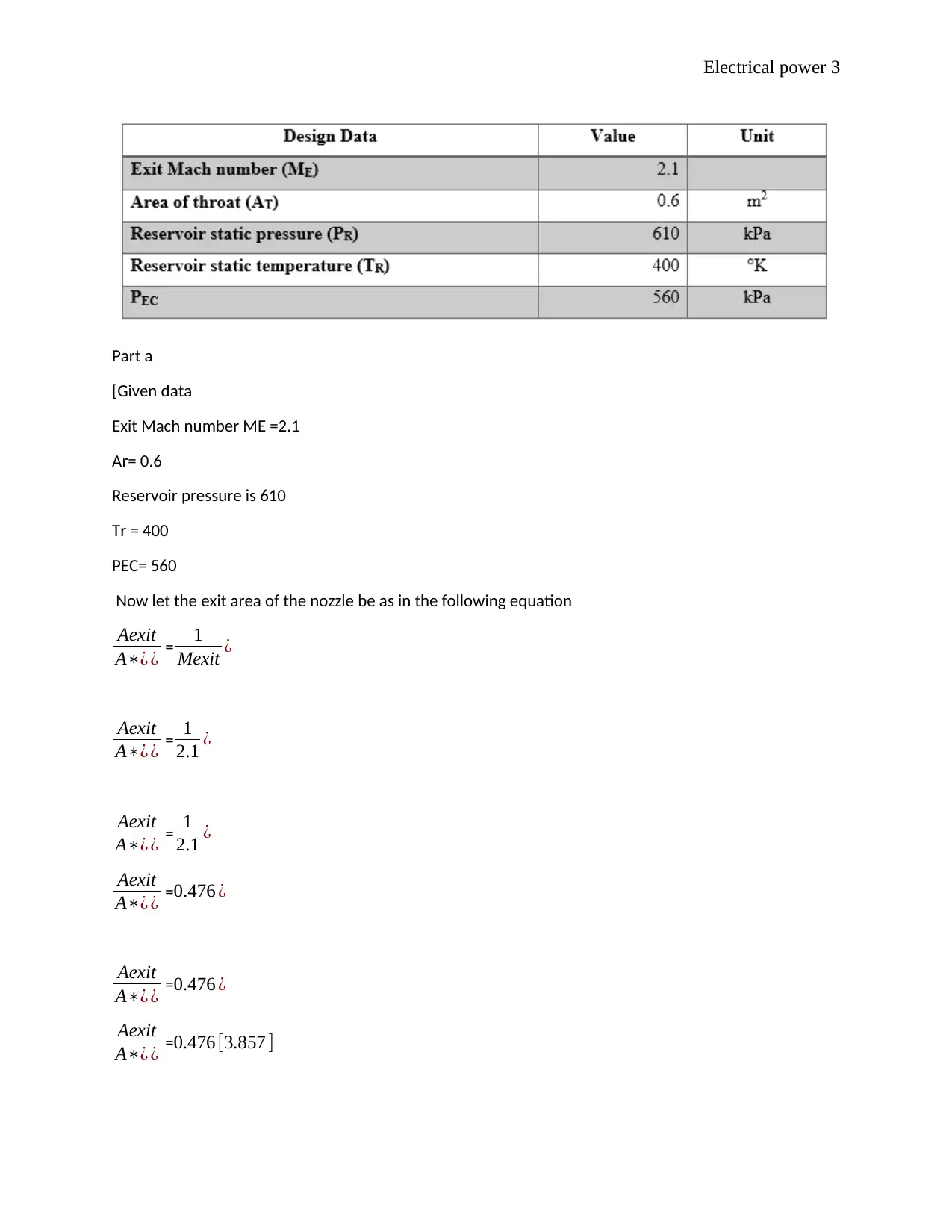
A convergent-divergent nozzle is designed to operate with isentropic flow with an exit Mach number,
ME. The flow in the nozzle is supplied from a reservoir of air with a static pressure of PR and a static
temperature of TR and the nozzle has a throat area, AT, as specified in the table below.
SECTION 1 – CONVERGENT-DIVERGENT NOZZLES
Question 1.1
Explain the difference between stagnation temperature and static temperature.
[Stagnation temperature is literature reservoir temperature for the stream fluid which is being
measured. In most cases it measured by the help of thermal probe. While the static temperature is that
which is measured through a help of a sensor moving at the same speed of the fluid. In some cases it is
referred to as temperature without velocity effects].
Question 1.2
Under what conditions will the flow through a convergent-divergent nozzle become choked? What
happens to the mass flow rate when exit pressure is decreased on a choked nozzle?
[The fluid flow in the nozzle is chocked due to continues reduction in a back pressure in order to extent
that more reduction is not capable to move the point far from the throat. The mass flow rate will
decrease as the pressure at the exit decrease.]
Question 1.3
If a supersonic flow is run through a convergent duct will its velocity:
a) Decrease
b) Increase
c) Remain constant
d) It depends on the upstream Mach number
e) It depends on the upstream stagnation pressure and temperature.
[Increase]
Question 1.4
A convergent-divergent nozzle is designed to operate with isentropic flow with an exit Mach number,
ME. The flow in the nozzle is supplied from a reservoir of air with a static pressure of PR and a static
temperature of TR and the nozzle has a throat area, AT, as specified in the table below.
Electrical power 3
Part a
[Given data
Exit Mach number ME =2.1
Ar= 0.6
Reservoir pressure is 610
Tr = 400
PEC= 560
Now let the exit area of the nozzle be as in the following equation
Aexit
A∗¿ ¿ = 1
Mexit ¿
Aexit
A∗¿ ¿ = 1
2.1 ¿
Aexit
A∗¿ ¿ = 1
2.1 ¿
Aexit
A∗¿ ¿ =0.476 ¿
Aexit
A∗¿ ¿ =0.476 ¿
Aexit
A∗¿ ¿ =0.476 [3.857 ]
Part a
[Given data
Exit Mach number ME =2.1
Ar= 0.6
Reservoir pressure is 610
Tr = 400
PEC= 560
Now let the exit area of the nozzle be as in the following equation
Aexit
A∗¿ ¿ = 1
Mexit ¿
Aexit
A∗¿ ¿ = 1
2.1 ¿
Aexit
A∗¿ ¿ = 1
2.1 ¿
Aexit
A∗¿ ¿ =0.476 ¿
Aexit
A∗¿ ¿ =0.476 ¿
Aexit
A∗¿ ¿ =0.476 [3.857 ]
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Electrical power 4
Aexit
A∗¿ ¿ = 1.726
Part b
Now we calculate the exit area of the nozzle .
Area of throat is AT= 0.6
From Aexit
A∗¿ ¿ = 1.726
Aexit = A* × 1.726
A* = 0.6
Aexit = 0.6 × 1.726
Aexit = 1.03556 m2
Part c
Now we obtain the exit pressure at which the nozzle will become chocked
This is obtained by the use of the following equation
P∗¿
Po ¿=( 2
r +2 ¿
r
r −1
Stagnation pressure / Reseivor static pressure i.e
P∗¿
Po ¿=( 2
3.4 ¿
1.4
1.4−1
P∗¿
Po ¿= 0.15610
P* = 0.15610×610
P* = 95.221 kPa
Part d
The mass flow rate for the exit pressure of 0kpa is
Pexit = 0
So there will be no mass flow rate
M = 0kg/sec
Aexit
A∗¿ ¿ = 1.726
Part b
Now we calculate the exit area of the nozzle .
Area of throat is AT= 0.6
From Aexit
A∗¿ ¿ = 1.726
Aexit = A* × 1.726
A* = 0.6
Aexit = 0.6 × 1.726
Aexit = 1.03556 m2
Part c
Now we obtain the exit pressure at which the nozzle will become chocked
This is obtained by the use of the following equation
P∗¿
Po ¿=( 2
r +2 ¿
r
r −1
Stagnation pressure / Reseivor static pressure i.e
P∗¿
Po ¿=( 2
3.4 ¿
1.4
1.4−1
P∗¿
Po ¿= 0.15610
P* = 0.15610×610
P* = 95.221 kPa
Part d
The mass flow rate for the exit pressure of 0kpa is
Pexit = 0
So there will be no mass flow rate
M = 0kg/sec
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Electrical power 5
Part e
Now we obtain the mass flow rate for exit pressure of 560k Pa
We have mi= P0Mexit A √ r
RT 0 (1+ r−1
2 ) M 2 ¿
r+1
2(r−1)
After substitution we obtain the following;
M= 610× 1.03556×2 √ 1.4
8.314 ×400 [(1+ 0.4
2 ) 2.12 ¿ ¿¿−3
M= 1263.38 × 0.02051 × [5.292 ¿−3
M= 1263.38 × 0.02051 ×0.0067474
M= 0.17483 kg / Sec
Question 1.5
A small supersonic wind tunnel, consists of a convergent-divergent nozzle designed to be operated using
a bottle of compressed helium gas (γ = 5/3, R = 2.077 kJ/kg/°K). The test section has a diameter, d, and
the tunnel is designed to operate at Mach number, M, with a static pressure, P, and a static
temperature, T, specified in the table below.
Part e
Now we obtain the mass flow rate for exit pressure of 560k Pa
We have mi= P0Mexit A √ r
RT 0 (1+ r−1
2 ) M 2 ¿
r+1
2(r−1)
After substitution we obtain the following;
M= 610× 1.03556×2 √ 1.4
8.314 ×400 [(1+ 0.4
2 ) 2.12 ¿ ¿¿−3
M= 1263.38 × 0.02051 × [5.292 ¿−3
M= 1263.38 × 0.02051 ×0.0067474
M= 0.17483 kg / Sec
Question 1.5
A small supersonic wind tunnel, consists of a convergent-divergent nozzle designed to be operated using
a bottle of compressed helium gas (γ = 5/3, R = 2.077 kJ/kg/°K). The test section has a diameter, d, and
the tunnel is designed to operate at Mach number, M, with a static pressure, P, and a static
temperature, T, specified in the table below.

Electrical power 6
T 0
T = 1+ ( r−1
2 ¿ m2
P 0
P = [1+( r−1
2 ¿ m2 ¿
r
r−1
ρ 0
ρ = [1++( r−1
2 ¿ m2 ¿
r
r−1
At the given dimension
⍴= ρ
RT = 30× 1000
2077 ×185 = 30000
384245 = 0.0780kg/m3
Part a
m=⍴ AV = ⍴ ( π d2
4 )m√rRT
m= 0.0780 ( π 152 10−6
4 ) 1.5 √ 5
3 ×2.077 ×100017.5
m= 1.61
Part b
Area = A/At = 1/m ( 2+(r −1)( m2 )
r +1 ) r +1
2(r−1)
π ( 152 )
4
π ( d t2 )
4
= 1
1.5 ( 2+ ( 1.667−1 ) (1. 52 )
1.6667+1 ¿
1.6667+ 1
1.6667−1¿ ¿
152
d t2 = 1.1483 or simply
dt= 13.997≅ 14 mm
T 0
T = 1+ ( r−1
2 ¿ m2
P 0
P = [1+( r−1
2 ¿ m2 ¿
r
r−1
ρ 0
ρ = [1++( r−1
2 ¿ m2 ¿
r
r−1
At the given dimension
⍴= ρ
RT = 30× 1000
2077 ×185 = 30000
384245 = 0.0780kg/m3
Part a
m=⍴ AV = ⍴ ( π d2
4 )m√rRT
m= 0.0780 ( π 152 10−6
4 ) 1.5 √ 5
3 ×2.077 ×100017.5
m= 1.61
Part b
Area = A/At = 1/m ( 2+(r −1)( m2 )
r +1 ) r +1
2(r−1)
π ( 152 )
4
π ( d t2 )
4
= 1
1.5 ( 2+ ( 1.667−1 ) (1. 52 )
1.6667+1 ¿
1.6667+ 1
1.6667−1¿ ¿
152
d t2 = 1.1483 or simply
dt= 13.997≅ 14 mm
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Electrical power 7
Part C
T0= 185 (1+ m2
3 )
T0 = 185 (1+ 1.52
3 )
T0= 323.75 K
Part d
Pressure P 0 = 30 (1+ 1.52
3 ¿2.5
Pressure = 121.54kPa
Question 1.6
A convergent-divergent nozzle is attached to a reservoir of air at a temperature, TR, and a pressure, PR,
as defined in the table below. Assuming the flow is supersonic in the divergent section, then calculate
the Mach number, pressure, temperature and velocity for the value of A/A* specified in the table, at the
location (a) in the convergent section, and (b) in the divergent section.
Part a
From the given data
Tr = 310
Pr= 205
A/A*= 3
i. Mach Number
A/A*=3
Part C
T0= 185 (1+ m2
3 )
T0 = 185 (1+ 1.52
3 )
T0= 323.75 K
Part d
Pressure P 0 = 30 (1+ 1.52
3 ¿2.5
Pressure = 121.54kPa
Question 1.6
A convergent-divergent nozzle is attached to a reservoir of air at a temperature, TR, and a pressure, PR,
as defined in the table below. Assuming the flow is supersonic in the divergent section, then calculate
the Mach number, pressure, temperature and velocity for the value of A/A* specified in the table, at the
location (a) in the convergent section, and (b) in the divergent section.
Part a
From the given data
Tr = 310
Pr= 205
A/A*= 3
i. Mach Number
A/A*=3
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Electrical power 8
For the relation A/A* = 1
m [( 2
k +1 ¿ ¿
The value of k is assumed to be 1.4
3= 1
m [( 2
1.4+1 ¿ ¿
3= 1
m [(0.833 ¿ ¿
31/3= 1
m
1/3 [(0.833+0.16667 m2 ¿31/3
1.444m1/3 = [(0.833+0.16667 m2 ¿
1.444m1/3 -0.16667 m2= 0.833
M= 2.625
ii.
For A/A*=3
Thus P
P 0 = 21.557 ( From the table)
P= 21.557 ×P0
P= 21.557 ×205
P= 4419.185 kPa
iii.
For A/A*=3
T
T 0 = 2.4045 (from the table )
T=2.4045 × T0
T=2.4045 × 310
T= 745.395K
iv.
Velocity V1 = M x velocity of sound at 310 K
For the relation A/A* = 1
m [( 2
k +1 ¿ ¿
The value of k is assumed to be 1.4
3= 1
m [( 2
1.4+1 ¿ ¿
3= 1
m [(0.833 ¿ ¿
31/3= 1
m
1/3 [(0.833+0.16667 m2 ¿31/3
1.444m1/3 = [(0.833+0.16667 m2 ¿
1.444m1/3 -0.16667 m2= 0.833
M= 2.625
ii.
For A/A*=3
Thus P
P 0 = 21.557 ( From the table)
P= 21.557 ×P0
P= 21.557 ×205
P= 4419.185 kPa
iii.
For A/A*=3
T
T 0 = 2.4045 (from the table )
T=2.4045 × T0
T=2.4045 × 310
T= 745.395K
iv.
Velocity V1 = M x velocity of sound at 310 K

Electrical power 9
(1.27)×√ rRT
V1= 2.625 √1.4 ×287310
V1=2.625 √ 1124558
V1=2.625 ×352.92
V1= 926.41 m/s
Part b
Divergent part
For a flow to be super sank at all divergent part maximum mach number that it can realize at a flow
which is equal to 1.
i. Mach number M2 = M 12 (k +1)
2(k −1) M 12
M1 = 2.625
16.53
5.5125 = M2
M2= 2.998
M2≈ 3
ii.
Now P
Pdiv = ( 1+ k−1
2 )M2
P
Pdiv = 1+( 1+ 0.4
2 ) 9
P
Pdiv = 11.8
Pdiv = 11.8
2.392
Pdiv = 4.933 kPa
iii.
M= 3
Tdiv
Tinlet =0.417
(1.27)×√ rRT
V1= 2.625 √1.4 ×287310
V1=2.625 √ 1124558
V1=2.625 ×352.92
V1= 926.41 m/s
Part b
Divergent part
For a flow to be super sank at all divergent part maximum mach number that it can realize at a flow
which is equal to 1.
i. Mach number M2 = M 12 (k +1)
2(k −1) M 12
M1 = 2.625
16.53
5.5125 = M2
M2= 2.998
M2≈ 3
ii.
Now P
Pdiv = ( 1+ k−1
2 )M2
P
Pdiv = 1+( 1+ 0.4
2 ) 9
P
Pdiv = 11.8
Pdiv = 11.8
2.392
Pdiv = 4.933 kPa
iii.
M= 3
Tdiv
Tinlet =0.417
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Electrical power 10
Tdiv = 0.417×745.395
Tdiv= 310.8 K
iv.
Velocity = 2.625 √ 1.4 ×287 × 310
Velocity 2.625 √124558
V= 926.43 m/s
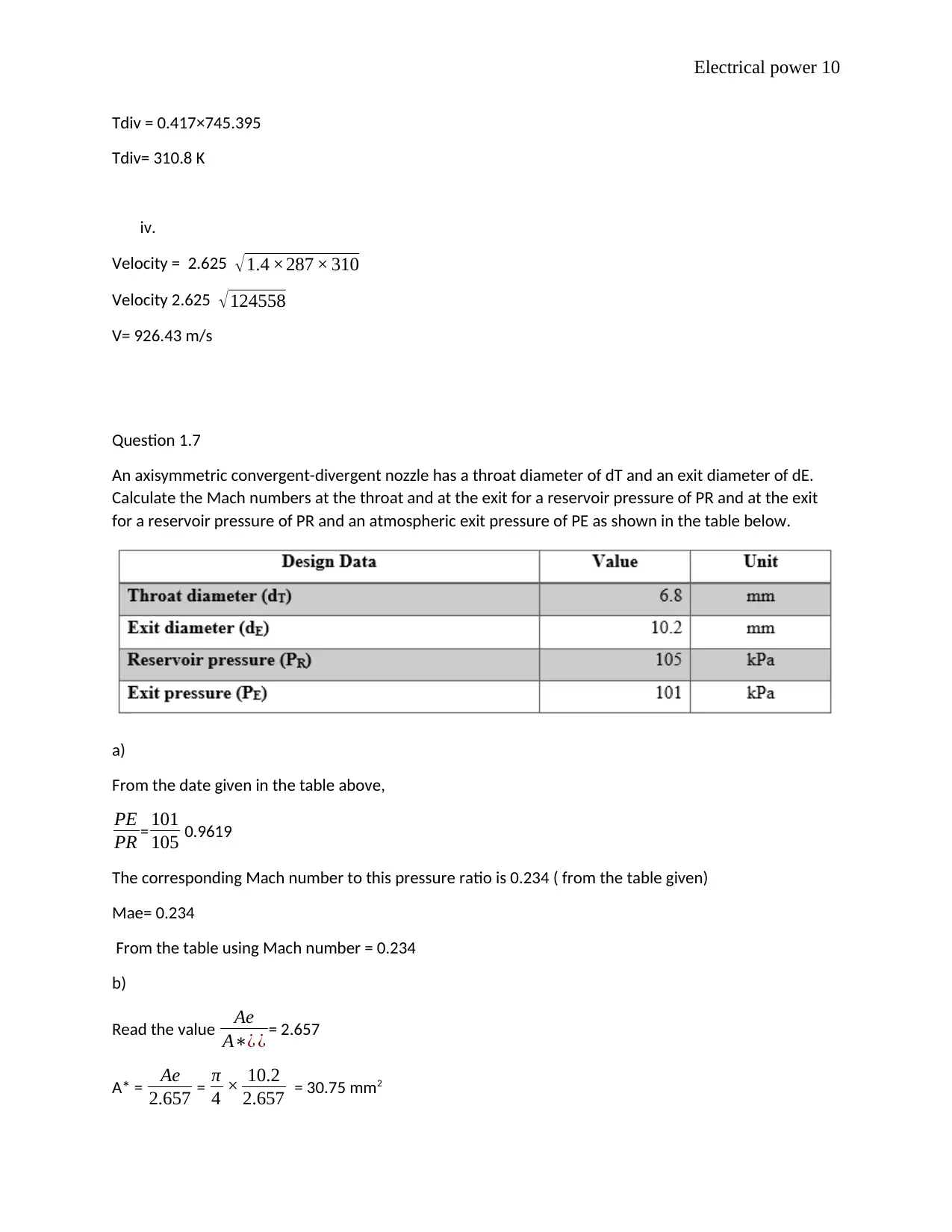
Question 1.7
An axisymmetric convergent-divergent nozzle has a throat diameter of dT and an exit diameter of dE.
Calculate the Mach numbers at the throat and at the exit for a reservoir pressure of PR and at the exit
for a reservoir pressure of PR and an atmospheric exit pressure of PE as shown in the table below.
a)
From the date given in the table above,
PE
PR = 101
105 0.9619
The corresponding Mach number to this pressure ratio is 0.234 ( from the table given)
Mae= 0.234
From the table using Mach number = 0.234
b)
Read the value Ae
A∗¿ ¿ = 2.657
A* = Ae
2.657 = π
4 × 10.2
2.657 = 30.75 mm2
Tdiv = 0.417×745.395
Tdiv= 310.8 K
iv.
Velocity = 2.625 √ 1.4 ×287 × 310
Velocity 2.625 √124558
V= 926.43 m/s
Question 1.7
An axisymmetric convergent-divergent nozzle has a throat diameter of dT and an exit diameter of dE.
Calculate the Mach numbers at the throat and at the exit for a reservoir pressure of PR and at the exit
for a reservoir pressure of PR and an atmospheric exit pressure of PE as shown in the table below.
a)
From the date given in the table above,
PE
PR = 101
105 0.9619
The corresponding Mach number to this pressure ratio is 0.234 ( from the table given)
Mae= 0.234
From the table using Mach number = 0.234
b)
Read the value Ae
A∗¿ ¿ = 2.657
A* = Ae
2.657 = π
4 × 10.2
2.657 = 30.75 mm2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Electrical power 11
AT
A∗¿ ¿ =
π
4 × dT
A∗¿ ¿
=
π
4 × 6.82
30.75
= 1.18
This corresponding to AT/A* = 1.18 the value of Mach number is 0.6
SECTION 2 – SHOCK WAVES AND EXPANSION FANS
Question 2.1
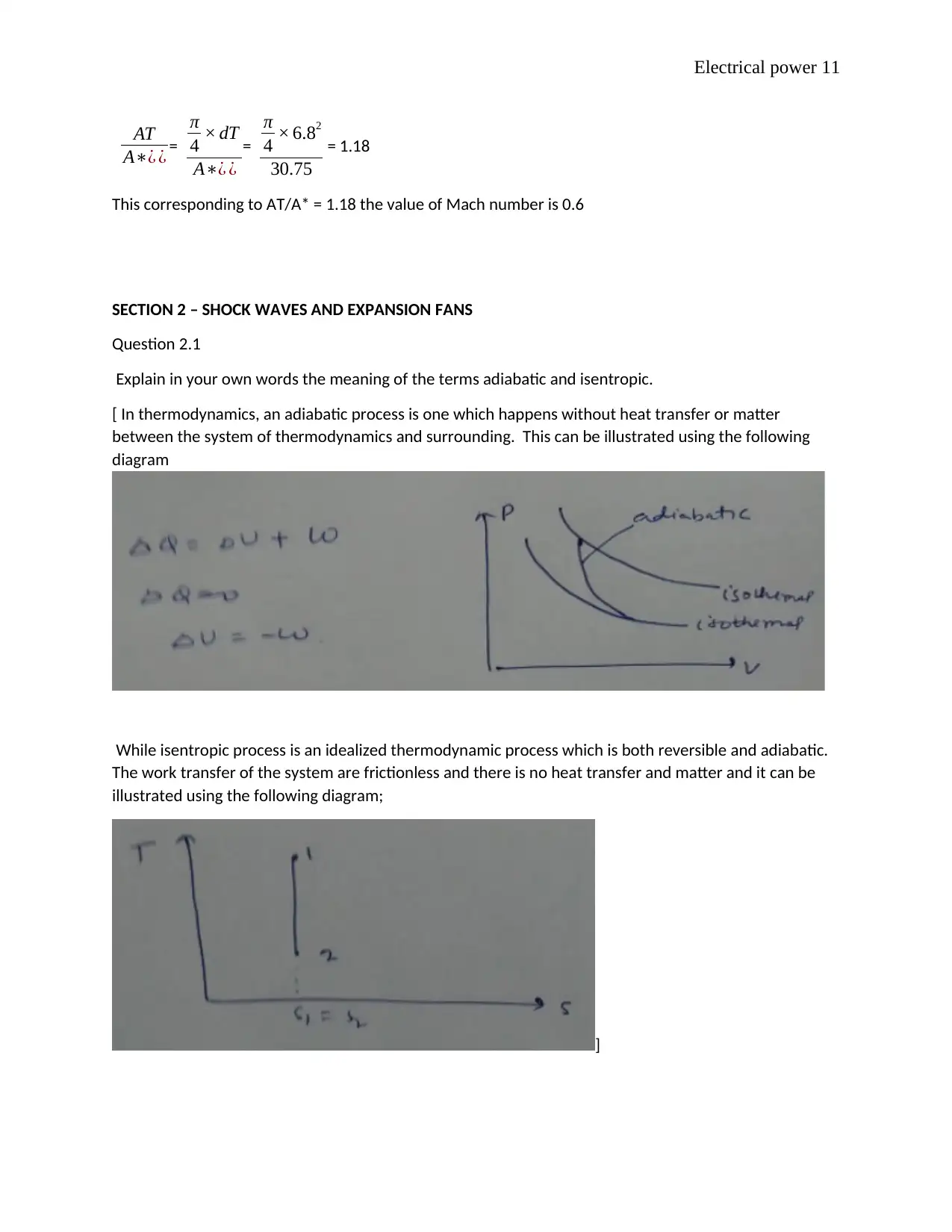
Explain in your own words the meaning of the terms adiabatic and isentropic.
[ In thermodynamics, an adiabatic process is one which happens without heat transfer or matter
between the system of thermodynamics and surrounding. This can be illustrated using the following
diagram
While isentropic process is an idealized thermodynamic process which is both reversible and adiabatic.
The work transfer of the system are frictionless and there is no heat transfer and matter and it can be
illustrated using the following diagram;
]
AT
A∗¿ ¿ =
π
4 × dT
A∗¿ ¿
=
π
4 × 6.82
30.75
= 1.18
This corresponding to AT/A* = 1.18 the value of Mach number is 0.6
SECTION 2 – SHOCK WAVES AND EXPANSION FANS
Question 2.1
Explain in your own words the meaning of the terms adiabatic and isentropic.
[ In thermodynamics, an adiabatic process is one which happens without heat transfer or matter
between the system of thermodynamics and surrounding. This can be illustrated using the following
diagram
While isentropic process is an idealized thermodynamic process which is both reversible and adiabatic.
The work transfer of the system are frictionless and there is no heat transfer and matter and it can be
illustrated using the following diagram;
]

Electrical power 12
Question 2.2
Which of the following is true of a normal shock?
a) Downstream M will depend on upstream M, p, and T.
b) Downstream M will depend only on upstream p and T.
c) Downstream p and T will depend only on upstream M.
d) Downstream T will depend only on upstream T.
e) None of the above
[Downstream p and T will depend only on upstream M.]
Question 2.3
Which of the following is true of flow across an expansion wave?
a) p0 and T0 will both increase.
b) p0 will increase while T0 will decrease.
c) p0 will decrease while T0 will increase.
d) p0 and T0 will both decrease
e) p0 and T0 will both remain constant
[p0 and T0 will both decrease]
Question 2.4
Which of the following is true of a supersonic flow past a wedge?
[Increasing wedge angle will increase the chance of shock detaching]
Question 2.5
A normal shock is located inside the divergent section of a convergent-divergent nozzle at a location
where the ratio of duct area to throat area is specified in the table below. Given the exit area to throat
area ratio specified in the table below, calculate the following quantities.
From the data given in the table above;
i.
Question 2.2
Which of the following is true of a normal shock?
a) Downstream M will depend on upstream M, p, and T.
b) Downstream M will depend only on upstream p and T.
c) Downstream p and T will depend only on upstream M.
d) Downstream T will depend only on upstream T.
e) None of the above
[Downstream p and T will depend only on upstream M.]
Question 2.3
Which of the following is true of flow across an expansion wave?
a) p0 and T0 will both increase.
b) p0 will increase while T0 will decrease.
c) p0 will decrease while T0 will increase.
d) p0 and T0 will both decrease
e) p0 and T0 will both remain constant
[p0 and T0 will both decrease]
Question 2.4
Which of the following is true of a supersonic flow past a wedge?
[Increasing wedge angle will increase the chance of shock detaching]
Question 2.5
A normal shock is located inside the divergent section of a convergent-divergent nozzle at a location
where the ratio of duct area to throat area is specified in the table below. Given the exit area to throat
area ratio specified in the table below, calculate the following quantities.
From the data given in the table above;
i.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 29
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


