AFIN270 Assignment: Financial Modeling, Analysis, and Statistics

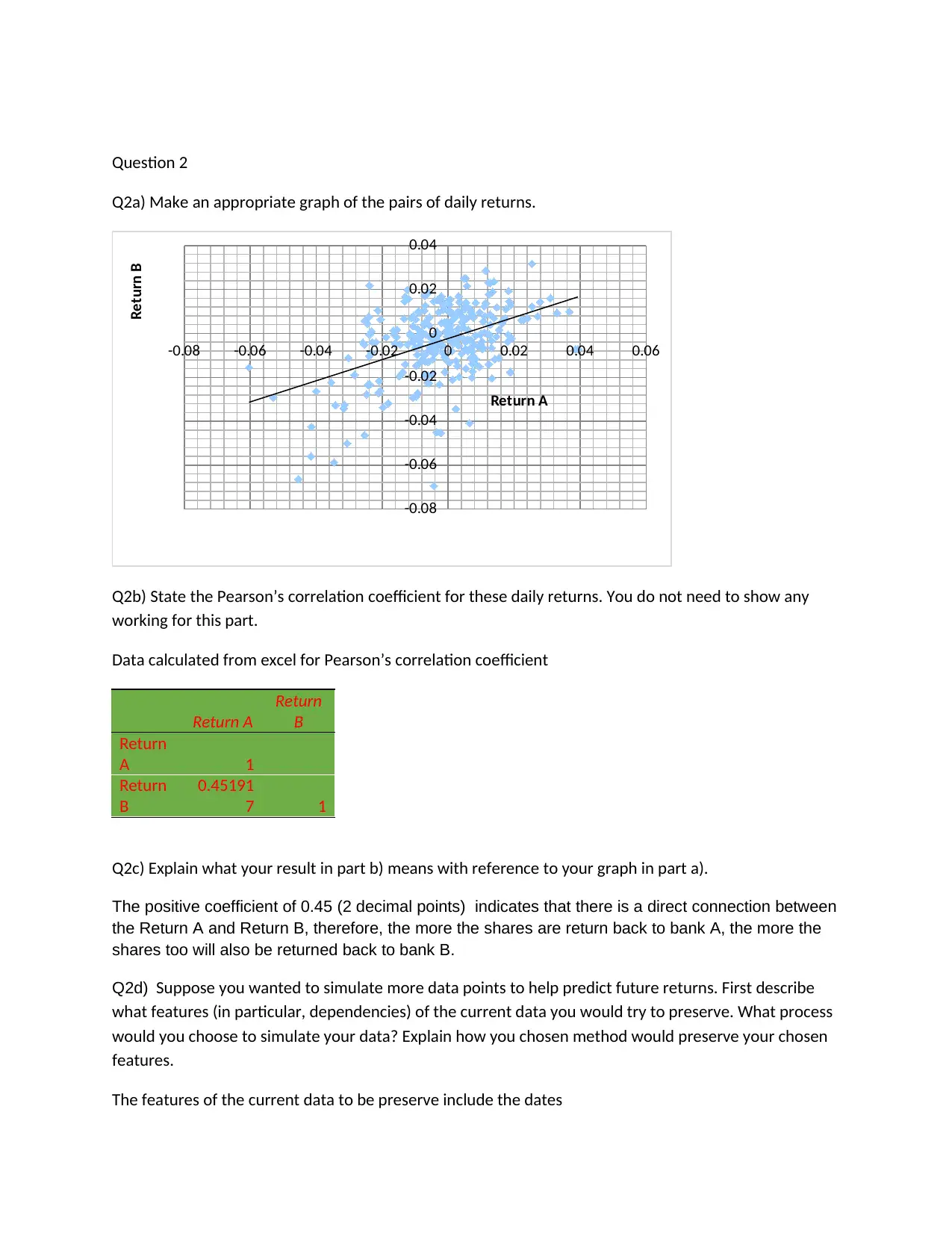
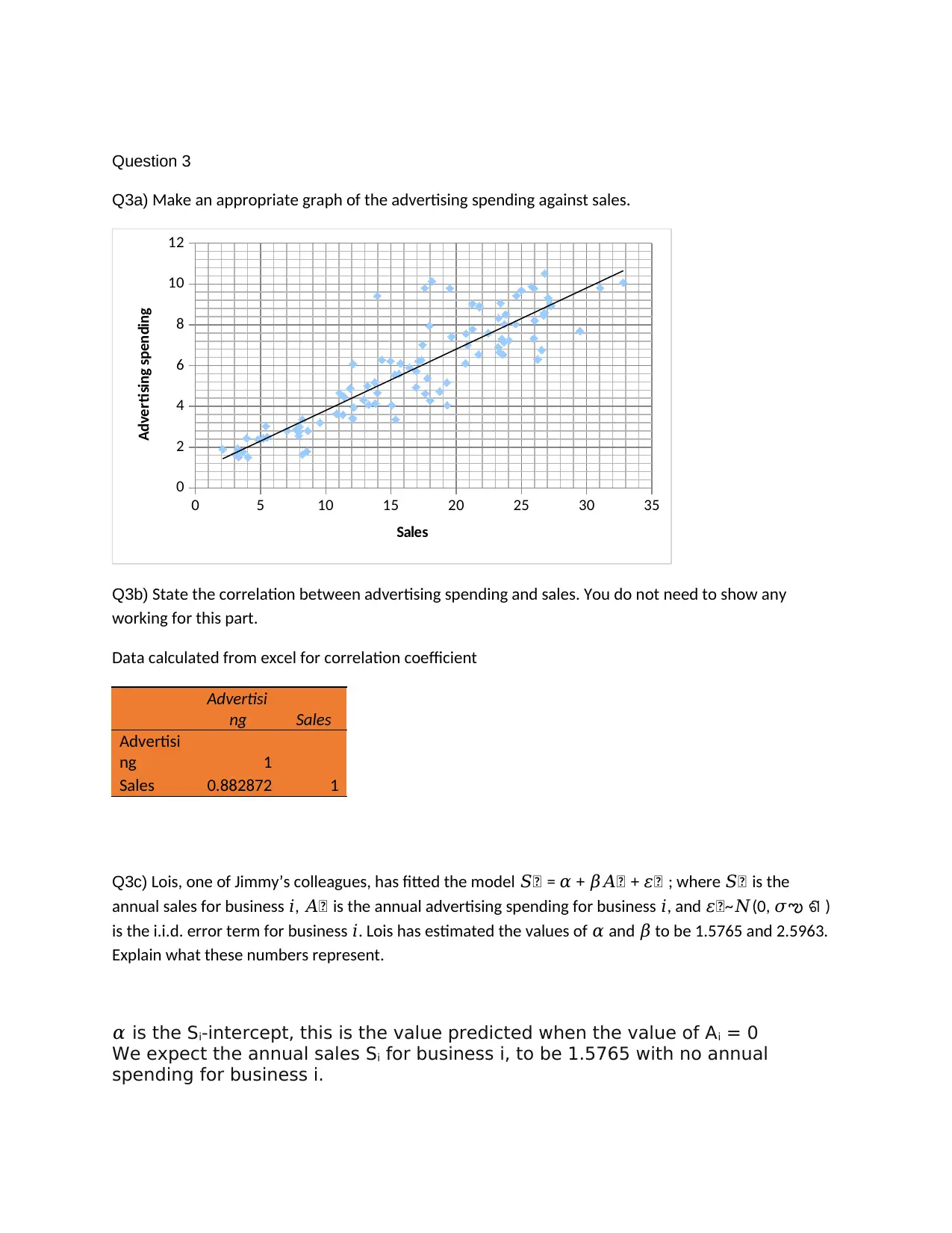
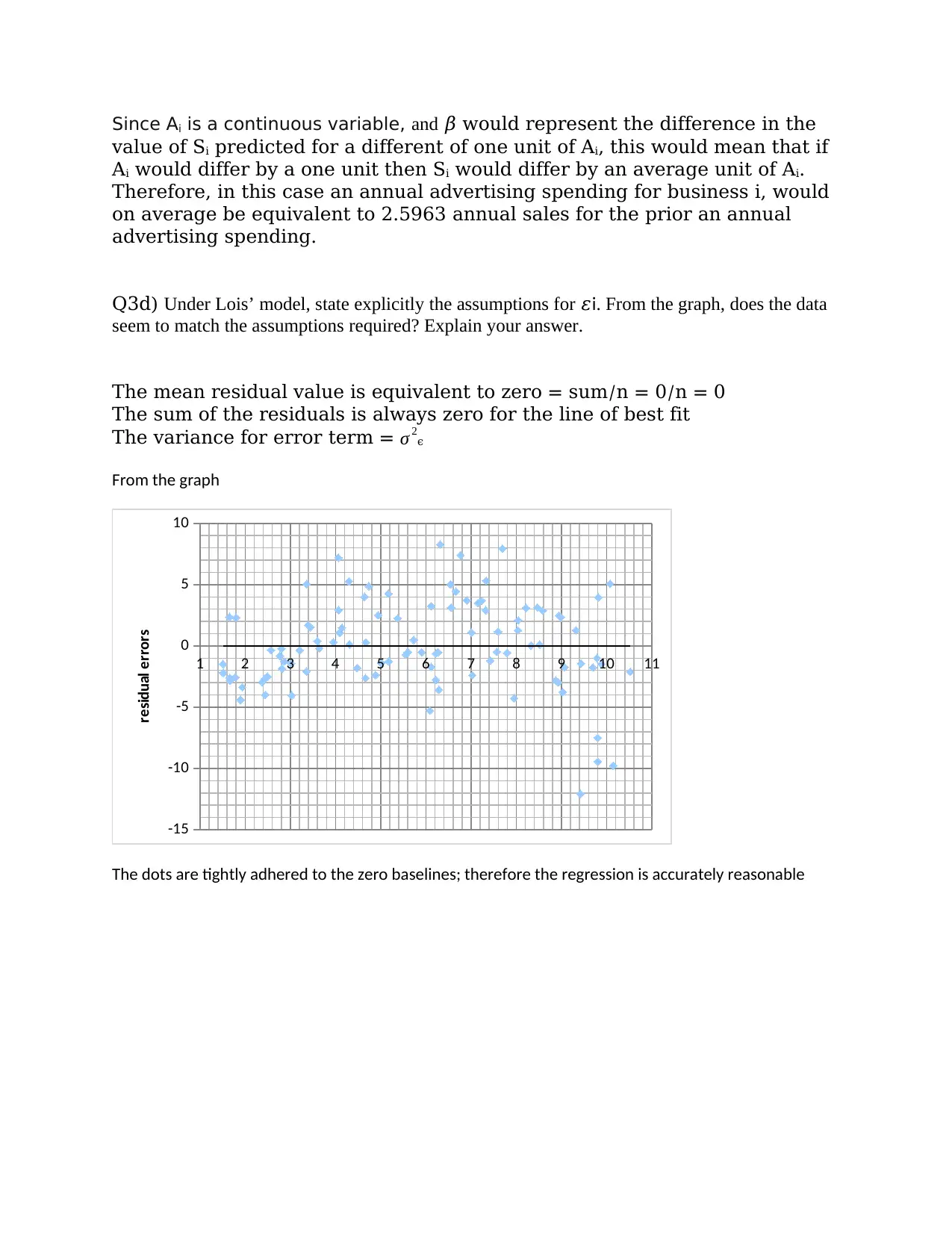
This document presents a comprehensive solution to an AFIN270 finance assignment. The solution addresses various aspects of financial modeling and statistical analysis. The assignment includes questions on probability, such as constructing a duty migration table and calculating probabilities related to guard assignments in Camelot. It also covers correlation analysis, requiring the calculation and interpretation of Pearson's correlation coefficient, as well as the creation of graphs to visualize the relationship between daily returns. Further, the assignment explores regression analysis, including interpreting regression coefficients and assessing model assumptions. Finally, the document provides a solution to a problem involving the Fréchet distribution, requiring the calculation of probabilities using the cumulative distribution function. The solution demonstrates a strong understanding of financial concepts and statistical techniques.

Question 1
Q1a) Write down a “duty migration table” containing the probabilities listed above.
Royal Battlement Peace
Royal family 0.7 0.3 0
Battlement 0.4 0 0.6
Peace 0.1 0.4 0.5
Q1b) Peter is a guard currently assigned to peace keeping. However, Peter has a fear of heights and thus
does not enjoy patrolling the battlements. What is the probability that he will NOT have to patrol the
battlements at all within the following 2 weeks?
0.1 R
1/3 0.9 NR
1/3 0.4 B
1/3 0.6 NR
0.5 P
0.5
NP
Note;
R = royal family
NR = not reassigned to royal family
B = Battlement
NB = not reassigned to battlement
P = Peace
NP = not reassigned to peace

P(Not reassigned to patrol battlement) = 1/3*0.6 = 0.2
Q1c) Gambit is another guard, currently assigned to protect the royal family. As an avid gambler, Gambit
has made a bet with some of the other guards. He has made a bet based on where he will be assigned in
2 weeks’ time, with the following payoffs:
What is the expected payoff for Gambit, given the information above?
Duty Royal Battlement Peace
Bet $5 $2 $1
Probability Royal family 0.7 0.3 0
Expected payoff = ∑ piXi
= 0.7 *$5 + 0.3*$2 + 0*$1 = $4.10

Question 2
Q2a) Make an appropriate graph of the pairs of daily returns.
-0.08 -0.06 -0.04 -0.02 0 0.02 0.04 0.06
-0.08
-0.06
-0.04
-0.02
0
0.02
0.04
Return A
Return B
Q2b) State the Pearson’s correlation coefficient for these daily returns. You do not need to show any
working for this part.
Data calculated from excel for Pearson’s correlation coefficient
Return A
Return
B
Return
A 1
Return
B
0.45191
7 1
Q2c) Explain what your result in part b) means with reference to your graph in part a).
The positive coefficient of 0.45 (2 decimal points) indicates that there is a direct connection between
the Return A and Return B, therefore, the more the shares are return back to bank A, the more the
shares too will also be returned back to bank B.
Q2d) Suppose you wanted to simulate more data points to help predict future returns. First describe
what features (in particular, dependencies) of the current data you would try to preserve. What process
would you choose to simulate your data? Explain how you chosen method would preserve your chosen
features.
The features of the current data to be preserve include the dates

The approach used is called Monte Carlo simulation
To generate the random numbers in excel we use the two functions
1. RAND ( ): generating random numbers from 0 and 1
2. RANDBETWEEN(a, b): generating random numbers from the integers between a and b
To avoid the random numbers generated from changing on excel we enter RAND ( ) on the bar
formula and press the key function F9. Similarly, copy the random numbers generated using Ctrl-C
and paste on the same location.
RANDBETWEEN would only generate integer values.

Question 3
Q3a) Make an appropriate graph of the advertising spending against sales.
0 5 10 15 20 25 30 35
0
2
4
6
8
10
12
Sales
Advertising spending
Q3b) State the correlation between advertising spending and sales. You do not need to show any
working for this part.
Data calculated from excel for correlation coefficient
Advertisi
ng Sales
Advertisi
ng 1
Sales 0.882872 1
Q3c) Lois, one of Jimmy’s colleagues, has fitted the model 𝑆௜ = 𝛼 + 𝛽𝐴௜ + 𝜀௜ ; where 𝑆௜ is the
annual sales for business 𝑖, 𝐴௜ is the annual advertising spending for business 𝑖, and 𝜀௜~𝑁(0, 𝜎ఌ ଶ )
is the i.i.d. error term for business 𝑖. Lois has estimated the values of 𝛼 and 𝛽 to be 1.5765 and 2.5963.
Explain what these numbers represent.
𝛼 is the Si-intercept, this is the value predicted when the value of Ai = 0
We expect the annual sales Si for business i, to be 1.5765 with no annual
spending for business i.

Since Ai is a continuous variable, and 𝛽 would represent the difference in the
value of Si predicted for a different of one unit of Ai, this would mean that if
Ai would differ by a one unit then Si would differ by an average unit of Ai.
Therefore, in this case an annual advertising spending for business i, would
on average be equivalent to 2.5963 annual sales for the prior an annual
advertising spending.
Q3d) Under Lois’ model, state explicitly the assumptions for 𝜀i. From the graph, does the data
seem to match the assumptions required? Explain your answer.
The mean residual value is equivalent to zero = sum/n = 0/n = 0
The sum of the residuals is always zero for the line of best fit
The variance for error term = σ 2ϵ
From the graph
1 2 3 4 5 6 7 8 9 10 11
-15
-10
-5
0
5
10
residual errors
The dots are tightly adhered to the zero baselines; therefore the regression is accurately reasonable

Question 4
Q4) Clint is modelling the monthly returns for shares in Stork Industrial using a Fréchet distribution. He
believes the return 𝑅 follows a 𝐺𝐸(0.03,0.02,0.015) distribution.
a) Write down the CDF for this distribution, and then state clearly what this function represents.
The cumulative distribution function of a GEV is
F(R; μ , δ , ϵ ¿=exp {−
[1+ϵ ( x−N
δ ) ]−1
ϵ
F(R; 0.03, 0.02, 0.015) = exp {− [ 1+ 0.015 ( R−0.03
0.02 ) ] −1
0.015
= e− [1 +0.015 ( R −0.03
0.02 )] −1
0.015
b) Using part a) or otherwise, calculate Pr(𝑅 > 10%). Show all steps of working.
Pr(R > 10%)
= 1 – p( ≤ 0.1¿
= 1 - e− [1 +0.015 ( 0.1−0.03
0.02 ) ] −1
0.015
= 1 – 0.3679 = 0.6321