Programming Assignment: AI Algorithms (A*, Hill Climbing, RBFS)

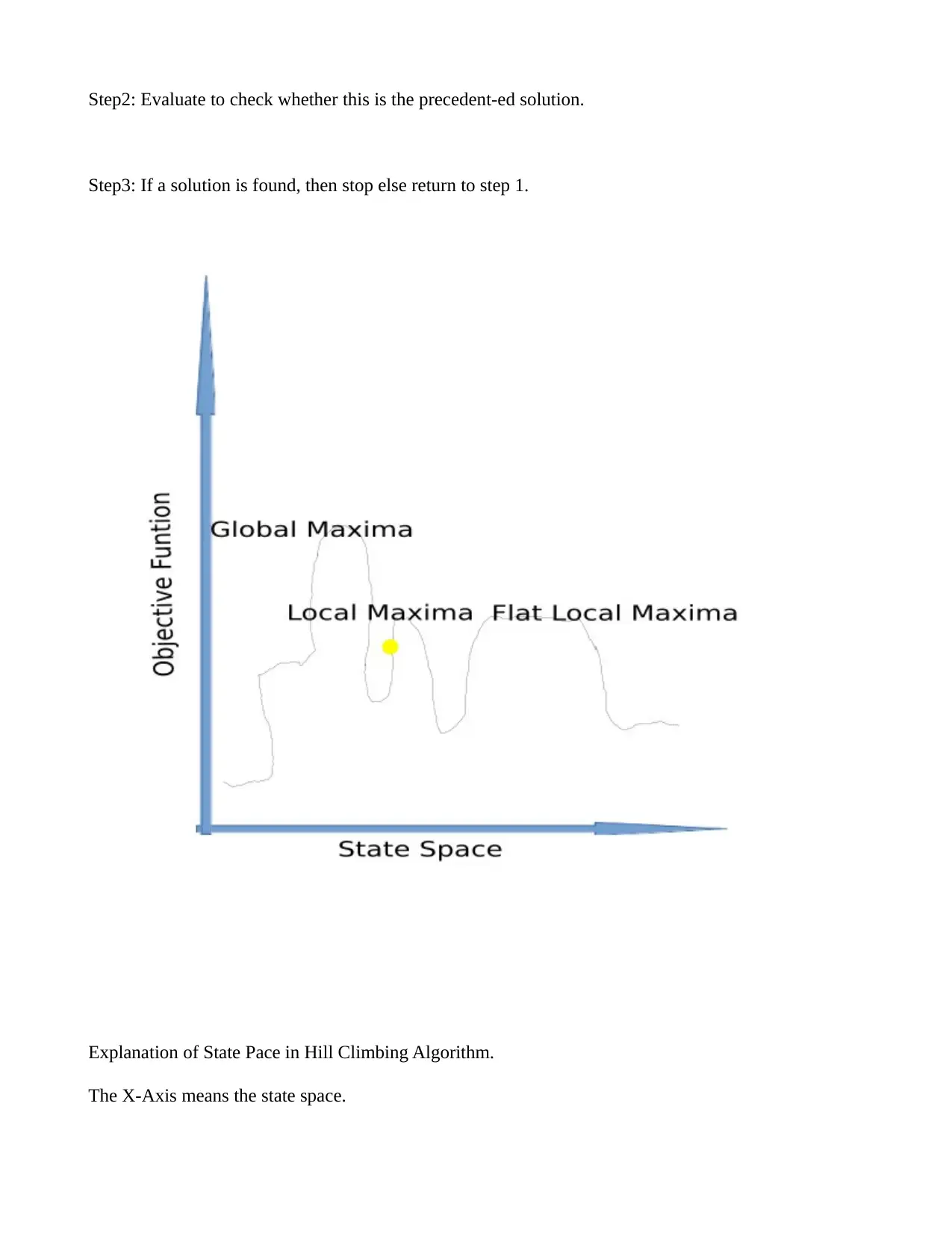
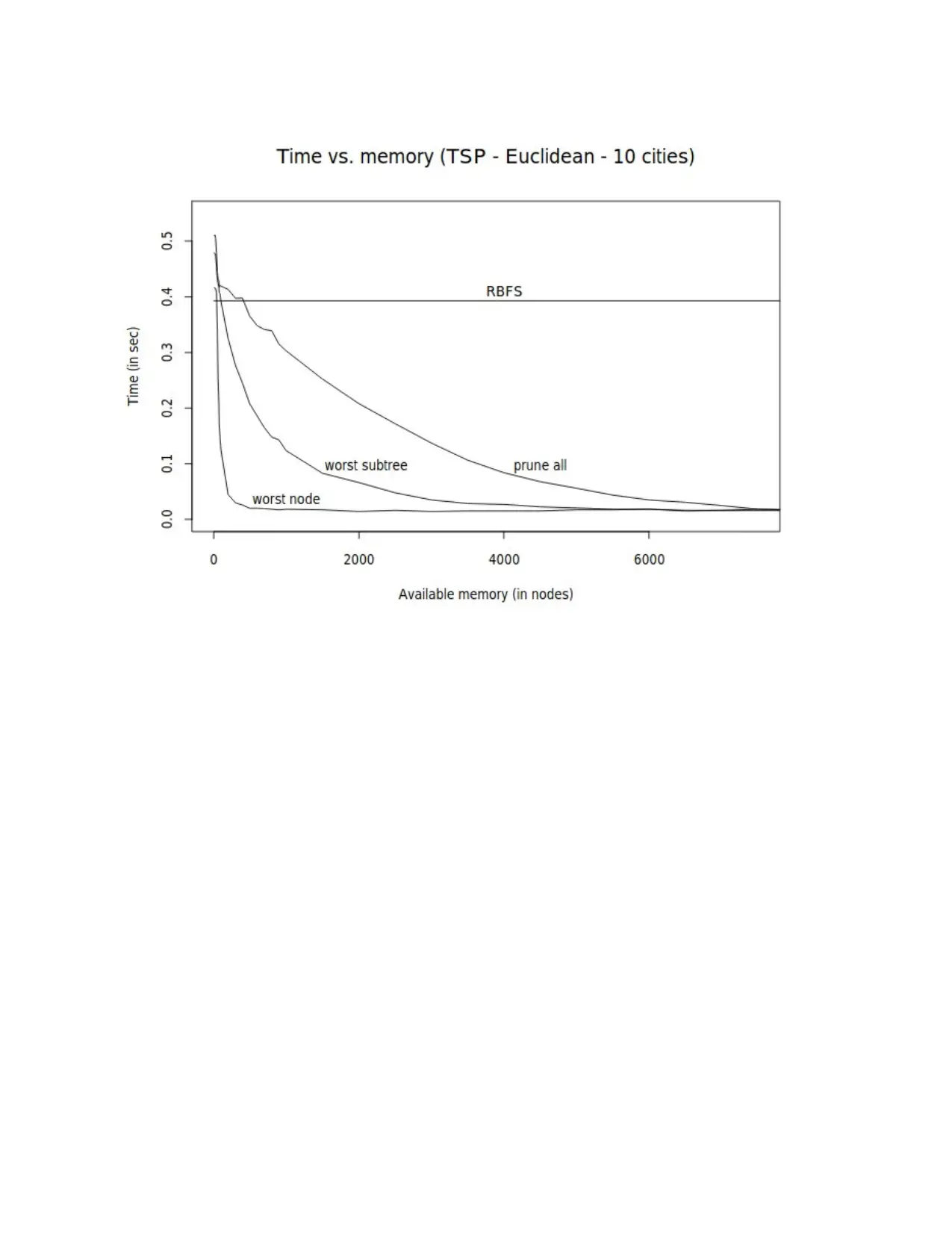
This assignment provides a detailed exploration of three core search algorithms in Artificial Intelligence: A*, Hill Climbing, and Recursive Best-First Search (RBFS). The solution begins with pseudo-code implementations of each algorithm, outlining their functionalities, including the initial state, goal state, successor functions, edge costs, and heuristic functions. The A* algorithm utilizes a combination of g(n) and h(n) to find the optimal path. The Hill Climbing algorithm, a heuristic search method, is explained with its pseudo-code and state space analysis, including local maxima, global maxima, and flat local maxima. The RBFS algorithm is also presented with its pseudo-code, along with an example demonstrating the relationship between search time and available memory. The assignment further includes Java source code implementations for the Hill Climbing algorithm applied to the Traveling Salesman Problem (TSP) and the RBFS algorithm. The code includes methods for generating distance matrices, swapping tour elements, and finding the best tour. Finally, the solution provides a comparison of the three algorithms, discussing their strengths, weaknesses, and suitability for different problem scenarios, highlighting the time and space trade-offs involved.

Programming Assignment
Institution
Date
Name

1.
a)
A* Algorithm
Initial State: The sales agent in the start city and hasn’t visited any city
Goal State: sales agent has made a visit to all cities and arrived at the beginning city once more.
Successor Function: Come up with urban communities that haven’t been visited
Edge-cost: Displacement among urban communities by the nodes, utilize this expense to calculate
g(n).
h(n): displacement to the closest unvisited city from the present city + evaluated displacement to travel
all the cities not visited (the MST heuristic is utilized here) + closest way from an unvisited city to the
start city.
Pseudo-code
function A*(start, goal)
setClosed := {}
setOpen := {start}
prevNode := an empty map
costScore := map with default value of Infinity
costScore[start] := 0
infinityScore := map with default value of Infinity
infinityScore[start] := heuristic_cost_estimate(start, goal)
while setOpen is not empty
curr := the node in setOpen having the lowest infinityScore[] value

if curr = goal
return reconstruct_path(prevNode, curr)
setOpen.Remove(curr)
setClosed.Add(curr)
for each the_neighbour of curr
if the_neighbour in setClosed
continue
if the_neighbour not in setOpen
setOpen.Add(the_neighbour)
gscoreTentative := costScore[curr] + dist_between(curr, the_neighbour)
if gscoreTentative >= costScore[the_neighbour]
continue
prevNode[the_neighbour] := curr
costScore[the_neighbour] := gscoreTentative
infinityScore[the_neighbour] := costScore[the_neighbour] +
heuristic_cost_estimate(the_neighbour, goal)
return failure
function reconstruct_path(prevNode, curr)
total_path := [curr]
while curr in prevNode.Keys:
curr := prevNode[curr]
total_path.append(curr)
return total_path

b) Hill Climbing
Pseudo-code.
k = initial solution
While f(s)<=f(k) s E Neighbors (k)
do
Generate an s E Neighbors(k);
IF fit(k) > fit(k) then
Replace s with k;
END IF
Hill Climbing is a heuristic search that is utilized for scientific streamlining issues in the field of
Artificial Intelligence.
Along these lines, given an enormous arrangement of data sources and a decent heuristic capacity, the
algorithm attempts to locate the most ideal answer for the issue in the most sensible timeframe. The
solution may not be the outright best(global ideal most extreme) however it is adequately acceptable
considering the time assigned (Bykov & Petrovic, 2016).
For this reason, the Hill climbing algorithm tackles the issues where we have to expand or limit a given
genuine capacity by choosing esteems from the given data sources.
The Algorithm Steps:
Step1: Come up with potential solutions.

Step2: Evaluate to check whether this is the precedent-ed solution.
Step3: If a solution is found, then stop else return to step 1.
Explanation of State Pace in Hill Climbing Algorithm.
The X-Axis means the state space.

The Y-Axis means the estimates the values of the objective function on a given state
Local maxima: Is a state that is superior to its neighboring state but there exists a state which is
superior to it (global extreme). This state is better in light of the fact that here the estimation of the
target work is higher than its neighbors.
Global maxima: It is the most ideal state in the state space graph. This in light of the fact that at this
state, the objective function is at its greatest value.
Flat local maxima: It is a level area of state space where neighboring states are of equal value.
Current state: The area of state space outline where we are at present during the inquiry. (Indicated by
the featured circle in the Illustration)
c).
Recursive Best-First Algorithm
Pseudocode
functionRFBS( problem, node, f_limit)
return a solution or failure and a new f-costlimit
if GOAL-TEST[problem](STATE[node]) then return node
successors ←EXPAND(node problem)

if successors is empty then return failure, ∞
for each s in successors do
f [s] ←max(g(s)+ h(s), f [node])
repeat
best←the lowest f-value node in successors
if f [best]> f_limitthen returnfailure, f [best]
alternative←the second lowest f-value among successors
result, f [best] ←RBFS(problem, best,min(f_limit, alternative))
if result≠failure then return result
Recursive Best-First Algorithm is a heuristic pursuit algorithm that grows fronteir nodes in the order of
best-first. It utilizes the issue explicit data about the enviroment to decide the inclination of one node
over the other. RBFS is like a recursive usage of profundity first inquiry, with the difference that it
utilizes an extraordinary condition for backtracking that guarantees that hubs are extended in best-first
order (Marinescu, Kishimoto et al., 2019). It works by maintaining on the recursion stack the full way
to the present hub being extended, just as every immediate children of nodes on that way, alongside
cost of the best node in the subtree investigated underneath every child. At whatever point the expense
of the node surpasses that of some other node in the recently extended bit of the tree, the algorithm will
back up to its deepest common ancestor, and proceeds the search down the nodes again.
Example: Relations between the search time and the available memory for the TSP with 10 cities using
the RBFA.

2. The Source Code
Hill Climbing.
import java.util.*;
public class TravelingSalesManProblem
{
public double[][] fillDistMatrix(int size, int seed)
{
double[][] distances=new double[size][size];
Random random=new Random(seed);
for(int i=0; i<size; i++)
for(int j=i+1; j<size; j++)
{
distances[i][j]=random.nextDouble();
distances[j][i]=distances[i][j];
}
return distances;
}
public double swap(int[] tour, int tourIndexA,
int tourIndexB, double[][] distances)
{

return 0;
}
public double getBestTour(int[] tour,
double[][] distances, int restarts,
int seed)
{
//must use random to create new randomly ordered tours
Random random=new Random(seed);
for(int i=0; i<restarts; i++)
{
randomTour(tour, random);
//put code here
}
return 0;
}
public void randomTour(int[] tour, Random random)
{
for(int i=0; i<tour.length; i++)
tour[i]=i;
//randomize the tour from here

}
/**test the TSP with various inputs
* @param argv
*/
public static void main(String[] argv)
{
int[] sizes={10, 20, 30, 40};
int[] seeds={1, 2, 3, 4};
int[] restarts={20, 20, 20, 20};
TravelingSalesManProblem sales=new TravelingSalesManProblem();
for(int i=0; i<sizes.length; i++)
{
double[][] distances=sales.fillDistMatrix(sizes[i], seeds[i]);
int[] tour=new int[sizes[i]];
double cost=sales.getBestTour(tour, distances, restarts[i], seeds[i]);
System.out.println("Cost Printed Out here "+cost);
for(int j=0; j<tour.length; j++)
System.out.print(tour[j]+" ");
System.out.println();
}
}
}