MAT-121: College Algebra - Written Assignment 4: Complete Solution

This document provides a comprehensive solution to the MAT-121 College Algebra Written Assignment 4. It covers a range of topics including rewriting quadratic functions in standard form, determining minimum/maximum values, finding the vertex and axis of symmetry, and determining domain and range. The solution also includes the application of these concepts to real-world problems, such as maximizing revenue in an athletic stadium scenario. Furthermore, the assignment delves into the identification of power and polynomial functions, finding intercepts, and graphing polynomial functions. It explores concepts like degree, leading coefficients, x-intercepts, and end behavior. The solution also covers polynomial division, synthetic division, the Remainder Theorem, the Factor Theorem, and the Rational Zero Theorem. Additionally, it addresses complex solutions, Descartes' Rule, and the construction of polynomial functions based on given information. The assignment concludes with finding the domain, intercepts, slant asymptotes, and sketching graphs of rational functions, as well as finding the inverse of a function. This detailed solution is designed to aid students in understanding and mastering the concepts of college algebra.

MAT-121: COLLEGE ALGEBRA
Written Assignment 4
2.5 points each
SECTION 5.1
Algebraic
For the following exercise, rewrite the quadratic function in standard form and give the vertex.
1. y=4 x2+5 x −7
For the following exercise, determine whether there is a minimum or maximum value to the
quadratic function. Find the value and the axis of symmetry.
For a function with minimum the x^2 coefficient is greater than zero and a function with
maximum the coefficient is less than zero. The coefficients can be expressed as
y = a x2 +bx+ c
so, a = 4, b = 5, and c = 7. Since a > 0, the function has a minimum.
To get the value at the symmetry, one need to find the first derivative of the function y and
equate it to zero.
y=4 x2+5 x −7
dy
dx =8 x+5 =0
x = −5
8
This is the line of symmetry and is along the x-axis.
2. y= 1
3 x2−4 x +9
For the following exercise, rewrite the quadratic function in standard form and give the vertex.
Determine whether there is a minimum or maximum value to the quadratic function. Find the
value and the axis of symmetry. Determine the domain and range of the quadratic function.
ANSWER
The standard form of equation is y = a ( x−h ) 2+ k, where (h, k) is the vertex of the quadratic
equation. We use completing square method to get the standard form of the equation.
3y = ( x2−12 x )+ 27
Copyright © 2019 by Thomas Edison State University. All rights reserved.

3y= ( x2−12 x+ ( 12
2 )
2
) +27−( 12
2 )
2
3y = ( x−6 )2+27−36
3y= ( x−6 )2−9
y = 1
3 ( x−6 )2−3
From the standard form the vertex of the equation is (6, -3).
3. f ( x)=−1
2 x2 +4 x−2
Answer
−2 y=x2−8 x +4
−2 y= ( x2−8 x ) + 4
−2 y= (x2−8 x+ ( 8
2 )2
)+4− ( 8
2 )2
−2 y= ( x−4 ) 2 + 4−16
y = −1
2 ( x−4 )2 +6
From the standard form the vertex of the equation is (4, 6).
For the following exercise, use the vertex (h, k) and a point on the graph (x, y) to find the general
form of the equation of the quadratic function.
4. (h , k )=(−1 ,3) ,
(x , y )=(−2 , 6)
Answer
The standard form of the equation is;
y = a ( x−h ) 2+ k
6 = a (−2− ( −1 ) ) 2 +3
6 = a ( −1 ) 2 +3
a = 3
Thus, the standard form of the quadratic equation is;
y = 3 ( x+1 )2+3
The general form is;
y = 3 ( x2+ 2 x +1 ) +3
y = 3 x2+ 6 x +6
Copyright © 2019 by Thomas Edison State University. All rights reserved.

Real-World Applications
5. An athletic stadium holds 105,000 fans. With a ticket price of $22, the average
attendance has been 32,000. When the price dropped to $16, the average attendance rose
to 50,000. Assuming that attendance is linearly related to ticket price, what ticket price
would maximize revenue? Round ticket price to the nearest ten cents.
Answer
The points of the line are (22, 32000) and (16, 50000)
Gradient = m = 50000−32000
16−22 = -3000
A = −3000 t+ b
When ticket cost $16 the attendance is 50,000.
50,000 = -3,000 (16) + b
b = 98,000
The linear equation is
Q = -3000t + 98,000
The total revenue will be
= Price∗Quantity
= −3000 t2 + 98000t
The marginal revenue will be
= d
dt (total revenue)
= d
dt (−3,000 t2+ 98,000 t)
= −6,000 t +98,000
The total revenue will be maximized when the marginal revenue is equal to zero.
-6,000t + 98,000 = 0
t = 98,000
6,000
t = 16.33
Thus, the ticket price should be at $16.33 to maximize revenue.
SECTION 5.2
Algebraic
For the following exercise, identify the function as a power function, a polynomial function, or
neither.
Copyright © 2019 by Thomas Edison State University. All rights reserved.

6. f ( x)=4 ( x3 )
3
Answer
This can be expressed as
f ( x ) = 4 x9
Power function can be expressed as; y = k x p; where k and p are real numbers. Thus, the
function f ( x )is as power function.
For the following exercise, find the degree and leading coefficient for the given function if it is a
polynomial. If it is not a polynomial, then state so.
7. f ( x)= ( 2 x2−5 )2
+ ( x−3 )2 +5
Answer
We write the function in a general form;
f ( x ) = 4 x4−20 x2+ 25+ ( x−3 ) 2 +5
= 4 x4−20 x2+ 25+ x2−6 x+ 9+5
= 4 x4−19 x2−6 x +39
The leading coefficient is; 4 and is of degree 4.
For the following exercise, find the intercepts of the functions.
8. g( x )= ( 3 x2−10 x−8 ) ( x +3 )
Answer
Expanding the function, we have;
g ( x ) = 3 x3−x2−38 x−24
The y-intercept is (0, -24)
This will have three x-intercepts, when g ( x ) = 0;
3 x3−x2−38 x−24=0
By factorization;
( 3 x2−10 x−8 ) ( x +3 )=0
( 3 x+2 ) ( x−4 ) ( x +3 ) =0; x = −2
3 , x= 4, x = -3
The intercepts are at the point (−2
3 , 0 ), ( 4 , 0 )∧ (−3 , 0 )
Technology
For the following exercise, graph the polynomial function using a calculator or a graphing utility.
Based on the graph, determine the intercepts and the end behavior.
Copyright © 2019 by Thomas Edison State University. All rights reserved.

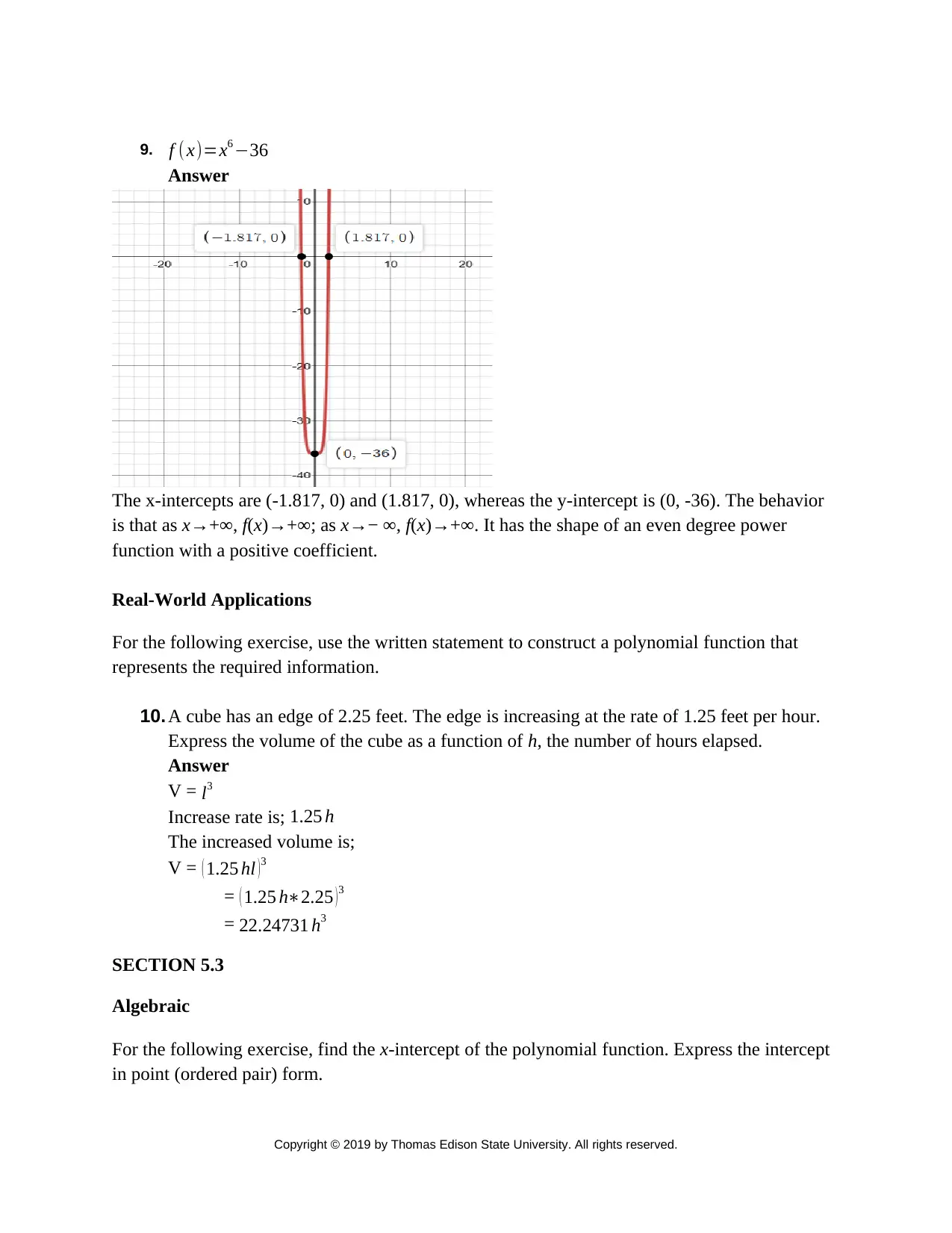
9. f ( x)=x6 −36
Answer
The x-intercepts are (-1.817, 0) and (1.817, 0), whereas the y-intercept is (0, -36). The behavior
is that as x→+∞, f(x)→+∞; as x→− ∞, f(x)→+∞. It has the shape of an even degree power
function with a positive coefficient.
Real-World Applications
For the following exercise, use the written statement to construct a polynomial function that
represents the required information.
10. A cube has an edge of 2.25 feet. The edge is increasing at the rate of 1.25 feet per hour.
Express the volume of the cube as a function of h, the number of hours elapsed.
Answer
V = l3
Increase rate is; 1.25 h
The increased volume is;
V = ( 1.25 hl ) 3
= ( 1.25 h∗2.25 ) 3
= 22.24731 h3
SECTION 5.3
Algebraic
For the following exercise, find the x-intercept of the polynomial function. Express the intercept
in point (ordered pair) form.
Copyright © 2019 by Thomas Edison State University. All rights reserved.

11. f ( x)=5 x3−20 x2 +2 x −8
Answer
Factoring we have;
( x−4 ) ( 5 x2+2 ) =0
x = 4; x = √ −2
5 , which absurd. Thus, this function has one intercept. The x-intercept is
(4, 0)
For the following exercise, use the Intermediate Value Theorem to confirm that the given
polynomial has at least one zero within the given interval.
12. g( x )=−3 x3−12 x2 +11 x between x = -5 and x = -4
Answer
At x = -5
g ( x )=−3 (−5 )3−12 (−5 )2 +11(−5)
g ( x ) = 20
at this point the curve is above zero
At x = -4
g ( x ) =−3 ( −4 ) 3−12 ( −4 ) 2 +11(−4)
g ( x ) = -44
at this point, the curve is above zero.
Therefore, there is a solution between the interval [-5, -4].
Graphical
For the following exercise, graph the polynomial function. Note x- and y-intercepts, multiplicity,
and end behavior.
13. f ( x)=x(x +4)(x−4)(x+ 7)
For the following exercises, use the given information about the polynomial graph to write the
equation.
Answer
Copyright © 2019 by Thomas Edison State University. All rights reserved.

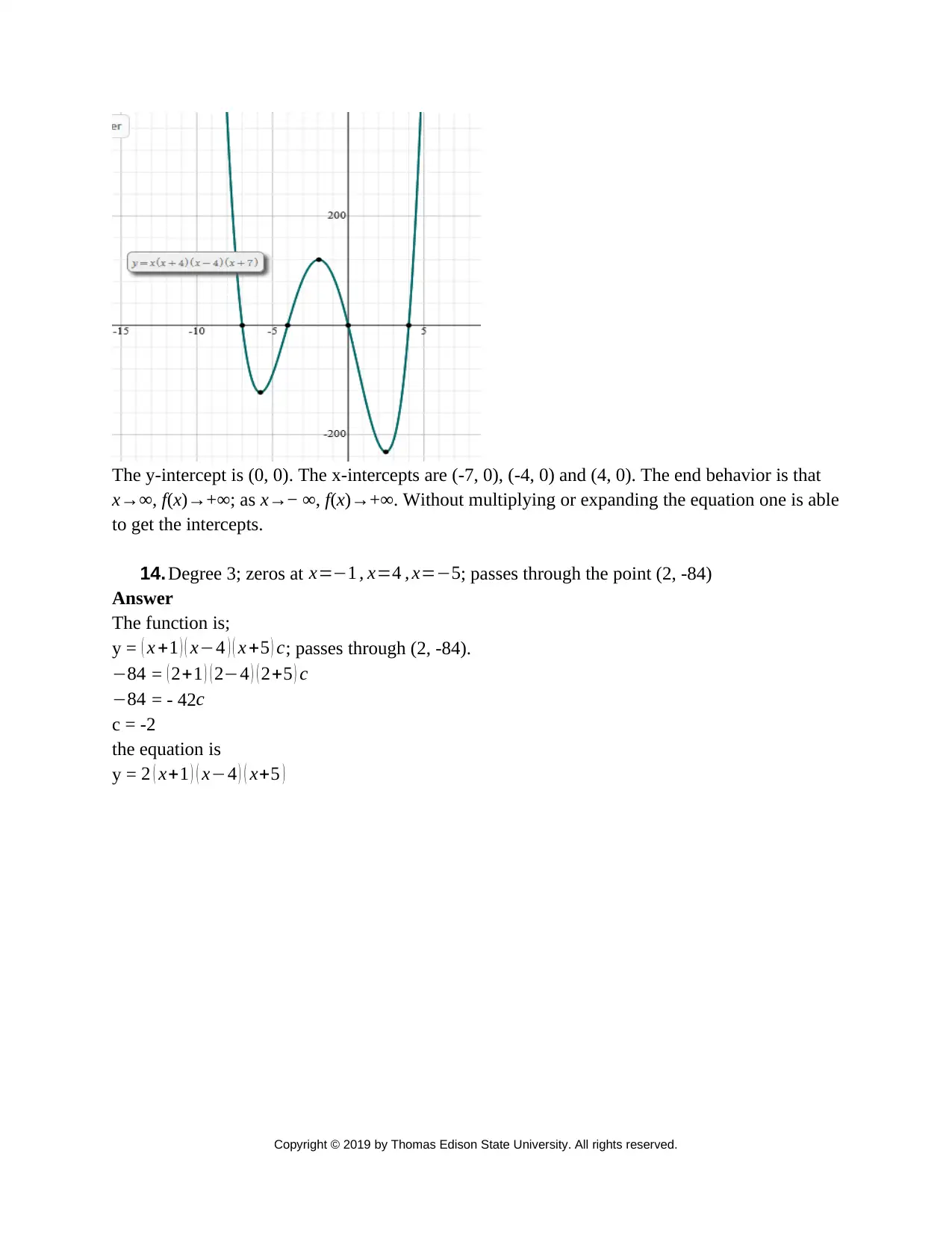
The y-intercept is (0, 0). The x-intercepts are (-7, 0), (-4, 0) and (4, 0). The end behavior is that
x→∞, f(x)→+∞; as x→− ∞, f(x)→+∞. Without multiplying or expanding the equation one is able
to get the intercepts.
14. Degree 3; zeros at x=−1 , x=4 , x=−5; passes through the point (2, -84)
Answer
The function is;
y = ( x +1 ) ( x−4 ) ( x +5 ) c; passes through (2, -84).
−84 = ( 2+1 ) ( 2−4 ) ( 2+5 ) c
−84 = - 42c
c = -2
the equation is
y = 2 ( x+1 ) ( x−4 ) ( x+5 )
Copyright © 2019 by Thomas Edison State University. All rights reserved.

The y-intercept is (40, 0). The x-intercepts are (-5, 0), (-1, 0) and (4, 0). The end behavior is that
x→ +∞, f(x)→+∞; as x→− ∞, f(x)→ -∞.
Real-World Applications
15. A cylinder has a radius of 2 x+3units and a height of 5 units greater than the radius.
Express the volume of the cylinder as a polynomial function.
Answer
V = π r2 h; r = 2x + 3, h = 2x + 3 +5 = 2x + 8
= π ( 2 x +3 )2 ( 2 x +8 )
= π ( 2 x ( 2 x +3 )2 +8 ( 2 x+ 3 ) 2 )
= π ( 2 x ( 4 x2 +12 x+ 9 ) +8 ( 4 x2+12 x +9 ) )
V = π ( 8 x3 +56 x2 +114 x+ 72 )
Which is the required polynomial function.
SECTION 5.4
For the following exercises, use long division to divide. Specify the quotient and the remainder.
16. ( x2−6 x +4 ) ÷ ( x −2 )
Answer
Copyright © 2019 by Thomas Edison State University. All rights reserved.

x −4
x−2 x2−6 x +4
−¿ x2−2 x
Drop 4 −4 x −4 x+ 4
−¿ −4 x+ 4
0
Thus, the quotient is x−4, with no remainder.
For the following exercises, use synthetic division to find the quotient.
17. ( 18 x3+ 3 x2−33 x +20 ) ÷ ( 3 x +5 )
Power 3 2 1 0
5
3
18 3 -33 20
↓ 30 45 -20
18 -27 12 0
The remainder is zero.
The quotient is; 18 x2−27 x+12
For the following exercises, use synthetic division to determine whether the first expression is a
factor of the second. If it is, indicate the factorization.
18. x−3 ; 2 x2 +7 x−12
Power 2 1 0
3 2 7 -12
↓ 6 39
2 13 27
The remainder is 27
Y = 2 x+13+ 27
x−3 ; this is an indication that the expression x−3 is not factor of 2 x2 +7 x−12.
For the following exercises, use synthetic division to find the quotient and remainder.
19. 2 x3−6 x2 +5
2 x +3
Copyright © 2019 by Thomas Edison State University. All rights reserved.

Power 3 2 1 0
−3
2
2 6 0 5
↓ -6 0 0
2 0 0 5
The quotient is 2 x2 and the remainder is 5.
Extensions
For the following exercises, use synthetic division to determine the quotient involving a complex
number.
20. x2 +3
x −i
Power 2 1 0
i 1 0 3
↓ i -1
1 i 2
The quotient is x +i and a remainder of 2.
Copyright © 2019 by Thomas Edison State University. All rights reserved.

SECTION 5.5
Algebraic
For the following exercises, use the Remainder Theorem to find the remainder which is the value
of f(x) at x = k. Then evaluate f(x) at x = k to verify remainder and f(x) at x = k are the same.
Show all work for both synthetic division and the evaluation of f(x) at x = k.
21. ( 2 x4−5 x3 +2 x2−x −1 ) ÷ ( 2 x+1 )
Power 4 3 2 1 0
−1
2
2 -5 2 -1 -1
↓ -1 3 -2.5 1.75
2 -6 5 -3.5 0.75
f (x=k )=r
= 2 (−0.5 )4 −5 (−0.5 )3 +2 (−0.5 )2− (−0.5 )−1
= 0.75, which verifies that the remainder is correct.
For the following exercises, use the Factor Theorem to find all real zeros for the given
polynomial function and one factor.
22. f ( x)=6 x3 −13 x2−73 x−60 ; 2 x+ 3
Power 3 2 1 0
−3
2
6 -13 -73 -60
-9 33 60
6 -22 -40 0
The remainder is zero, which shows that 2x + 3 is a factor.
6 x3 −13 x2−73 x−60
2 x +3 = 6 x2−22 x−40 = 2 ( 3 x2 −11 x−20 ) = 2 ( 3 x + 4 ) ( x−5 )
Thus, the 2 ( 3 x + 4 ) ( x−5 ) ( 2 x +3 ), the real zeros are x = −4
3 , x = 5, x = −3
2 .
Copyright © 2019 by Thomas Edison State University. All rights reserved.

For the following exercises, use the Rational Zero Theorem to find all real zeros. State all the
possible rational zeros.
23. 4 x3 −7 x−3=0
The possible real zeros are;
3 =: 1, 3
4 =: 1, 2, 4
All possible rational real zeros {1, 1
2, 1
4 , 3, 3
2, 3
4 }
Taking the simplest possible real zero;
4 (1)3−7∗1−3=¿ 0
Thus, ( x−1 ) is a factor.
Taking -1,
4 ¿(−1)3−7∗−1−3=¿ 0
Thus, ( x +1 ) is a factor.
Taking 1
3;
4 ¿ ( −1
2 )
3
− 7∗−1
2 −3=¿ −22
27
4 ¿ ( 3 ) 3−7∗3−3 = 84
(x− 1
3 ) and (x + 1
3 ) are not a factor.
4 ¿ ( 3
2 )
3
−7∗3
2 −3 = 0
Thus, (x− 3
2 ) is the third root.
For the following exercises, find all complex solutions (real and non-real).
24. 4 x3 −8 x2+ 9 x−18=0
The possible solution is;
18 =: 1, 2, 3, 6, 9, 18
4 =: 1, 2, 4
Possible solution = {1, 1
2 , 1
4 , 2, 3 , 3
2 , 3
4 ,6 , 9 , 9
2 , 9
4 , 18 }
4 ( 1 ) 3−8 ( 1 ) 2 +9 ( 1 ) −18=¿ −13
4 ( 2 ) 3−8 ( 2 ) 2 +9 ( 2 ) −18 = 0
Thus, ( x−2 ) is a factor; all others are not equal to zero. Thus, this function has only one
root at x = 2
Copyright © 2019 by Thomas Edison State University. All rights reserved.

Graphical
Use Descartes’ Rule to determine the possible number of positive and negative solutions. Make a
table of possible real/complex solutions as shown in example 8 of Section 5.5. Then graph to
confirm which of those possibilities is the actual combination.
25. f (x)=x4−2 x3−3 x2 +5 x−3
Possible positive zeros;
Three positives, or one possible positive
Possible negative zeros
f (x)= ( −x ) 4−2 ( −x ) 3−3 ( −x ) 2+ 5 ( −x ) −3
f ( x )=x4 + 2 x3−3 x2−5 x−3
One possible negative
factors
3 1, 3
1 1
1, 3 Solution
x = ±1 or x = ± 3
The plot shows that none of the solution given possible solution is correct.
Copyright © 2019 by Thomas Edison State University. All rights reserved.

Technology
For the following exercises, use your graphing calculator or a graphing utility program to graph
the polynomial function. Based on the graph, find the rational zeros. All real solutions are
rational.
26. f ( x)=12 x4 −11 x3 +33 x2 −44 x−60
The rational zeros are; x = −3
4 , and x = 5
3
Extensions
For the following exercises, construct a polynomial function of least degree possible using the
given information.
27. Real roots: −2, 2, -3 and f (3)=10
The equation is in the form of;
y = a ( x +2 ) ( x −2 ) ( x +3 )
10 = a ( 3+2 ) ( 3−2 ) ( 3+3 )
a = 1
3
The general polynomial is;
y = 1
3 ( x +2 ) ( x−2 ) ( x +3 )
Copyright © 2019 by Thomas Edison State University. All rights reserved.

y = 1
3 ( x2−4 ) ( x +3 )
= 1
3 ( x3 +3 x2 −4 x−12 )
= x
3
3
+x2− 4
3 x−4, which is the required polynomial.
Real-World Applications
For the following exercises, find the dimensions of the right circular cylinder described.
28. The radius is half height. The volume is128 π cubic feet.
SECTION 5.6
Algebraic
For the following exercises, find the domain of the rational functions.
29. f ( x)= 2 x2 +5 x−12
4 x2+13 x−35
4 x2 +13 x−35=0
x = −13 ± √ ( 132−4∗4∗−35 )
2∗4
x = 7
4 , x = −¿5
f ( x ) is undefined at these points. Thus, the domain is;
x ←5; −5< x < 7
4 ; x > 7
4
or(−∞,−5 ) ∪ (−5 , 7
4 )∪ ( 7
4 , ∞ )
For the following exercises, find the x- and y-intercepts for the functions.
30. f ( x)=3 x2−4 x−8
8 x3 +64
Copyright © 2019 by Thomas Edison State University. All rights reserved.

3 x2−4 x−8
8 x3+64 =0
3 x2−4 x −8=0
x = −(−4) ± √ ( ( −4 ) 2−4∗3∗−8 )
2∗3
x = 2 ( 1+ √7 )
3 , x = 2 ( 1− √ 7 )
3
The y-intercept is when x = 0
f ( x)=3 ( 0 )2 −4 ( 0 )−8
8 ( 0 )3+ 64 = −8
64 =−1
8
For the following exercises, find the slant asymptote of the functions.
31. f ( x)=3 x3+4 x2−7 x +12
x2 +3
If numerator's degree =1 + denominator's degree, the asymptote is a slant asymptote of
the form: y=mx+b .
This can be expressed in form of quotient and remainder as follows;
3 x+ 4+ ( −16 x
x2+3 ), this shows that the slant asymptote is 3 x+ 4.
For the following exercises, find the horizontal intercepts, the vertical intercept, the vertical
asymptotes, and the horizontal or slant asymptote of the functions. Use that information to sketch
a graph.
32. f ( x)= 3 x2−7 x−20
x3−2 x2−29 x−42
If denominator's degree > numerator's degree, the horizontal asymptote is the x-axis: y=0.
For the following exercises, write an equation for a rational function with the given
characteristics.
33. Vertical asymptotes atx=−7∧x= 3
2 , x-intercepts at (−6,0 )∧ ( 3,0 ), y-intercept at (0 , 6
7 ),
horizontal asymptote at y= 1
2
Copyright © 2019 by Thomas Edison State University. All rights reserved.

f ( x ) =
a ( x+ 6 ) ( x −3 )
( x +7 ) (x− 3
2 )
the horizontal asymptote shows that powers are equal. We use the y-intercept to get the
value of a.
6
7 =
a ( 0+6 ) ( 0−3 )
( 0+7 ) (0− 3
2 )
a = 0.5, this coincide with the horizontal asymptote. Thus, the equation is;
f ( x ) =
( x+6 ) ( x−3 )
2 ( x +7 ) ( x−3
2 )
SECTION 5.7
Algebraic
For the following exercises, find the inverse of the function on the given domain.
34. f ( x)= ( x+6 ) 2 , ¿
If a function f(x) is mapping x to y, then the inverse function of f(x) maps y back to x.
y = ( x +6 )2 → x= ( y +6 )2 and we solve for y.
y + 6 = ± √x
y = ± √ x −6
this means that y = √ x−6 or y = − √ x−6
in both cases, x≥ 0, but only y = √ x−6 is on the domain , ¿.
For the following exercises, find the inverse of the functions.
35. f (x)=4 x3 +5
If a function f(x) is mapping x to y, then the inverse function of f(x) maps y back to x.
y = 4 x3 +5 → x=4 y3 +5 and we solve for y.
x=4 y3 +5
4 y3 = x−5
y = 3
√ x−5
4 = ( x−5
4 ) 1
3
Copyright © 2019 by Thomas Edison State University. All rights reserved.

For the following exercises, find the inverse of the functions.
36. f ( x)= √ 3 x +4
x = √3 y+4
x2 = 3y + 4
y= x2
3 − 4
3 , which is the inverse of the function.
Graphical
For the following exercises, find the inverse of the function and graph both the function and its
inverse.
37. f ( x)=3 x2 +5 , x ≥ 0
y = 3 x3+5 → x=3 y3 +5 and we solve for y.
x=3 y3 +5
3 y3 = x−5
y = 3
√ x−5
3 = ( x−5
3 )1
3
SECTION 5.8
Algebraic
For the following exercises, write an equation describing the relationship of the given variables.
38. y varies directly with the cube of x and inversely with the square of z, when
x=4∧z=2 , y =8
Copyright © 2019 by Thomas Edison State University. All rights reserved.

Answer
y∝ x3 and y ∝ 1
z2
y=k x3 > 8 = k ( 4 ) 3
k =0.125
y = 0.125 x3
y= c
z2 > 8 = c
22
c=32
y = 32
z2
Numeric
For the following exercises, write an equation describing the relationship of the given variables.
Then use the given information to find the unknown value.
39. y varies jointly with the fourth root of a and the square of b and inversely with the cube
of c, when a=81∧b=7∧c=3 , y=49.
Answer
y ∝ a
1
4 b2
c3
y ¿ K a
1
4 b2
c3
49 = K 81
1
4∗72
33
K=9
y ¿ 9 a
1
4 b2
c3
Real-World Applications
For the following exercises, use the given information to answer the questions.
40. A person’s body mass index (BMI) b varies directly to a person’s weight in pounds and
inversely with the square person’s height h in inches. If a 6 foot tall person’s BMI is 32
Copyright © 2019 by Thomas Edison State University. All rights reserved.

and their weight is 236 pounds, write an equation describing the relationship of the given
variables. NOTE: Keep k as an exact fractional value not a decimal approximation.
Answer
b ∝ w
h2
b=k w
h2
32=k 236
62
k = 288
59
The relationship is;
b= 288 w
59 h2
Copyright © 2019 by Thomas Edison State University. All rights reserved.