MATH130: Algebra Assignment 2 Solution - [University Name] - May 2019
VerifiedAdded on 2023/03/31
|11
|1016
|411
Homework Assignment
AI Summary
This document presents a complete solution to an Algebra assignment (MATH130), addressing various mathematical concepts. The solution begins with an analysis of exponential decay, modeling the decrease of medicine in a patient's bloodstream. It then delves into trigonometric functions, specifically focusing on the cosine function and its properties within different quadrants. Furthermore, the assignment explores function analysis, including finding roots, sketching graphs, and interpreting function behavior. Additionally, the solution calculates marginal revenue using calculus, demonstrating how to determine the additional revenue generated by selling a unit of goods. Finally, the assignment covers basic calculus concepts, including integration and rate of change.

Running head: ALGEBRA 1
Algebra
Name
Institution
Algebra
Name
Institution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

ALGEBRA 2
Algebra
Question 1
Part a
Q=f ( t )=300 ( 0.75 )
t
40 = A × e−kt
Taking the natural log on both sides of the equation yields:
ln ( Q ) =ln ( 300 ) +ln ( ( 0.75 )
t
40 ) =5.7038+ t
40 ln (0.75)
¿ 5.7038+ t
40 ln (0.75)
ln ( Q )=5.7038− t
40 × 0.28768=5.7038−0.007192 t
Q=e5.7038 × e−0.007192 t =300 e−0.007192t
Therefore , A=300∧k =0.007192
Part b
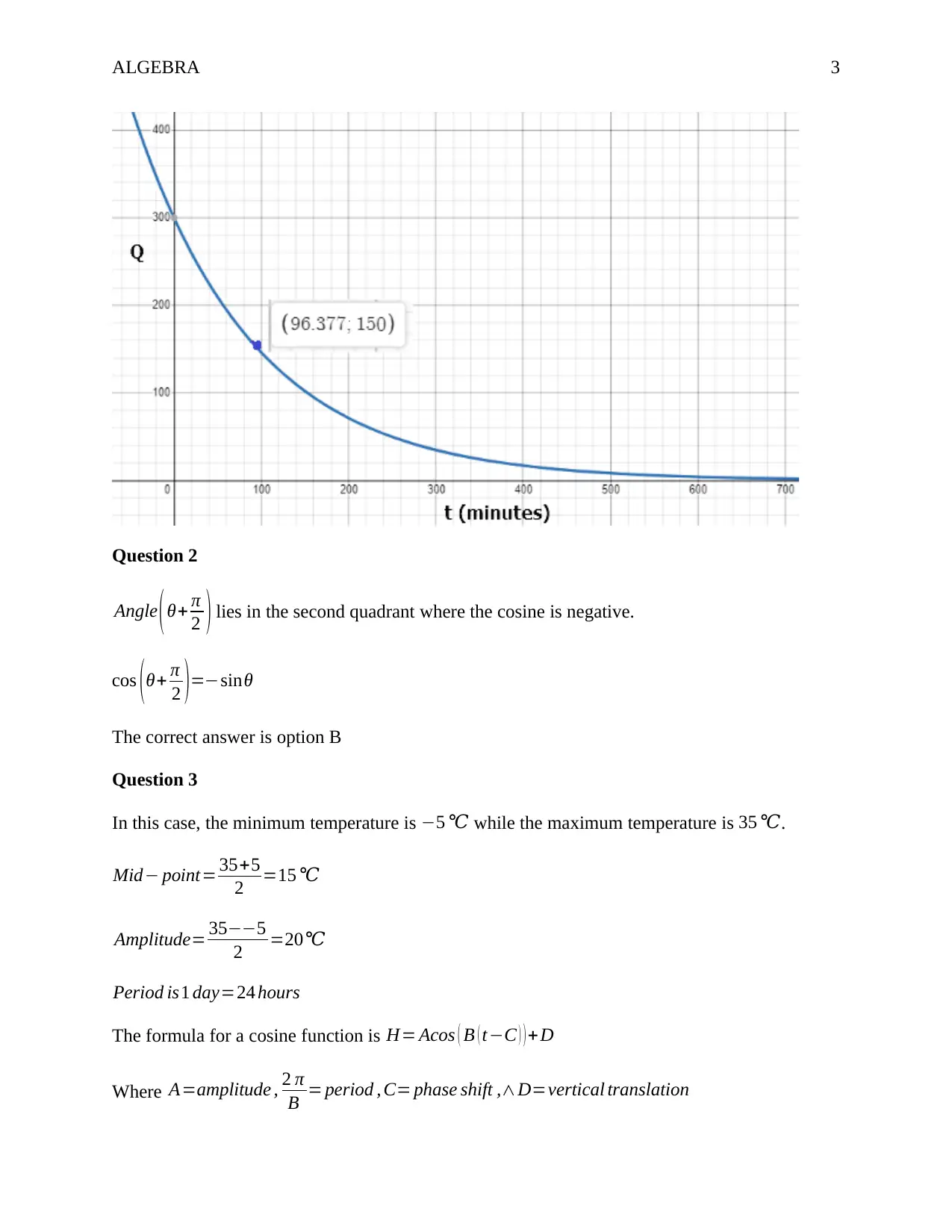
Initial quantity when t=0 is 300mg
Half the quantity=150mg
Q=300 ( 0.75 )
t
40 =150
( 0.75 )
t
40 =150
300 =0.5
ln ( 0.75 )
t
40 =ln (0.5)
t
40 ln ( 0.75 ) =ln (0.5)
t= 40 ln (0.5)
ln ( 0.75 ) =96.3768 minutes
Part c
Algebra
Question 1
Part a
Q=f ( t )=300 ( 0.75 )
t
40 = A × e−kt
Taking the natural log on both sides of the equation yields:
ln ( Q ) =ln ( 300 ) +ln ( ( 0.75 )
t
40 ) =5.7038+ t
40 ln (0.75)
¿ 5.7038+ t
40 ln (0.75)
ln ( Q )=5.7038− t
40 × 0.28768=5.7038−0.007192 t
Q=e5.7038 × e−0.007192 t =300 e−0.007192t
Therefore , A=300∧k =0.007192
Part b
Initial quantity when t=0 is 300mg
Half the quantity=150mg
Q=300 ( 0.75 )
t
40 =150
( 0.75 )
t
40 =150
300 =0.5
ln ( 0.75 )
t
40 =ln (0.5)
t
40 ln ( 0.75 ) =ln (0.5)
t= 40 ln (0.5)
ln ( 0.75 ) =96.3768 minutes
Part c
ALGEBRA 3
Question 2
Angle (θ+ π
2 ) lies in the second quadrant where the cosine is negative.
cos ( θ+ π
2 )=−sinθ
The correct answer is option B
Question 3
In this case, the minimum temperature is −5 ℃ while the maximum temperature is 35 ℃.
Mid− point= 35+5
2 =15 ℃
Amplitude= 35−−5
2 =20℃
Period is1 day=24 hours
The formula for a cosine function is H= Acos ( B ( t−C ) ) +D
Where A=amplitude , 2 π
B = period , C= phase shift ,∧D=vertical translation
Question 2
Angle (θ+ π
2 ) lies in the second quadrant where the cosine is negative.
cos ( θ+ π
2 )=−sinθ
The correct answer is option B
Question 3
In this case, the minimum temperature is −5 ℃ while the maximum temperature is 35 ℃.
Mid− point= 35+5
2 =15 ℃
Amplitude= 35−−5
2 =20℃
Period is1 day=24 hours
The formula for a cosine function is H= Acos ( B ( t−C ) ) +D
Where A=amplitude , 2 π
B = period , C= phase shift ,∧D=vertical translation
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
ALGEBRA 4
2 π
B =24 , B= π
12
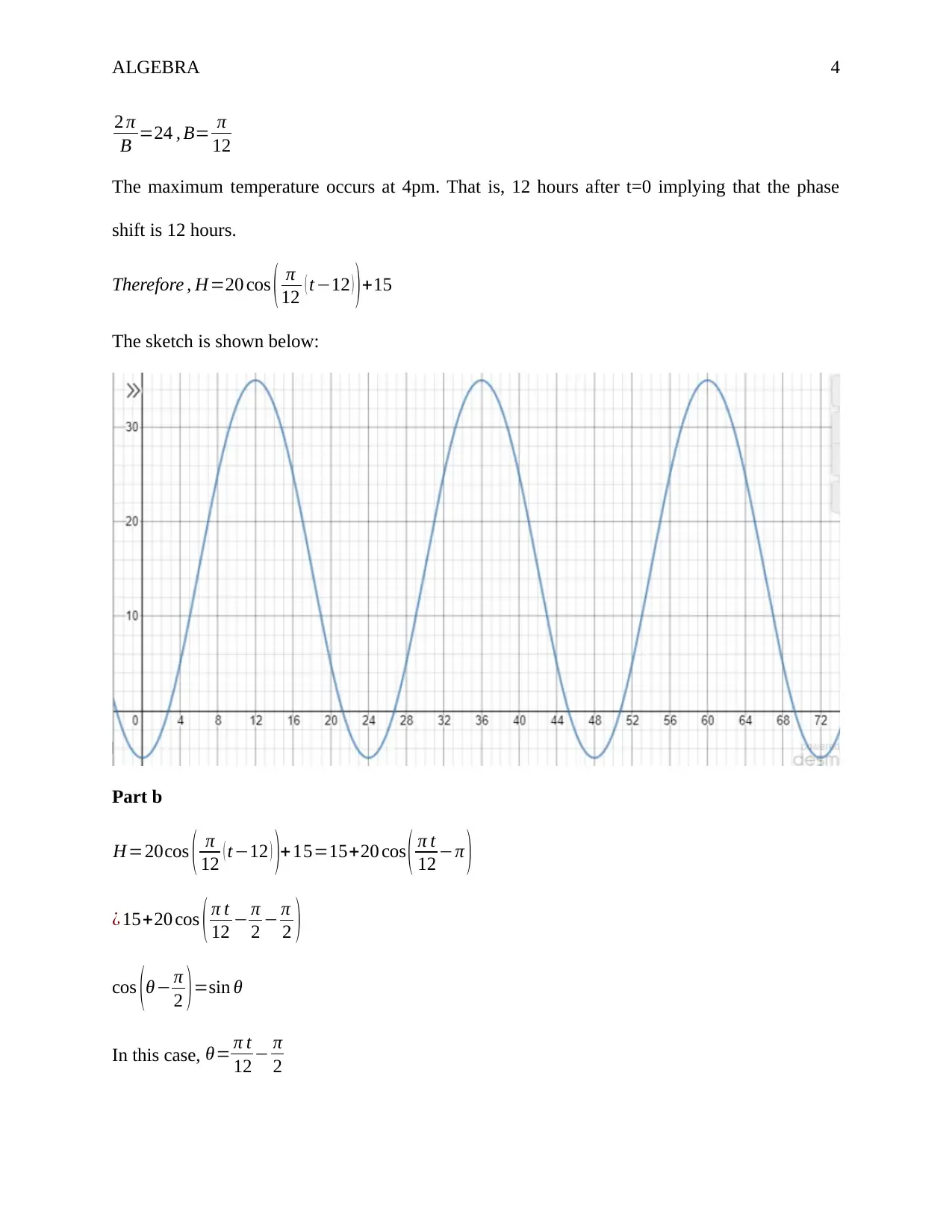
The maximum temperature occurs at 4pm. That is, 12 hours after t=0 implying that the phase
shift is 12 hours.
Therefore , H=20 cos ( π
12 ( t−12 ) ) +15
The sketch is shown below:
Part b
H=20cos ( π
12 ( t−12 ) )+15=15+20 cos ( π t
12 −π )
¿ 15+20 cos ( π t
12 − π
2 − π
2 )
cos (θ− π
2 )=sin θ
In this case, θ= π t
12 − π
2
2 π
B =24 , B= π
12
The maximum temperature occurs at 4pm. That is, 12 hours after t=0 implying that the phase
shift is 12 hours.
Therefore , H=20 cos ( π
12 ( t−12 ) ) +15
The sketch is shown below:
Part b
H=20cos ( π
12 ( t−12 ) )+15=15+20 cos ( π t
12 −π )
¿ 15+20 cos ( π t
12 − π
2 − π
2 )
cos (θ− π
2 )=sin θ
In this case, θ= π t
12 − π
2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

ALGEBRA 5
15+20 cos ( π t
12 − π
2 − π
2 )=15+sin ( πt
12 − π
2 )
H=15+sin ( πt
12 − π
2 )=A +B ¿
Therefore , A=15∧C= π
12
Question 4
f ( x )=2 x3−7 x +2
Part a
f ( 0 )=2(0)3−7 ( 0 ) +2=2
f ( 1 ) =2(1)3 −7 ( 1 )+ 2=2−7 +2=−3
f (−1 )=2(−1)3−7 (−1 ) +2=−2+ 7+2=7
f ( −2 ) =2(−2)3−7 ( −2 ) +2=−16+14+2=0
Part b
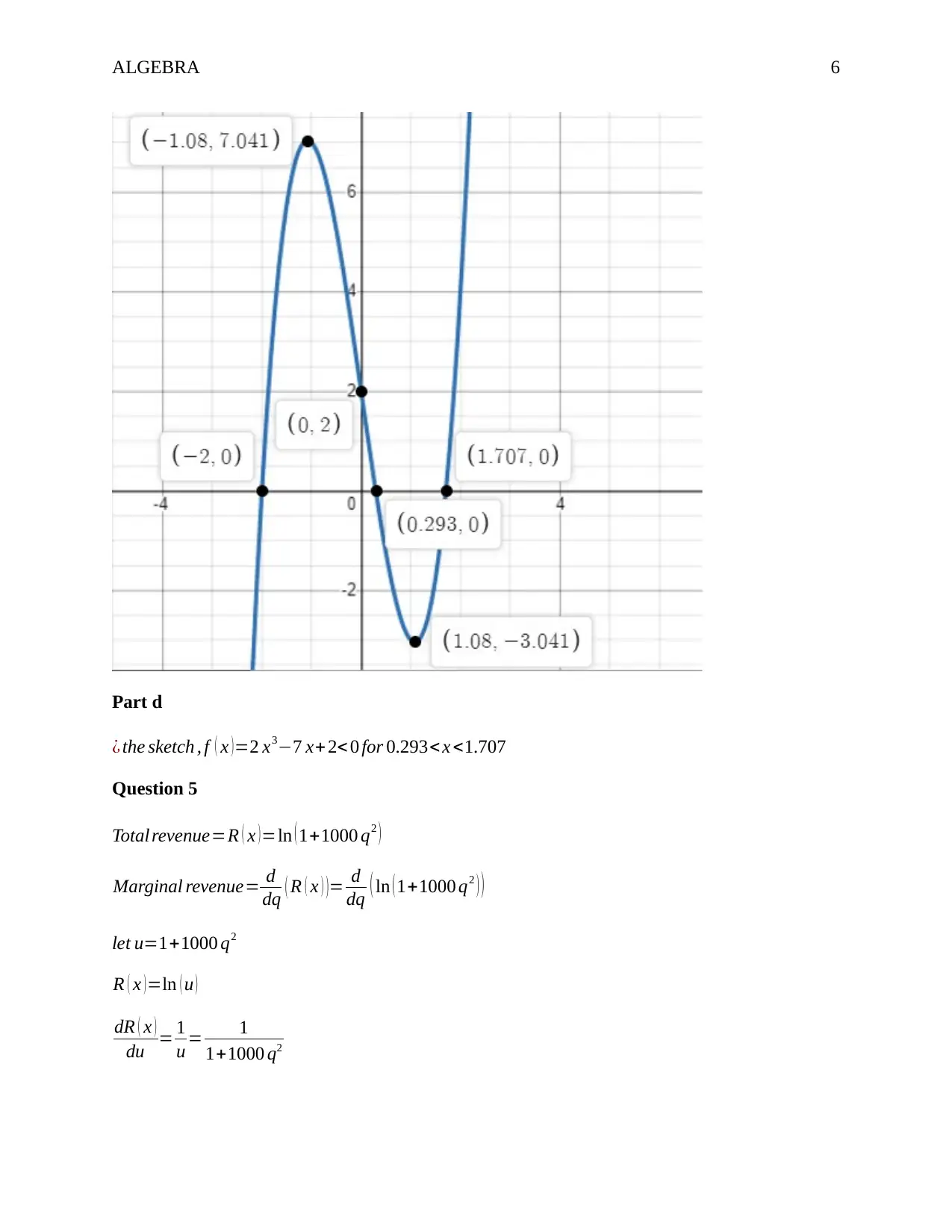
f ( x ) =2 x3−7 x +2=0 when x=−2 , 0.293 ,∧1.707
Part c
The sketch of the function is shown below
15+20 cos ( π t
12 − π
2 − π
2 )=15+sin ( πt
12 − π
2 )
H=15+sin ( πt
12 − π
2 )=A +B ¿
Therefore , A=15∧C= π
12
Question 4
f ( x )=2 x3−7 x +2
Part a
f ( 0 )=2(0)3−7 ( 0 ) +2=2
f ( 1 ) =2(1)3 −7 ( 1 )+ 2=2−7 +2=−3
f (−1 )=2(−1)3−7 (−1 ) +2=−2+ 7+2=7
f ( −2 ) =2(−2)3−7 ( −2 ) +2=−16+14+2=0
Part b
f ( x ) =2 x3−7 x +2=0 when x=−2 , 0.293 ,∧1.707
Part c
The sketch of the function is shown below
ALGEBRA 6
Part d
¿ the sketch , f ( x )=2 x3−7 x+ 2< 0 for 0.293< x <1.707
Question 5
Total revenue=R ( x ) =ln ( 1+1000 q2 )
Marginal revenue= d
dq ( R ( x ) )= d
dq ( ln ( 1+1000 q2 ) )
let u=1+1000 q2
R ( x )=ln ( u )
dR ( x )
du = 1
u = 1
1+1000 q2
Part d
¿ the sketch , f ( x )=2 x3−7 x+ 2< 0 for 0.293< x <1.707
Question 5
Total revenue=R ( x ) =ln ( 1+1000 q2 )
Marginal revenue= d
dq ( R ( x ) )= d
dq ( ln ( 1+1000 q2 ) )
let u=1+1000 q2
R ( x )=ln ( u )
dR ( x )
du = 1
u = 1
1+1000 q2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

ALGEBRA 7
du
dq =0+ 1000 ( 2 ) q2−1=2000 q
dR ( x )
dq = dR ( x )
du × du
dq = 1
1+1000 q2 ×2000 q= 2000 q
1+1000 q2
Marginal revenue= 2000 q
1+1000 q2
Marginal revenue ( q=10 )= 2000 ( 10 )
1+1000 ( 10 )2
¿ 20000
1+100000 = 20000
100001 =0.199998=$ 0.2
Marginal revenue=$ 0.2 shows that the additional revenue obtained when selling 10 units of
goods ( q=10 ).
Question 6
Part a
f ( x )=x3 +2
x -1 0 1 2
f ( x ) 1 2 3 10
du
dq =0+ 1000 ( 2 ) q2−1=2000 q
dR ( x )
dq = dR ( x )
du × du
dq = 1
1+1000 q2 ×2000 q= 2000 q
1+1000 q2
Marginal revenue= 2000 q
1+1000 q2
Marginal revenue ( q=10 )= 2000 ( 10 )
1+1000 ( 10 )2
¿ 20000
1+100000 = 20000
100001 =0.199998=$ 0.2
Marginal revenue=$ 0.2 shows that the additional revenue obtained when selling 10 units of
goods ( q=10 ).
Question 6
Part a
f ( x )=x3 +2
x -1 0 1 2
f ( x ) 1 2 3 10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
ALGEBRA 8
Part b
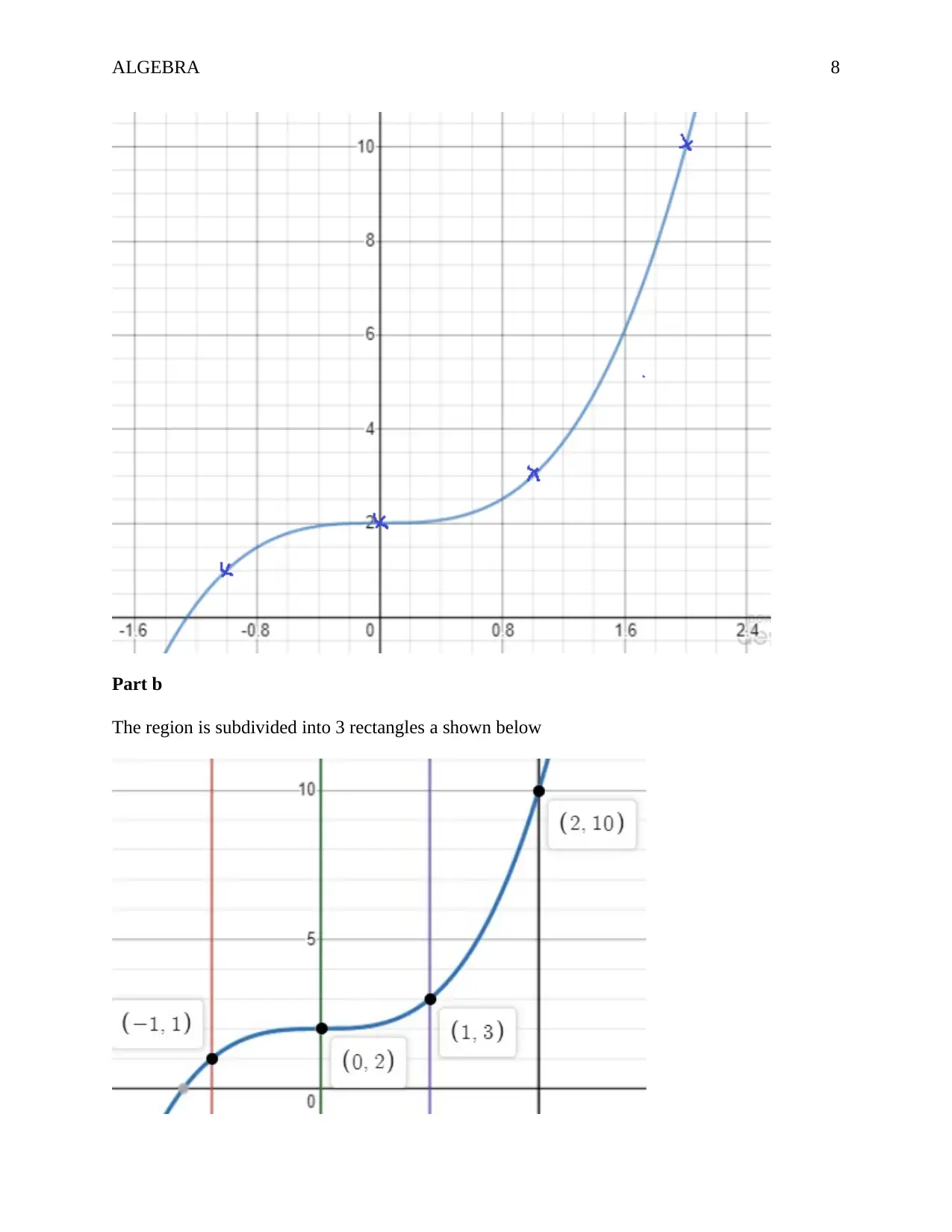
The region is subdivided into 3 rectangles a shown below
Part b
The region is subdivided into 3 rectangles a shown below

ALGEBRA 9
Upper ∑ ¿ ∑
x=−1
x=2
( rectangleheight × rectangle width)
Upper ∑ ¿ 1 ×2+1 ×3+1 ×10
Upper ∑ ¿ 2+3+ 10=15 square units
Part c
The estimation could be improved by increasing the number of subdivisions.
Question 7
Part a
h ( x )=50+ 45 sin ( πx
50 )0 ≤ x ≤ 105
h' ( x )= d
dx (50+ 45 sin ( πx
50 ) )
¿ 45 × π
50 cos ( πx
50 )
h' ( x )=0.9 π cos ( πx
50 )
Part b
h' ( x )=0.9 π cos ( πx
50 )
h' ( 40 ) =0.9 π cos ( π (40)
50 )=0.9 π cos ( 0.8 π ) =−2.28744
The slope of the “amusement park ride” at the point x=40 meters from the starting point is
-2.28744.
Part c
The maximum and minimum height occurs when h' ( x )=0
Upper ∑ ¿ ∑
x=−1
x=2
( rectangleheight × rectangle width)
Upper ∑ ¿ 1 ×2+1 ×3+1 ×10
Upper ∑ ¿ 2+3+ 10=15 square units
Part c
The estimation could be improved by increasing the number of subdivisions.
Question 7
Part a
h ( x )=50+ 45 sin ( πx
50 )0 ≤ x ≤ 105
h' ( x )= d
dx (50+ 45 sin ( πx
50 ) )
¿ 45 × π
50 cos ( πx
50 )
h' ( x )=0.9 π cos ( πx
50 )
Part b
h' ( x )=0.9 π cos ( πx
50 )
h' ( 40 ) =0.9 π cos ( π (40)
50 )=0.9 π cos ( 0.8 π ) =−2.28744
The slope of the “amusement park ride” at the point x=40 meters from the starting point is
-2.28744.
Part c
The maximum and minimum height occurs when h' ( x )=0
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

ALGEBRA 10
h' ( x )=0.9 π cos ( πx
50 )=0
cos ( πx
50 )= 0
0.9 π =0
πx
50 =co s−1 0=90= π
2 ∨27 0= 3 π
2
πx
50 = π
2 , 3 π
2
When πx
50 = π
2 , x= π
2 × 50
π =25
When πx
50 = 3 π
2 , x =3 π
2 × 50
π =75
When x=25 , h ( x )=50+ 45 sin ( 25 π
50 )=50+ 45× 1=95
When x=7 5 , h ( x )=50+ 45sin (75 π
50 )=50+45 ×(−1)=5
Therefore, the maximum height is 95m while the minimum height is 5m.
Part d
h' ' ( x ) =−45 ( π
50 )
2
sin ( π x
50 ) =0
sin ( πx
50 )=0
πx
50 =sin−1 0=0∨π ∨2 π
πx
50 =0 , π ,2 π
When πx
50 =0 , x=0
When πx
50 =π , x =π × 50
π =50
h' ( x )=0.9 π cos ( πx
50 )=0
cos ( πx
50 )= 0
0.9 π =0
πx
50 =co s−1 0=90= π
2 ∨27 0= 3 π
2
πx
50 = π
2 , 3 π
2
When πx
50 = π
2 , x= π
2 × 50
π =25
When πx
50 = 3 π
2 , x =3 π
2 × 50
π =75
When x=25 , h ( x )=50+ 45 sin ( 25 π
50 )=50+ 45× 1=95
When x=7 5 , h ( x )=50+ 45sin (75 π
50 )=50+45 ×(−1)=5
Therefore, the maximum height is 95m while the minimum height is 5m.
Part d
h' ' ( x ) =−45 ( π
50 )
2
sin ( π x
50 ) =0
sin ( πx
50 )=0
πx
50 =sin−1 0=0∨π ∨2 π
πx
50 =0 , π ,2 π
When πx
50 =0 , x=0
When πx
50 =π , x =π × 50
π =50
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

ALGEBRA 11
When πx
50 =2 π , x=2 π × 50
π =10 0
Rate of change , h' ( 0 )=0.9 π cos ( 0 π
50 )=0.9 π
Rate of change , h' ( 50 ) =0.9 π cos ( 50 π
50 )=−0.9 π
Rate of change , h' ( 10 0 ) =0.9 π cos ( 100 π
50 ) =0.9 π
Therefore, the rate of change is greatest when the horizontal distance is 0m and 100m from the
origin.
When πx
50 =2 π , x=2 π × 50
π =10 0
Rate of change , h' ( 0 )=0.9 π cos ( 0 π
50 )=0.9 π
Rate of change , h' ( 50 ) =0.9 π cos ( 50 π
50 )=−0.9 π
Rate of change , h' ( 10 0 ) =0.9 π cos ( 100 π
50 ) =0.9 π
Therefore, the rate of change is greatest when the horizontal distance is 0m and 100m from the
origin.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




