Algebra 2 Assignment: Systems of Equations, Functions, and Logarithms

This Algebra 2 assignment solution provides step-by-step solutions to a variety of algebraic problems. The solutions cover topics including solving linear equations related to health club memberships and tablet price calculations, graphing inequalities on a number line, evaluating functions at different points, and solving systems of equations both algebraically and graphically. Furthermore, the solution demonstrates how to find the center, vertices, equations of asymptotes, and foci of a given equation. It also covers simplifying logarithmic expressions using logarithm properties, writing equations of lines, finding the domain of a function, and converting between exponential and logarithmic forms. Each problem is clearly explained with detailed algebraic steps, making it a valuable resource for students studying algebra.

Running head: ALGEBRA
ALGEBRA
Name of the Student
Name of the University
Author Note

1ALGEBRA
Solve algebraically.
1. Energy Cardio offers membership for a fee of $50 plus a monthly
fee of $20. Exercise Duo offers membership for a fee of $100 plus
a monthly fee $15. After how many months will the total cost of
each health club be the same? What will be the total cost of each
health club?
Solution: Let the month after the cost of each health will become same =
y.
Let the Amount after the ‘y’ months is x.
Hence algebraically,
There will be two equation for two scenarios,
50 + 20y = x ---------(i)
100 + 15y = x ---------(ii)
Solving equations,
 x = 50 + 20y = 100 + 15y
 50 + 20y = 100 + 15y
 20y – 15y = 100 – 50
 5y = 50
 y = 10
hence the month will be 10.
Putting the value of y in equation (i),
 50 + 20*(10) = x
 x = 250 Ans.
2. After a 20% reduction, you buy a tablet for $160. What was the
tablet’s price before the reduction?
Let the tablet’s price before reduction = x.
Hence, According to question,
 x – 20% of x = 160
 x – 20x/100 = 160
 x – x/5 = 160
 (5x-x)/5 = 160
 4x/5 = 160
 4x = 160*5
 x = (160*5)/4

2ALGEBRA
 x = 200 Ans.
Graph on a number line:
3. (-2, 6)
4. Evaluate the function at the given values of the independent
variable and simplify.
F(x)=2x +4
a. f (-x) b. f (5) c. f(x+2)
a. solution:
=> f(-x) = 2(-x) +4
=> f(-x) = 4 -2x Ans.
b. solution:
=> f(5) = 2*5 + 4
=> f(5) = 14 Ans.
c. solution:
=> f(x+2) = 2(x+2) + 4
=> f(x+2) = 2x +4 +4
=> f(x+2) = 2x + 8 Ans.
5. On a piece of graph paper, solve the following system of
equations graphically.
Y=2x +3 ----- (i)
X + y = 0 ------(ii)
Solution:
For equation (i)
Let x = 1

3ALGEBRA
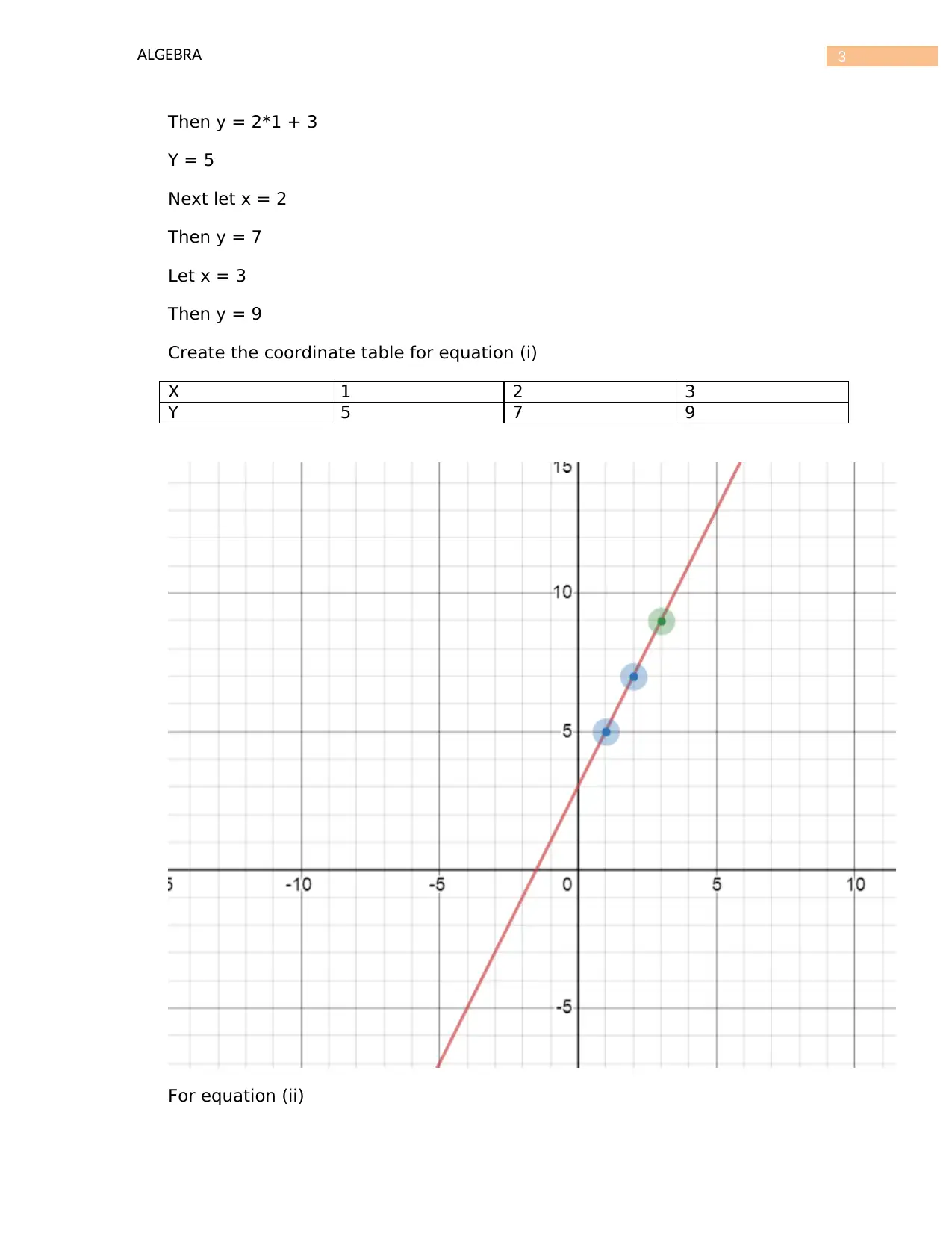
Then y = 2*1 + 3
Y = 5
Next let x = 2
Then y = 7
Let x = 3
Then y = 9
Create the coordinate table for equation (i)
X 1 2 3
Y 5 7 9
For equation (ii)

4ALGEBRA
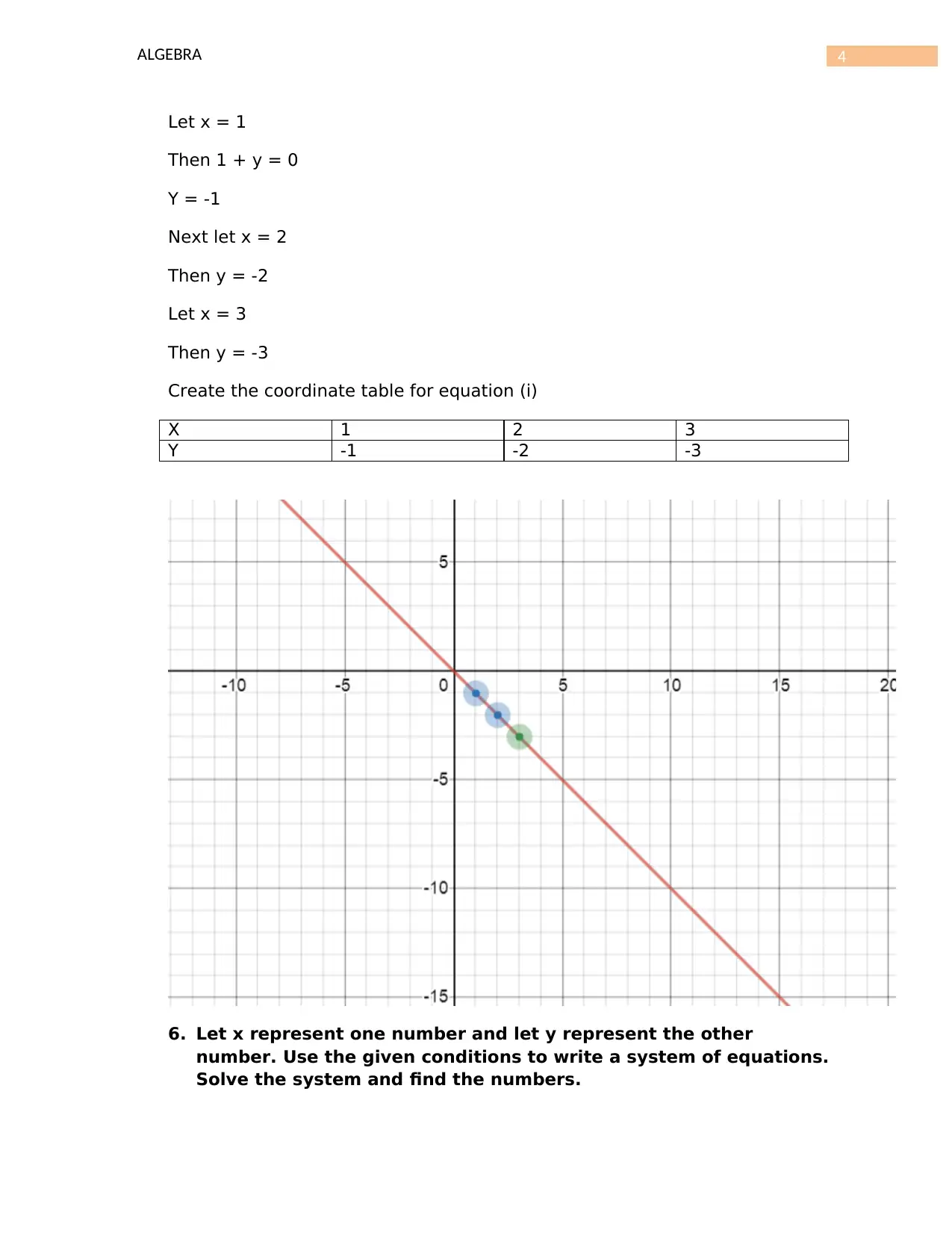
Let x = 1
Then 1 + y = 0
Y = -1
Next let x = 2
Then y = -2
Let x = 3
Then y = -3
Create the coordinate table for equation (i)
X 1 2 3
Y -1 -2 -3
6. Let x represent one number and let y represent the other
number. Use the given conditions to write a system of equations.
Solve the system and find the numbers.

5ALGEBRA
The sum of three times a first number and twice a second
number is 8. If the second number is subtracted from twice the first
number, the result is 3. Find the numbers.
Let the first number be ‘x’ and second number be ‘y’. hence, according to the
question there will be two equations,
3x + 2y = 8 ------(i)
2x – y = 3 -----(ii)
Substitute value y from (ii) and put the value of y in (i),
2x – y = 3
y = 2x – 3
 3x + 2(2x-3) = 8
 3x + 4x – 6 = 8
 7x = 14
 X = 2
Now put the value of x in equation (ii),
 3(2) + 2y = 8
 2y = 8-6
 Y = 1 Ans.
Hence the value of first number is 2 and second number is 1.
7. State the center, vertices, equations of asymptotes and the foci
of the following equation.
x2
9 - y2
25 =1
Solution:
Looking at the denominators, a2 = 9 and b2 = 25, so a = 3 and b = 5.
The equation c2 – a2 = b2 tells that c2 = 9 + 25 = 34, so c = 341/2.

6ALGEBRA
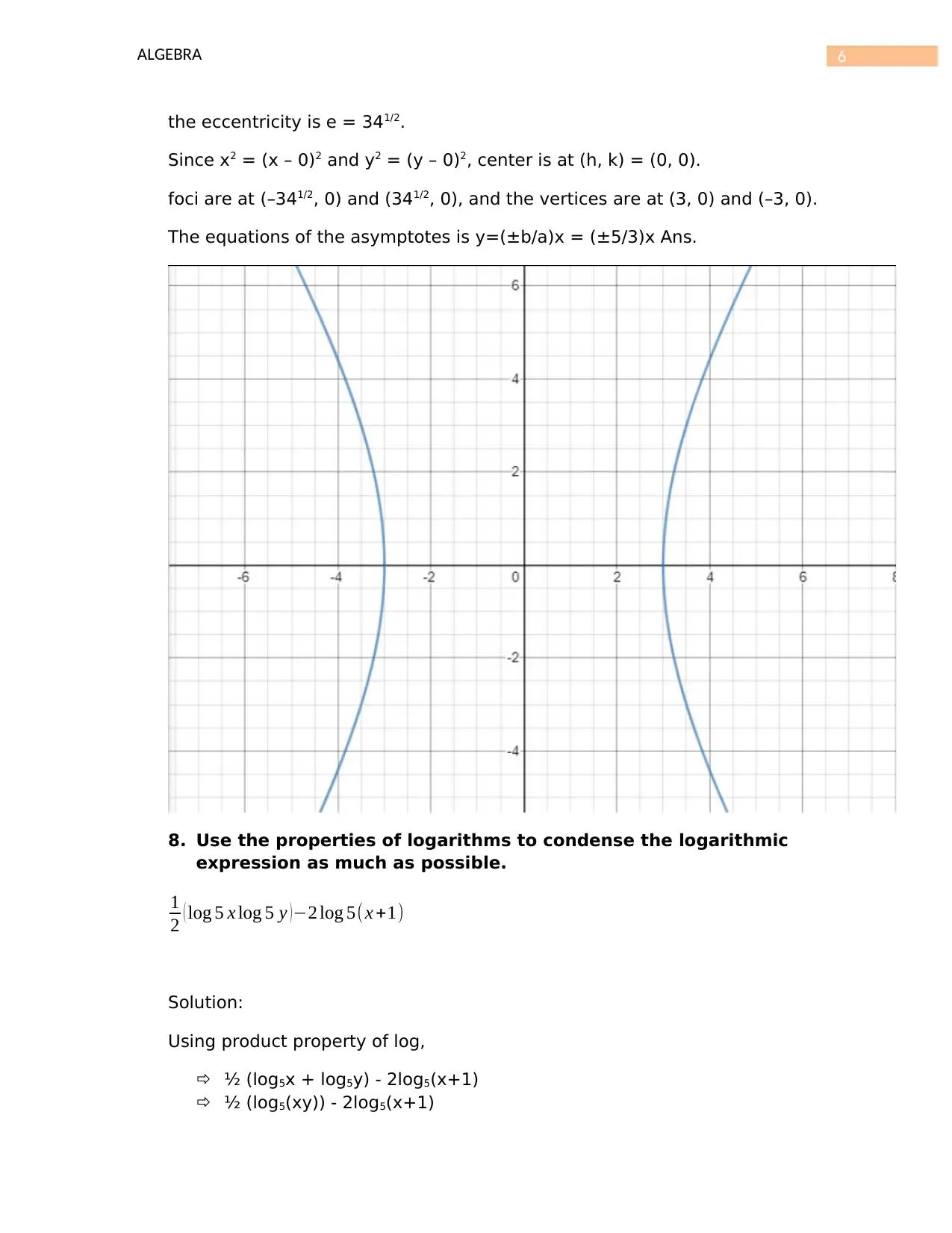
the eccentricity is e = 341/2.
Since x2 = (x – 0)2 and y2 = (y – 0)2, center is at (h, k) = (0, 0).
foci are at (–341/2, 0) and (341/2, 0), and the vertices are at (3, 0) and (–3, 0).
The equations of the asymptotes is y=(±b/a)x = (±5/3)x Ans.
8. Use the properties of logarithms to condense the logarithmic
expression as much as possible.
1
2 ( log 5 x log 5 y )−2 log 5(x +1)
Solution:
Using product property of log,
 ½ (log5x + log5y) - 2log5(x+1)
 ½ (log5(xy)) - 2log5(x+1)

7ALGEBRA
Send the ½ and 2 inside the log,
 log5(x1/2y1/2) - log5(x+1)2
 log5(x1/2y1/2/(x+1)2) Ans.
9. Write an equation for the line that passes through (-1, -3) and is
parallel to the line whose equation is
Y = - 4x + 3.
Solution: according to the slope intercept form,
m (slope) = -4
y1 = - 3
x1 = -1
hence y = mx + c
 (y-y1)/(x-x1) = m
 (y+3)/(x+1) = -4
 Y+3 = -4x -4
 Y = -4x -7 Ans.
10. Find the domain of the function
f (x)= 1
x +7 + 3
x−9
Solution:
find the all possible value for the x, where x-7≠0 and x-9≠0
In the cases, x≠7 and x≠9 hence the domain will be
D(-∞, 7) U (8) U (9, ∞) Ans.
11. Write in its equivalent form logx125 = 3
Also find the value(s) of x.
For logarithmic equations,
Logb(x)=y is equivalent to by = x such that x>0, b>0, and b≠1.
Hence, it can be represented as equivalent for of,
X3 = 125
Solving the expression,

8ALGEBRA
 X3 = 53
 X = 5 Ans.
12. Write in its equivalent logarithmic form: 3
√8=2
 ∛(8 )=2
 81/3 = 2
For logarithmic equations,
Logb(x)=y is equivalent to by = x such that x>0, b>0, and b≠1.
Hence, it can be represented as equivalent for of,
 Log82 = 1/3 Ans.