Algebra Assignment: Solving Equations, Graphing, and Geometry Problems

This document presents a comprehensive solution set for an algebra homework assignment. The solutions cover a wide range of topics, including solving algebraic expressions, simplifying equations, and working with linear and quadratic functions. The assignment explores the relationship between speed, distance and time, as well as solving equations involving ratios and algebraic expressions. It also delves into graphing linear and quadratic equations, finding intercepts, and determining the area of rectangles and triangles. Furthermore, the assignment addresses the concept of the discriminant in quadratic equations, and includes the solution of simultaneous equations. The document provides a step-by-step approach to problem-solving, including the application of formulas, factorization, and the quadratic formula. Overall, the assignment covers fundamental concepts in algebra, providing a solid foundation for further mathematical studies. This assignment is contributed by a student to be published on the website Desklib. Desklib is a platform which provides all the necessary AI based study tools for students.

Part – A
Solution 1: Given the expression , where U and S are speed and distance
respectively. Note that both speed and distance are depends on time t, so S and U are
dependent variables and time t is independent variable.
Solution 2a): Given that the ratio of x to the sum of x and 5 is 6. So the algebraic
expression is
Now
Simplify further,
Hence
Solution 2b): Given that doubling the result 4 less than x is 6 so the algebraic expression
is
Now,
Hence
Solution 2c): Given that 6 more than half of x is 6 so the algebraic expression is
Now,
Hence
Solution 3a): Given the expression .
Now,
Hence,
Solution 3b): Given the expression .
Now,

Simplify further,
Hence,
Solution 4a): Given the expression .
Now,
Use formula we get,
Solution 4b): Given the expression .
Now use factorization method
Hence
Solution 5: Consider the expression -------- (1)
Now,
Simplify further,
Hence
Solution 6: Given that the expression

Rearranging the above expression, we get
Squaring the both sides of above equation and simplify we get,
Hence equation y as function of x is
Now, substitute in above equation and simplify
Simplify further,
Hence, when
Solution 7a): Given the points . We need to find an equation that
passes through these three points. Suppose that the expression in terms of x and y will be
------ (1)
Our firs aim is to find the unknown a, b and c.
Since equation (1) passes through point , that is at
Use these values in equation (1), we get
Again equation (1) passes through point that is at
Use these values in equation (1), we get
Since so -------- (2)
Again equation (1) passes through point that is at
Use these values in equation (1), we get
Since so ------- (3)
Equation (2) and (3) gives . Substitute the values of a, b and c in equation
(1), we get the required expression

Solution 7b): Given the points . We need to find an equation that
passes through these three points. Suppose that the expression in terms of x and y will be
------ (1)
Our firs aim is to find the unknown a, b and c.
Since equation (1) passes through point , that is at
Use these values in equation (1), we get
------- (2)
Again equation (1) passes through point that is at
Use these values in equation (1), we get
--------- (3)
Again equation (1) passes through point that is at
Use these values in equation (1), we get
------- (4)
Equation (2), (3) and (4) gives . Substitute the values of a, b and c in
equation (1), we get the required expression
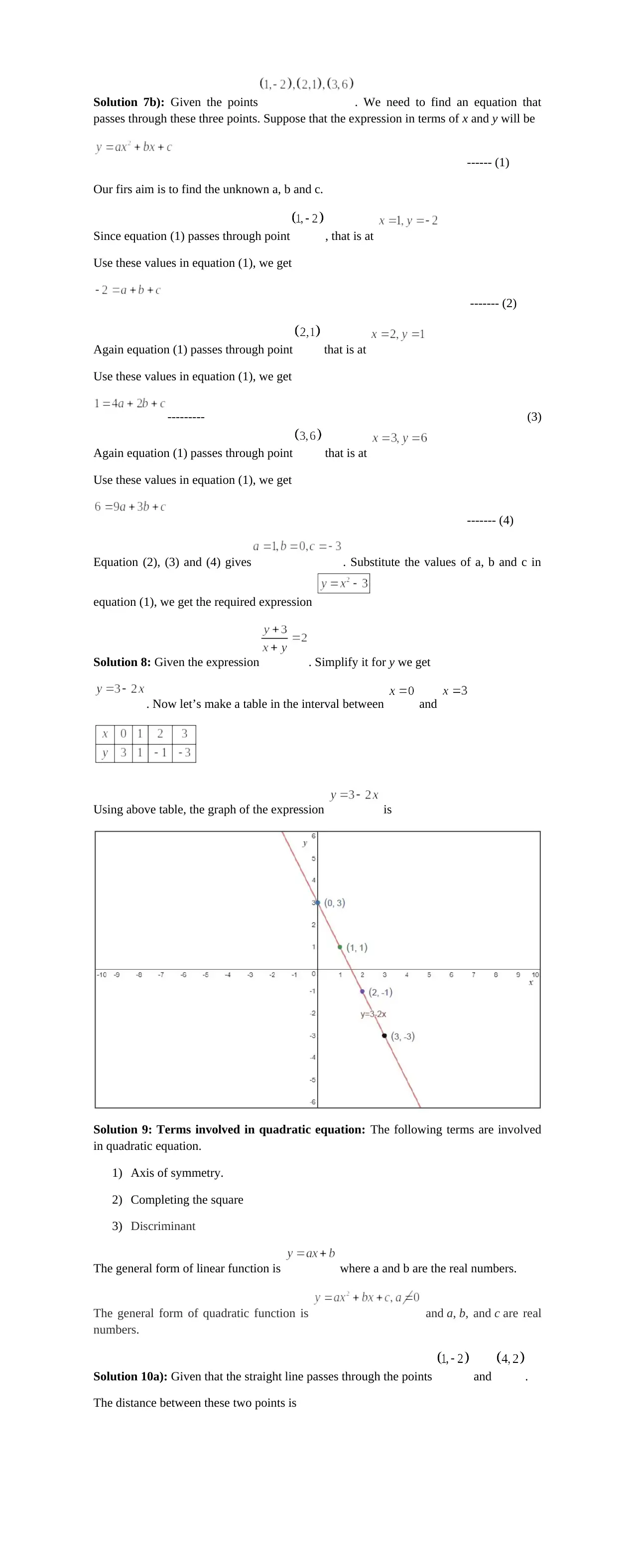
Solution 8: Given the expression . Simplify it for y we get
. Now let’s make a table in the interval between and
Using above table, the graph of the expression is
Solution 9: Terms involved in quadratic equation: The following terms are involved
in quadratic equation.
1) Axis of symmetry.
2) Completing the square
3) Discriminant
The general form of linear function is where a and b are the real numbers.
The general form of quadratic function is and a, b, and c are real
numbers.
Solution 10a): Given that the straight line passes through the points and .
The distance between these two points is

And gradient is
Solution 10b): Given this implies that . The slope of this line is
. Now suppose that be the slope of line perpendicular to
So, this implies that
So, equation of line passing through the point whose slope is
Hence,
Solution 10c): Given that this implies that .The slope of this line
is . Note that two parallel lines have same slope but different intercept. So the
parallel line other than is where c any real number.
Part – B
Solution 1a): Given the straight line , further simplify to get the equation in
the slope-intercept form i.e. , where m is the gradient and x-intercept is
.
Now,
Comparing with
We get and ,
Therefore, gradient is and x-intercept is given by i.e. .
Solution 1b)(i): Given the straight line , further simplifying:
Now,

For x-intercept, put and solve:
So,
x-intercept is
Now, for y-intercept, put and solve:
So, y-intercept is
Solution 1b)(ii): Given the straight line , further simplifying:
Now,
For x-intercept, put and solve:
So,
x-intercept is
Now, for y-intercept, put and solve:
So, y-intercept is
Solution 1b)(iii): Given the straight line , further simplifying:
Now,
For x-intercept, put and solve:
So,
x-intercept is
Now, for y-intercept, put and solve:
So, y-intercept is
Solution 1c): Given that the lengths of the two sides of rectangle A are 4m and 8m.

So, the area of rectangle A is:
Now, each side of rectangle B is x m longer than the corresponding side,
Therefore, the sides of rectangle B will be m and m. Then,
Now, it is given that area of rectangle B is triple the area of rectangle A. i.e.
From here we get,
But x can’t be negative. So,
Therefore, lengths of rectangle B are m and m i.e. and .
Solution 2a): Discriminant of a quadratic equation is given by:
By definition of discriminant:
1) If then the quadratic equation has distinct real roots.
2) If then the quadratic equation has repeated real roots.
3) If then the quadratic equation has non-real roots.
Solution 2b)(i):Let second be the time taken by John who is 100 m away from home
and walks 4 m per second towards home. So, distance for john is:
Now, let second be the time taken by John who is 60 m away from home and walks 2
m per second towards home. So, distance for john is:
Solution 2b)(ii):Suppose they meet x meter before reaching the home and they will both
take equal time.
So, distance covered by John will be and distance covered by Mary will be
Since,
Therefore, time taken by John will be:
And, time taken by Mary will be:
Now,

Now,
So,
Hence, they will meet after
Solution 2b)(iii):Now, John walks 3 m per second towards home. So,
Time taken by John will be:
And, time taken by Mary will be:
Since,
Hence, Mary will arrive home earlier.
Solution 2c): Given pair of simultaneous equations:
…. (1)
And,
…… (2)
Now, multiply equation (2) by 2 and add to equation (1) and get:
Put this value of xin equation (2):
Therefore, we get and .
Solution 3a): Given the equation .
Now use factorization method
Then,

Hence, required solution is
Solution 3b): Given the equation .
Now, use quadratic formula:
Therefore,
Hence, required solution is
Solution 3c):Given the equation .
Now let’s make a table in the interval between and
x -3 -2 -1 0 1 2 3
y 24 15 8 3 0 -1 0
Using above table, the graph of the expression is
Solution 3d): Given that the line has two intersection points with quadratic
function . Thus, we get
Since, there are two intersection points, so, there will be two distinct real roots for the
above equation and for this discriminant should be positive:
Therefore, the required range of kis .

Solution 4a):From triangle ACB
Therefore, the length BCis
Solution 4b):From triangle ADC
Now, from triangle ACB therefore
Now, in triangle CDB
Since, DE is same as EBand
So,
Now, in triangle EDC, Let
Therefore, the angle DECis
Solution 4c): In triangle EFB, and
And, now
Now, the area of triangle EFB is given by:
Therefore, the required area is