Algebra Assignment: Iterative Methods, Factorization, Binomial Theorem

This algebra assignment solution encompasses several key concepts, including iterative formulas, factorization of cubic equations, binomial expansion, and arithmetic series. The first question involves solving a quadratic equation using an iterative formula, demonstrating the iterative process in a table, and explaining the stopping criteria. The second question focuses on factorizing a cubic polynomial, detailing the steps taken to find the roots and factorize the expression. The third question explores binomial expansion, calculating the first four coefficients of an expansion using the binomial theorem. The final question presents a real-world scenario of a flu virus spreading in a city, converting the information into an arithmetic series, deriving recurrence and nth term formulas, and calculating the number of new infections on specific days. This assignment provides a comprehensive overview of algebraic techniques and their applications.

Algebra

TABLE OF CONTENTS
QUESTION 1..................................................................................................................................1
QUESTION 2..................................................................................................................................2
QUESTION 3..................................................................................................................................5
QUESTION 4..................................................................................................................................7

QUESTION 1
x² – 2x -1 = 0
Range of roots: 2.3 < α < 2.5
i)Show the working to arrive at an iterative formula
Equation given = x² – 2x -1 = 0
x² = 2x +1
On dividing both the sides by x we get
x = 2 + (1/x)
Thus iterative formula can be written as :
x(n+1) = 2 + [ 1/x(n) ]
ii) Include a table to clearly demonstrate the iterative process.
(You are only required to demonstrate the values up to the point whereby your answer is
correct to 4 d.p.)
x(n+1) = 2 + [ 1/x(n) ]
Let the initial value x0 = 2.4
N Xn Xn +1
0 X0 2.4
1 X1 = 2 + (1 / 2.4) 2.4166
2 X2 = 2 + (1 / 2.4166) 2.4138
3 X3 = 2 + (1 / 2.4138) 2.4142
1

4 X4 = 2 + (1 / 2.4138) 2.4142
iii) Explain concisely why you have chosen to stop the iterative process where you have
After fourth iteration the process have been chosen to stop because both third and fourth iteration
have same value up to three decimal points.
iv) use your formula to find the root correct to 4 decimal places.
(You should choose your starting value from the given information)
x = 2 + (1/x)
Let the initial value is x0 = 2.4
From the above table it can be observed that upto 4 iterations are possible thus root is
given by 2.4142
QUESTION 2a) Factorise fully the following cubic; x3 + 4x2 + x – 6
(Ensure you demonstrate relevant working regarding how you obtain your fist root
and any obtained quadratic)
Answer:
Detailed solution :
Step 1 : Equation at the end of step 1
= (((x3) + 22x2) + x) - 6
Step 2: Checking for a perfect cube :
2.1: x3+4x2+x-6
Referring this, it can be stated that it is not a perfect cube
2.2 Factoring: x3+4x2+x-6
2

Expressions are divided into two groups:
Group 1: x-6
Group 2: x3+4x2
Pulling out from each group separately
Group 1: (x-6) * 1
Group 2: (x+4) * (x2)
2.3 Polynomial roots calculation
Finding roots: F (X) = X3+4X2+x-6
When F(x) = 0
In this, leading coefficient accounts for 1
Whereas, trailing constant is 1,2,3,6
P Q P/Q F(P/Q) Divisor
-1 1 -1.00 -4.00
-2 1 -2.00 0.00 x+2
-3 1 -3.00 0.00 x+3
-6 1 -6.00 -84.00
1 1 1.00 0.00 x-1
2 1 2.00 20.00
3 1 3.00 60.00
6 1 6.00 360.00
So: x3+4x2+x-6
2.4 Polynomial long division
3

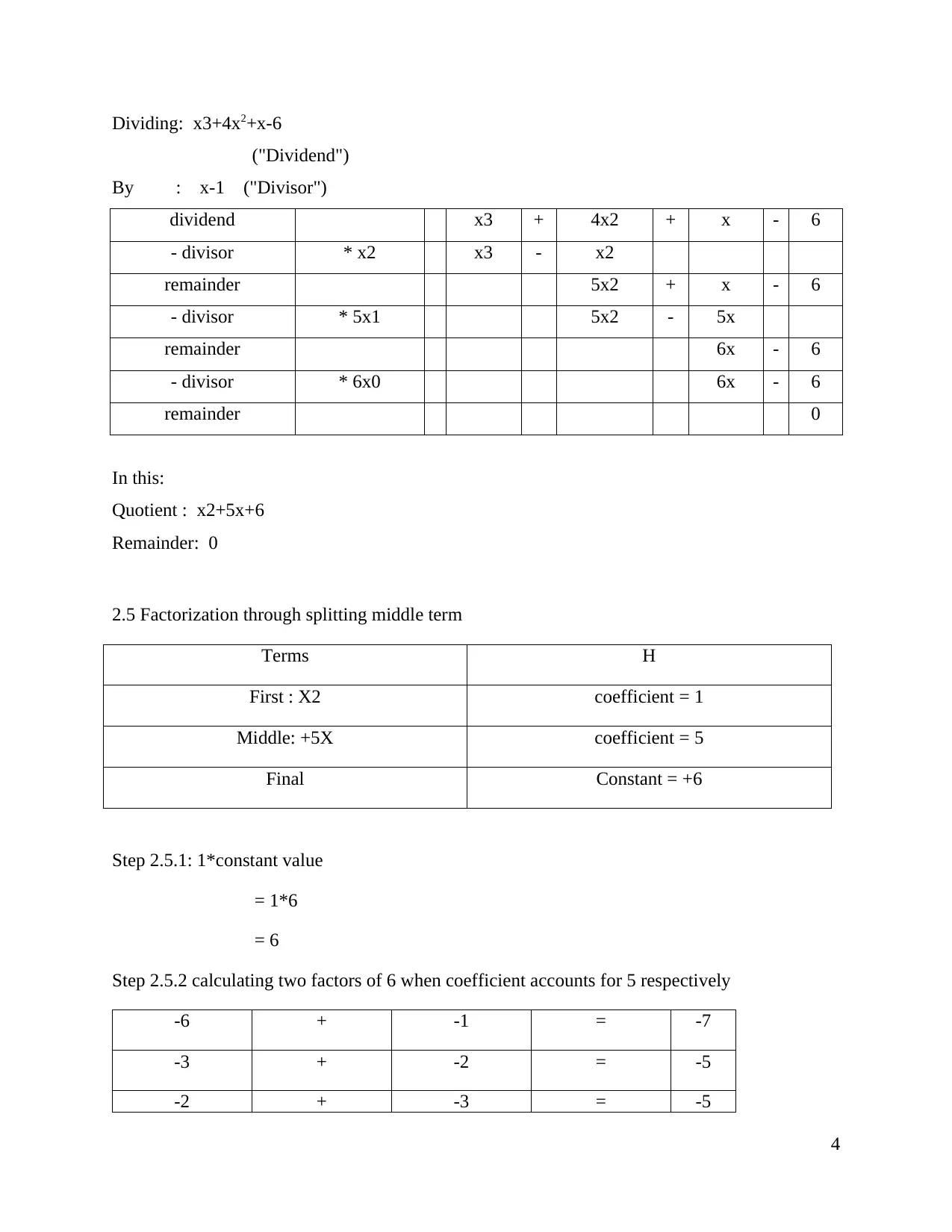
Dividing: x3+4x2+x-6
("Dividend")
By : x-1 ("Divisor")
dividend x3 + 4x2 + x - 6
- divisor * x2 x3 - x2
remainder 5x2 + x - 6
- divisor * 5x1 5x2 - 5x
remainder 6x - 6
- divisor * 6x0 6x - 6
remainder 0
In this:
Quotient : x2+5x+6
Remainder: 0
2.5 Factorization through splitting middle term
Terms H
First : X2 coefficient = 1
Middle: +5X coefficient = 5
Final Constant = +6
Step 2.5.1: 1*constant value
= 1*6
= 6
Step 2.5.2 calculating two factors of 6 when coefficient accounts for 5 respectively
-6 + -1 = -7
-3 + -2 = -5
-2 + -3 = -5
4

-1 + -6 = -7
1 + 6 = 7
2 + 3 = 5
Step 2.5.3 Rewriting polynomial by splitting the middle term using factors 2 & 3
x2 + 2x + 3x + 6
Step 2.5.4
Addition of first two terms: x * (x+2)
Addition of last two terms: 3 * (x+2)
2.5.5 Addition of all the four terms derived in step 4
(x +3) * (x+ 2) * (x-1)
b) State the three values of x for your solutions to part a)
Three values of x are enumerated below:
X +3
x +2
x -1
QUESTION 3
Q.3 (a) Find the 1st 4 coefficients of the expansion of ( a + b )12 by using the binomial
expansion showing relevant working.
Answer:
Formula of binomial expansion: $$$(a+b)^n=\sum_{k=0}^n \binom{n}{k} a^{n-k} b^k$$$,
where $$$\binom{n}{k}=\frac{n!}{(n-k)!k!}$$$ and $$$n!=1 \cdot 2 \cdot 3 ... n$$$.
We have that $$$a=b$$$, $$$b=a$$$, $$$n=12$$$.
5

Therefore:
$$$\left(a + b\right)^{12}=\sum_{k=0}^{12} \binom{12}{k} \left(b\right)^{12-k} \left(a\
right)^k$$$
Computation of product for every value of $$$k$$$
From $$$0$$$ to $$$12$$$.
$$$k=0$$$: $$$\binom{12}{0} \left(b\right)^{12-0} \left(a\right)^{0}=\frac{12!}{(12-0)! 0!}\
left(b\right)^{12} \left(a\right)^{0}=b^{12}$$$
$$$k=1$$$: $$$\binom{12}{1} \left(b\right)^{12-1} \left(a\right)^{1}=\frac{12!}{(12-1)! 1!}\
left(b\right)^{11} \left(a\right)^{1}=12 a b^{11}$$$
$$$k=2$$$: $$$\binom{12}{2} \left(b\right)^{12-2} \left(a\right)^{2}=\frac{12!}{(12-2)! 2!}\
left(b\right)^{10} \left(a\right)^{2}=66 a^{2} b^{10}$$$
$$$k=3$$$: $$$\binom{12}{3} \left(b\right)^{12-3} \left(a\right)^{3}=\frac{12!}{(12-3)! 3!}\
left(b\right)^{9} \left(a\right)^{3}=220 a^{3} b^{9}$$$
$$$k=4$$$: $$$\binom{12}{4} \left(b\right)^{12-4} \left(a\right)^{4}=\frac{12!}{(12-4)! 4!}\
left(b\right)^{8} \left(a\right)^{4}=495 a^{4} b^{8}$$$
$$$k=5$$$: $$$\binom{12}{5} \left(b\right)^{12-5} \left(a\right)^{5}=\frac{12!}{(12-5)! 5!}\
left(b\right)^{7} \left(a\right)^{5}=792 a^{5} b^{7}$$$
$$$k=6$$$: $$$\binom{12}{6} \left(b\right)^{12-6} \left(a\right)^{6}=\frac{12!}{(12-6)! 6!}\
left(b\right)^{6} \left(a\right)^{6}=924 a^{6} b^{6}$$$
$$$k=7$$$: $$$\binom{12}{7} \left(b\right)^{12-7} \left(a\right)^{7}=\frac{12!}{(12-7)! 7!}\
left(b\right)^{5} \left(a\right)^{7}=792 a^{7} b^{5}$$$
$$$k=8$$$: $$$\binom{12}{8} \left(b\right)^{12-8} \left(a\right)^{8}=\frac{12!}{(12-8)! 8!}\
left(b\right)^{4} \left(a\right)^{8}=495 a^{8} b^{4}$$$
$$$k=9$$$: $$$\binom{12}{9} \left(b\right)^{12-9} \left(a\right)^{9}=\frac{12!}{(12-9)! 9!}\
left(b\right)^{3} \left(a\right)^{9}=220 a^{9} b^{3}$$$
$$$k=10$$$: $$$\binom{12}{10} \left(b\right)^{12-10} \left(a\right)^{10}=\frac{12!}{(12-10)!
10!}\left(b\right)^{2} \left(a\right)^{10}=66 a^{10} b^{2}$$$
$$$k=11$$$: $$$\binom{12}{11} \left(b\right)^{12-11} \left(a\right)^{11}=\frac{12!}{(12-11)!
11!}\left(b\right)^{1} \left(a\right)^{11}=12 a^{11} b$$$
6

$$$k=12$$$: $$$\binom{12}{12} \left(b\right)^{12-12} \left(a\right)^{12}=\frac{12!}{(12-12)!
12!}\left(b\right)^{0} \left(a\right)^{12}=a^{12}$$$
So:
$$$\left(a + b\right)^{12}=\sum_{k=0}^{12} \binom{12}{k} \left(b\right)^{12-k} \left(a\
right)^k=\binom{12}{0} \left(b\right)^{12-0} \left(a\right)^{0}+\binom{12}{1} \left(b\
right)^{12-1} \left(a\right)^{1}+\binom{12}{2} \left(b\right)^{12-2} \left(a\right)^{2}+\
binom{12}{3} \left(b\right)^{12-3} \left(a\right)^{3}+\binom{12}{4} \left(b\right)^{12-4} \
left(a\right)^{4}+\binom{12}{5} \left(b\right)^{12-5} \left(a\right)^{5}+\binom{12}{6} \left(b\
right)^{12-6} \left(a\right)^{6}+\binom{12}{7} \left(b\right)^{12-7} \left(a\right)^{7}+\
binom{12}{8} \left(b\right)^{12-8} \left(a\right)^{8}+\binom{12}{9} \left(b\right)^{12-9} \
left(a\right)^{9}+\binom{12}{10} \left(b\right)^{12-10} \left(a\right)^{10}+\binom{12}{11} \
left(b\right)^{12-11} \left(a\right)^{11}+\binom{12}{12} \left(b\right)^{12-12} \left(a\
right)^{12}=a^{12} + 12 a^{11} b + 66 a^{10} b^{2} + 220 a^{9} b^{3} + 495 a^{8} b^{4} +
792 a^{7} b^{5} + 924 a^{6} b^{6} + 792 a^{5} b^{7} + 495 a^{4} b^{8} + 220 a^{3} b^{9}
+ 66 a^{2} b^{10} + 12 a b^{11} + b^{12}$$$
Final answer: $$$\left(a + b\right)^{12}=a^{12} + 12 a^{11} b + 66 a^{10} b^{2} + 220
a^{9} b^{3} + 495 a^{8} b^{4} + 792 a^{7} b^{5} + 924 a^{6} b^{6} + 792 a^{5} b^{7} +
495 a^{4} b^{8} + 220 a^{3} b^{9} + 66 a^{2} b^{10} + 12 a b^{11} + b^{12}$$$
b.Using the values; a = 3 and b = 2x
calculate the 1st 4 terms of the complete expansion in ascending powers of x
$$$\left(3 + 2X\right)^{12}=3^{12} + 12 (3)^{11} 2x + 66 (3)^{10} 2x^{2} + 220 (3)^{9}
2x^{3} + 495 (3)^{8} 2x^{4} + 792 3^{7} 2x^{5} + 924 (3)^{6} 2x^{6} + 792 (3)^{5} 2x^{7} +
495 (3)^{4} 2x^{8} + 220 (3)^{3} 2x^{9} + 66 (3)^{2} 2x^{10} + 12 (3) (2x)^{11} + 2x^{12}$
$$
QUESTION 4
In a city a flu virus with infects 2 additional people each day over a 6- week winter period.
7

A. Convert this information into an appropriate arithmetic mathematical series showing
how many people are infected over the first week (You will do this through forming and
solving a linear algebraic equation) .
Solution
Let the number of infected people on first day of first week is: x
As additional two people are infected on each day the infected people on day 2 is : (x +2 )
Similarly number of people infected on further days is:
Day 3: (x +2 ) +2 = x +4
Thus for the entire week (7 days ) a series can be form as:
x, (x +2 ), (x +4), (x +6 ) ,(x +8 ) , (x +10 ), (x +12 )
Thus the total number of infected people over the entire week is = Sum of the above series
= x + (x +2 ) + (x +4)+ (x +6 ) +(x +8 ) + (x +10 ) + (x +12 )
= 7x + 42
Number of infected people over entire first week = 7x + 42
Since each day virus infects two people the number of people infected on day one can be
considered as equals to 2
Thus x = 2
On substituting this on above equation we get
Number of infected people over entire first week = 7x + 42 = 7(2) +42 = 56
Hence 56 people were infected over first week.
B. Produce two linear mathematical formulas demonstrating;
1. The recurrence formula to calculate the next term using the notation; un and un+1
The first term = Un
8

Second term = U(n+1)
The common ratio (d) for the recurrence formula is = U(n+1) - Un
Thus the next term can be determine by the formula:
Third term = U(n+1) + d
2. The formula to calculate the nth term
The series formulated above can be considered as an arithmetic progression and its n term
can be calculated by the following formula.
A(n)= a + (n-1)*d
Where n is the term to be determine
a is the first term of series
d is the common difference between the terms of series
C. Calculate the number of new people who will catch the virus;
From the above section the series formulated as :
x, (x +2 ), (x +4), (x +6 ) ,(x +8 ) , (x +10 ), (x +12 )
On putting x = 2
Series becomes: 2, 4, 6, 8, 10, 12, 14
Each element in series represents number of people infected on particular day
1. On the 16th day.
N = a+(N-1)*d
N(16)= a+(16-1)*d
a=2 ; d= 2; N= 16
On putting these values in equation we get:
9