Algebra Assignment: Equations, Functions, and Applications
VerifiedAdded on 2020/03/04
|22
|1984
|220
Homework Assignment
AI Summary
This document provides a comprehensive set of solutions to an algebra assignment, covering a wide range of topics. The solutions begin with basic concepts like evaluating functions and graphing, progressing to more complex topics such as exponential and logarithmic functions, including applications to population growth and carbon dating. The assignment explores various algebraic techniques for solving equations, interpreting graphs, and applying mathematical models to real-world scenarios. The solutions include detailed explanations, calculations, and graphs to illustrate the concepts. The document also includes references to relevant algebra textbooks. Overall, the assignment aims to provide students with a thorough understanding of algebraic principles and their practical applications.

Algebra
1 | P a g e
Mathematics
1 | P a g e
Mathematics
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Algebra
Contents
Solution-1).......................................................................................................................................3
Solution-2).......................................................................................................................................4
Solution-3).......................................................................................................................................5
Solution-3a).................................................................................................................................5
Solution-3b).................................................................................................................................6
Solution-3c).................................................................................................................................6
Solution-3d).................................................................................................................................7
Solution-4).......................................................................................................................................7
Solution-4a).................................................................................................................................7
Solution-4b).................................................................................................................................8
Solution-4c).................................................................................................................................8
Solution-4d).................................................................................................................................8
Solution-4e).................................................................................................................................9
Solution-5).......................................................................................................................................9
Solution-6).......................................................................................................................................9
Solution-7).....................................................................................................................................10
Solution-8).....................................................................................................................................11
Solution-8a)...............................................................................................................................11
Solution-8b)...............................................................................................................................11
Solution-9).....................................................................................................................................13
Solution-10)...................................................................................................................................13
Solution-11)...................................................................................................................................14
Solution-11a).............................................................................................................................14
Solution-11b).............................................................................................................................14
Solution-12)...................................................................................................................................14
Solution-12a).............................................................................................................................14
Solution-12b).............................................................................................................................15
Solution-13)...................................................................................................................................15
Solution-14)...................................................................................................................................16
Solution-15)...................................................................................................................................16
2 | P a g e
Contents
Solution-1).......................................................................................................................................3
Solution-2).......................................................................................................................................4
Solution-3).......................................................................................................................................5
Solution-3a).................................................................................................................................5
Solution-3b).................................................................................................................................6
Solution-3c).................................................................................................................................6
Solution-3d).................................................................................................................................7
Solution-4).......................................................................................................................................7
Solution-4a).................................................................................................................................7
Solution-4b).................................................................................................................................8
Solution-4c).................................................................................................................................8
Solution-4d).................................................................................................................................8
Solution-4e).................................................................................................................................9
Solution-5).......................................................................................................................................9
Solution-6).......................................................................................................................................9
Solution-7).....................................................................................................................................10
Solution-8).....................................................................................................................................11
Solution-8a)...............................................................................................................................11
Solution-8b)...............................................................................................................................11
Solution-9).....................................................................................................................................13
Solution-10)...................................................................................................................................13
Solution-11)...................................................................................................................................14
Solution-11a).............................................................................................................................14
Solution-11b).............................................................................................................................14
Solution-12)...................................................................................................................................14
Solution-12a).............................................................................................................................14
Solution-12b).............................................................................................................................15
Solution-13)...................................................................................................................................15
Solution-14)...................................................................................................................................16
Solution-15)...................................................................................................................................16
2 | P a g e

Algebra
Solution-15a).............................................................................................................................16
Solution-15b).............................................................................................................................16
Solution-16)...................................................................................................................................17
Solution-17)...................................................................................................................................18
Solution-17a).............................................................................................................................18
Solution-17b).............................................................................................................................18
Solution-17c).............................................................................................................................18
Solution-17d).............................................................................................................................18
Solution-17e).............................................................................................................................18
Solution-17f)..............................................................................................................................19
Solution-18)...................................................................................................................................19
Solution-19)...................................................................................................................................20
Solution-20)...................................................................................................................................21
References......................................................................................................................................21
3 | P a g e
Solution-15a).............................................................................................................................16
Solution-15b).............................................................................................................................16
Solution-16)...................................................................................................................................17
Solution-17)...................................................................................................................................18
Solution-17a).............................................................................................................................18
Solution-17b).............................................................................................................................18
Solution-17c).............................................................................................................................18
Solution-17d).............................................................................................................................18
Solution-17e).............................................................................................................................18
Solution-17f)..............................................................................................................................19
Solution-18)...................................................................................................................................19
Solution-19)...................................................................................................................................20
Solution-20)...................................................................................................................................21
References......................................................................................................................................21
3 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Algebra
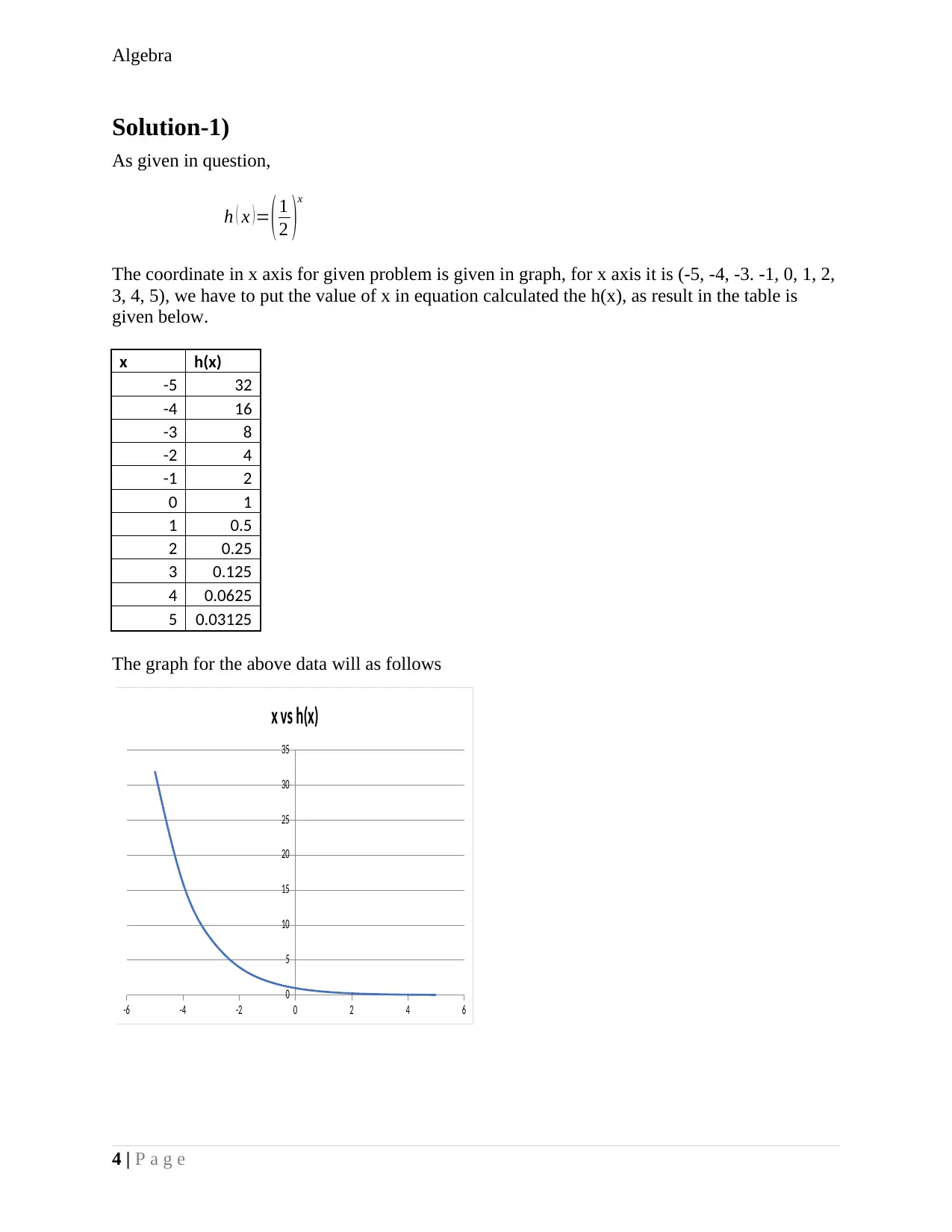
Solution-1)
As given in question,
h ( x )= (1
2 )x
The coordinate in x axis for given problem is given in graph, for x axis it is (-5, -4, -3. -1, 0, 1, 2,
3, 4, 5), we have to put the value of x in equation calculated the h(x), as result in the table is
given below.
x h(x)
-5 32
-4 16
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
4 0.0625
5 0.03125
The graph for the above data will as follows
4 | P a g e
-6 -4 -2 0 2 4 6
0
5
10
15
20
25
30
35
x vs h(x)
Solution-1)
As given in question,
h ( x )= (1
2 )x
The coordinate in x axis for given problem is given in graph, for x axis it is (-5, -4, -3. -1, 0, 1, 2,
3, 4, 5), we have to put the value of x in equation calculated the h(x), as result in the table is
given below.
x h(x)
-5 32
-4 16
-3 8
-2 4
-1 2
0 1
1 0.5
2 0.25
3 0.125
4 0.0625
5 0.03125
The graph for the above data will as follows
4 | P a g e
-6 -4 -2 0 2 4 6
0
5
10
15
20
25
30
35
x vs h(x)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Algebra
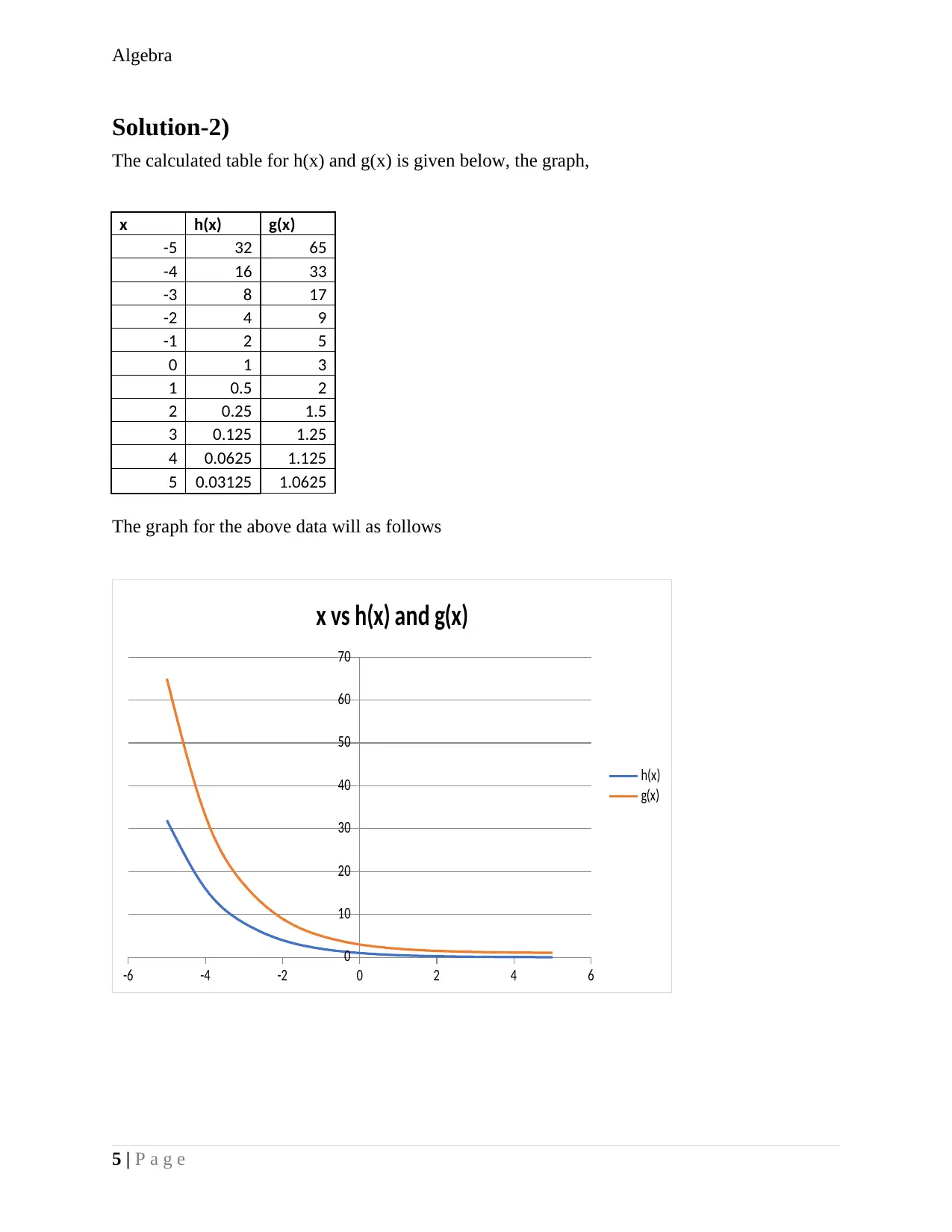
Solution-2)
The calculated table for h(x) and g(x) is given below, the graph,
x h(x) g(x)
-5 32 65
-4 16 33
-3 8 17
-2 4 9
-1 2 5
0 1 3
1 0.5 2
2 0.25 1.5
3 0.125 1.25
4 0.0625 1.125
5 0.03125 1.0625
The graph for the above data will as follows
-6 -4 -2 0 2 4 6
0
10
20
30
40
50
60
70
x vs h(x) and g(x)
h(x)
g(x)
5 | P a g e
Solution-2)
The calculated table for h(x) and g(x) is given below, the graph,
x h(x) g(x)
-5 32 65
-4 16 33
-3 8 17
-2 4 9
-1 2 5
0 1 3
1 0.5 2
2 0.25 1.5
3 0.125 1.25
4 0.0625 1.125
5 0.03125 1.0625
The graph for the above data will as follows
-6 -4 -2 0 2 4 6
0
10
20
30
40
50
60
70
x vs h(x) and g(x)
h(x)
g(x)
5 | P a g e

Algebra
Solution-3)
As given in question,
The accumulated value of investment can be given by the formula
A=P (1+ r
n )nt
……….(i)
Solution-3a)
Where P = Principal,
r = rate per annum,
n = is compounding period for semi-annually = 2, Putting the other value in equation, we get
A=10000 ( 1+ 0.055
2 )
5 x 2
A=10000 (1.311651 ) =13116.51
The total value for semi-annually compounded is = $ 13116.51
Solution-3b)
For compounded quarterly the value of n will be =4, Putting then
P = 10000, r = 0.055, n = 4, and t = 5
Putting the value in above equation
A=10000 ( 1+ 0.055
4 )
5 x 4
A=10000 (1.314067 )=13140.67
For quarterly compounded is approximately $ 13140.67
6 | P a g e
Solution-3)
As given in question,
The accumulated value of investment can be given by the formula
A=P (1+ r
n )nt
……….(i)
Solution-3a)
Where P = Principal,
r = rate per annum,
n = is compounding period for semi-annually = 2, Putting the other value in equation, we get
A=10000 ( 1+ 0.055
2 )
5 x 2
A=10000 (1.311651 ) =13116.51
The total value for semi-annually compounded is = $ 13116.51
Solution-3b)
For compounded quarterly the value of n will be =4, Putting then
P = 10000, r = 0.055, n = 4, and t = 5
Putting the value in above equation
A=10000 ( 1+ 0.055
4 )
5 x 4
A=10000 (1.314067 )=13140.67
For quarterly compounded is approximately $ 13140.67
6 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Algebra
Solution-3c)
Compounded monthly means we have to take n = 12
Putting the values in equation with n = 12
A=10000 (1+ 0.055
12 )5∗12
A=10000 (1.315704 )=13157.04
Therefore, total amount for monthly compounded interest is $ 13157.04
Solution-3d)
The equation for compounded continuously is given as
A=P ert ………. (ii)
We know that, P = 10000, r = 0.055, t = 5
Putting the value in above equation
A = 10000.e (0.055)5
A = 10000 x e0.275 = 13165.31
The accumulated value for the investment = 13165.31
Solution-4)
As given in question,
f ( x)=574(1.026)x This illustrates the population …….(i)
7 | P a g e
Solution-3c)
Compounded monthly means we have to take n = 12
Putting the values in equation with n = 12
A=10000 (1+ 0.055
12 )5∗12
A=10000 (1.315704 )=13157.04
Therefore, total amount for monthly compounded interest is $ 13157.04
Solution-3d)
The equation for compounded continuously is given as
A=P ert ………. (ii)
We know that, P = 10000, r = 0.055, t = 5
Putting the value in above equation
A = 10000.e (0.055)5
A = 10000 x e0.275 = 13165.31
The accumulated value for the investment = 13165.31
Solution-4)
As given in question,
f ( x)=574(1.026)x This illustrates the population …….(i)
7 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Algebra
Solution-4a)
When x = 0, Putting the value of x in above equation
f (0)=574 (1.026)0
f ( 0 ) =574∗1= 574 million
Therefore, India’s population in 1974 is around 574 million
Solution-4b)
When x = 27, the nearest population will be as 2001
Putting the value x = 27
f (27)=574 (1.026)27
f ( 27 ) =574 x 1.9998=1147.87 million
Therefore, population in 2001 is around 1147.87 million
Solution-4c)
Year 2028 means after = 2028-1974 = 54 years from 1974
Putting the value of x = 54
f (54)=574 (1.026)54
f ( 54 )=574 x 3.999=1147.87 million
f ( 54 )=574 x 3.999=2295.46 million
Therefore, in 2028 the population will be 2295 million
8 | P a g e
Solution-4a)
When x = 0, Putting the value of x in above equation
f (0)=574 (1.026)0
f ( 0 ) =574∗1= 574 million
Therefore, India’s population in 1974 is around 574 million
Solution-4b)
When x = 27, the nearest population will be as 2001
Putting the value x = 27
f (27)=574 (1.026)27
f ( 27 ) =574 x 1.9998=1147.87 million
Therefore, population in 2001 is around 1147.87 million
Solution-4c)
Year 2028 means after = 2028-1974 = 54 years from 1974
Putting the value of x = 54
f (54)=574 (1.026)54
f ( 54 )=574 x 3.999=1147.87 million
f ( 54 )=574 x 3.999=2295.46 million
Therefore, in 2028 the population will be 2295 million
8 | P a g e

Algebra
Solution-4d)
Year 2055 means after = 2028-1974 = 81 years from 1974
Putting the value of x = 81
f (81)=574 (1.026)81
f ( 81 )=574 x 7.999=4590.374 million
f ( 81 )=574 x 7.999=4590.374 million
Therefore, in year 2055 the population will be 4590 million
Solution-4e)
As we can see, the population after 27 years i.e. in 2001 is 2294 million, which is around 4 time
of population in 1974, similarly again after 27 years the population is 4590 million, which is
around 8 time of the population in 1974, It can be concluded that the population of India is
growing 4 times after each 27 years.
Solution-5)
As given in question, 5=logb 32
Log is being defined as
For x > 0, and b > 0, and b ≠ 1
y=logb x is equivalent to by = x
Therefore putting the value place for y = 5 and x =32
We get
b5=32
Ans.
9 | P a g e
Solution-4d)
Year 2055 means after = 2028-1974 = 81 years from 1974
Putting the value of x = 81
f (81)=574 (1.026)81
f ( 81 )=574 x 7.999=4590.374 million
f ( 81 )=574 x 7.999=4590.374 million
Therefore, in year 2055 the population will be 4590 million
Solution-4e)
As we can see, the population after 27 years i.e. in 2001 is 2294 million, which is around 4 time
of population in 1974, similarly again after 27 years the population is 4590 million, which is
around 8 time of the population in 1974, It can be concluded that the population of India is
growing 4 times after each 27 years.
Solution-5)
As given in question, 5=logb 32
Log is being defined as
For x > 0, and b > 0, and b ≠ 1
y=logb x is equivalent to by = x
Therefore putting the value place for y = 5 and x =32
We get
b5=32
Ans.
9 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Algebra
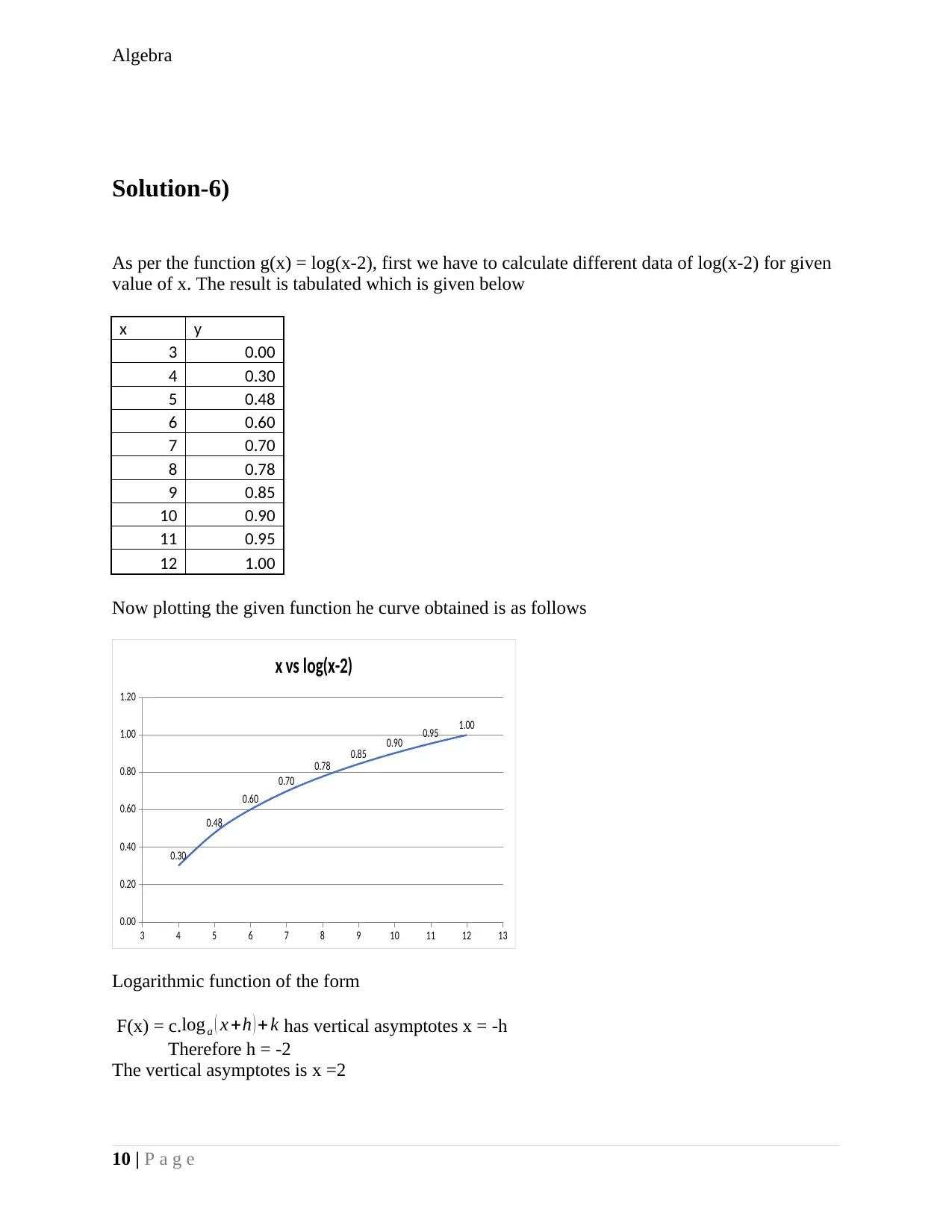
Solution-6)
As per the function g(x) = log(x-2), first we have to calculate different data of log(x-2) for given
value of x. The result is tabulated which is given below
x y
3 0.00
4 0.30
5 0.48
6 0.60
7 0.70
8 0.78
9 0.85
10 0.90
11 0.95
12 1.00
Now plotting the given function he curve obtained is as follows
3 4 5 6 7 8 9 10 11 12 13
0.00
0.20
0.40
0.60
0.80
1.00
1.20
0.30
0.48
0.60
0.70
0.78
0.85 0.90 0.95 1.00
x vs log(x-2)
Logarithmic function of the form
F(x) = c.log a ( x +h ) + k has vertical asymptotes x = -h
Therefore h = -2
The vertical asymptotes is x =2
10 | P a g e
Solution-6)
As per the function g(x) = log(x-2), first we have to calculate different data of log(x-2) for given
value of x. The result is tabulated which is given below
x y
3 0.00
4 0.30
5 0.48
6 0.60
7 0.70
8 0.78
9 0.85
10 0.90
11 0.95
12 1.00
Now plotting the given function he curve obtained is as follows
3 4 5 6 7 8 9 10 11 12 13
0.00
0.20
0.40
0.60
0.80
1.00
1.20
0.30
0.48
0.60
0.70
0.78
0.85 0.90 0.95 1.00
x vs log(x-2)
Logarithmic function of the form
F(x) = c.log a ( x +h ) + k has vertical asymptotes x = -h
Therefore h = -2
The vertical asymptotes is x =2
10 | P a g e
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Algebra
F(x) = c.loga ( x +h ) +k Has no horizontal asymptote
The domain for log(x-2), : [ Solution : x> 2
Interval No tation :(2 , ∞) ] Ans
The Range for log(x-2): [ Solution :−∞<f ( x ) <∞
Interval Notation :(−∞ , ∞) ]
Solution-7)
As given in question,
The function of age percentage for girls is given as
f ( x )=62+ 35 log ( x−4)
Putting the value x = 13 we get
f ( 13 ) =62+35 log (13−4)
f ( 13 )=62+35 log (9)
f ( 13 )=62+35∗0.954243
f ( 13 )=62+33.39849
f ( 13 )=95.39849
F(13) = 95.40 % Ans
Solution-8)
As given in question
f ( t )=88−15 ln ( t +1 ) , 0<t <12
Solution-8a)
The original exam means t =0
f ( 0 )=88−15 ln ( 0+1 )
11 | P a g e
F(x) = c.loga ( x +h ) +k Has no horizontal asymptote
The domain for log(x-2), : [ Solution : x> 2
Interval No tation :(2 , ∞) ] Ans
The Range for log(x-2): [ Solution :−∞<f ( x ) <∞
Interval Notation :(−∞ , ∞) ]
Solution-7)
As given in question,
The function of age percentage for girls is given as
f ( x )=62+ 35 log ( x−4)
Putting the value x = 13 we get
f ( 13 ) =62+35 log (13−4)
f ( 13 )=62+35 log (9)
f ( 13 )=62+35∗0.954243
f ( 13 )=62+33.39849
f ( 13 )=95.39849
F(13) = 95.40 % Ans
Solution-8)
As given in question
f ( t )=88−15 ln ( t +1 ) , 0<t <12
Solution-8a)
The original exam means t =0
f ( 0 )=88−15 ln ( 0+1 )
11 | P a g e

Algebra
f ( 0 )=88−15∗0
f ( 0 )=88
Solution-8b)
After 2 month
f ( 2 ) =88−15 ln ( 2+1 )
f ( 2 ) =88−15 ln ( 2+1 )
f ( 2 ) =88−15 ln ( 3 )
f ( 2 ) =71.52082
After 4 month
f ( 4 )=88−15 ln ( 4+1 )
f ( 4 )=88−15 ln (5 )
f ( 4 )=88−24.1512
f ( 4 ) =63.85843
After 6 month
f ( 6 )=88−15 ln ( 6+1 )
f ( 6 )=88−15 ln ( 7 )
f ( 6 )=88−29.189
f ( 6 )=58.8113
After 8 month
f ( 8 )=88−15 ln ( 8+1 )
12 | P a g e
f ( 0 )=88−15∗0
f ( 0 )=88
Solution-8b)
After 2 month
f ( 2 ) =88−15 ln ( 2+1 )
f ( 2 ) =88−15 ln ( 2+1 )
f ( 2 ) =88−15 ln ( 3 )
f ( 2 ) =71.52082
After 4 month
f ( 4 )=88−15 ln ( 4+1 )
f ( 4 )=88−15 ln (5 )
f ( 4 )=88−24.1512
f ( 4 ) =63.85843
After 6 month
f ( 6 )=88−15 ln ( 6+1 )
f ( 6 )=88−15 ln ( 7 )
f ( 6 )=88−29.189
f ( 6 )=58.8113
After 8 month
f ( 8 )=88−15 ln ( 8+1 )
12 | P a g e
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 22
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.


