Math Homework: Solving Inverse Functions and Logarithmic Equations

This assignment provides detailed solutions to various problems related to inverse functions and logarithmic equations. The solutions cover finding the inverse of different functions, including exponential and polynomial functions, and verifying inverse relationships through composition. The assignment also addresses logarithmic functions, including solving equations using logarithmic properties, the change of base formula, and expanding and contracting logarithmic expressions. Furthermore, the document includes solutions for solving exponential and logarithmic equations, applying logarithms to real-world problems involving compound interest and exponential decay, and determining the time it takes for a quantity to change based on an exponential model. The assignment demonstrates a solid understanding of algebraic concepts and problem-solving techniques.

INVERSE FUNCTIONS
Inverse of the graph ( y=10x ¿
If a function f ( x ) is mapping x ¿ y , thenthe inverse function of f ( x ) maps y back ¿ x
f ( x )=10x ,interchan ging the variables x∧ y , we have :
x=10 y
Thus we solve for y .
Given that f ( x ) =g ( x ) , then ln f ( x ) =ln g ( x )
ln x=ln 10 y
Since log a xb =b∗log a x
ln 10 y= y∗ln10
ln x= y∗ln 10
y= ln x
ln10
Thus the inverse of y=10x is y= ln x
ln 10 .
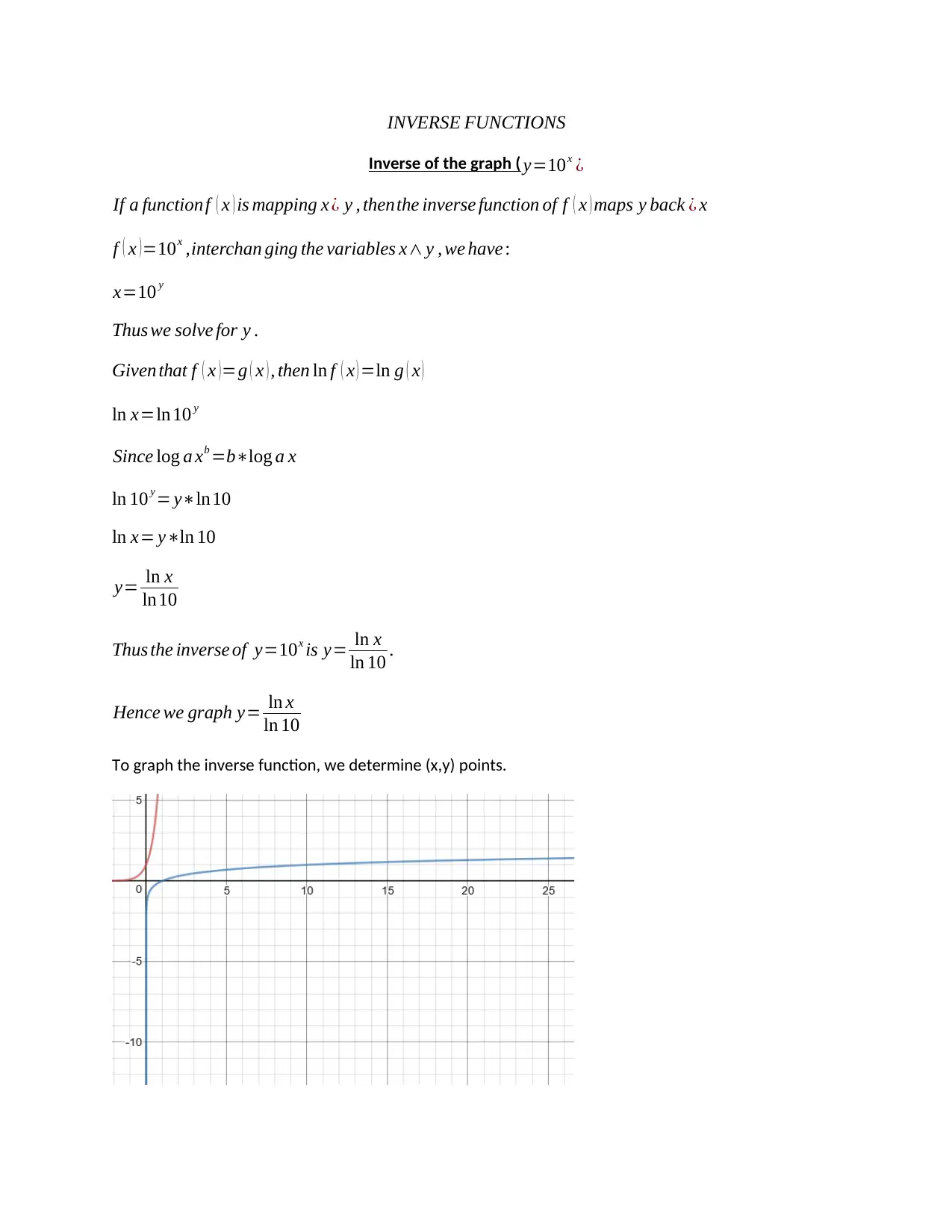
Hence we graph y= ln x
ln 10
To graph the inverse function, we determine (x,y) points.

f−1 ( x ) if f ( x ) =−4 x +9
If a function f ( x ) is mapping x ¿ y , thenthe inverse function of f ( x ) maps y back ¿ x
y=−4 x +9
x=−4 y +9
−4 y +9= x
−4 y +9−9=x−9
−4 y=x−9
−4 y
−4 = x
−4 =−9
−4
y=−x−9
4
f−1 ( x ) =−x−9
4
Inverse of f ( x ) = ( x +1 ) 2−3
Simplifying f ( x ) = ( x+1 )2 −3
f ( x )=x2 +2 x−2
If a function f ( x ) is mapping x ¿ y , thenthe inverse function of f ( x ) maps y back ¿ x
x= y2 +2 y−2
y2 +2 y−2=x Subtracting x ¿ both sides , we have :
y2 +2 y−2−x=x −x
y2 +2 y−2=0
Using quadratic formula with a=1 , b=2, c=−2−x
y= √x +3−1
y=− √x +3−1
Thus Inverse of f ( x ) = ( x +1 ) 2−3 is : y= √ x+ 3−1∧ y=− √ x+ 3−1
Inverse of f ( x )=ln2 x

If a function f ( x ) is mapping x ¿ y , thenthe inverse function of f ( x ) maps y back ¿ x
y=ln 2 x
x=ln 2 y applying logarithmrule : a=log b ¿
x=ln ex
ln (ex ¿)=ln ( 2 y ) Given the logshave the same base : logb f ( x ) =log g b ( x ) ¿
Implying that f ( x ) =g ( x )
For ln ex=ln 2 y ,
we solve ex=2 y
y= ex
2
The inverse of Inverse of f ( x ) =ln 2 x is f ( x ) =e x
2
Inverse of the funct ion4.5 ( x−15 )4 +3 when x ≤15
Applyingbinomial theorem , we have :
( a+b )n=∑
i=0
n
(n
i )an−i bi Where a=x , b=−15
∑
i=0
n
(n
i )an−i bi=∑
i
4
(4
i )x4 −i (−15 )i
4.5 ( x−15 )4 +3=4.5 ∑
i
4
(4
i ) x4−i (−15 )i+3
f ( x )=4.5 x4− 67.5∗24
6 x3 + 1012.5∗24
4 x2−15187.5∗24
6 x+ 227815.5
If a function f ( x ) is mapping x ¿ y , thenthe inverse function of f ( x ) maps y back ¿ x
x=4.5 y 4− 67.5∗24
6 y3 + 1012.5∗24
4 y2− 15187.5∗24
6 y +227815.5
solving for y , we have 45 y4−2700 y3 +60750 y2−607500 y +2278155−x∗10=0

y= 1
3 (45−i2
1
4 √3 ( x−3 )
1
4 ), y= 1
3 (45+i 2
1
4 √3 ( x−3 )
1
4 )
Sinceboth roots are complex , Inverse of the function 4.5 ( x−15 ) 4 +3 when x ≤15 does not exist
Use composition ¿ prove whether the followin g functions are inverses :
If f ( g ( x ) )=g ( f ( x ) ) =x , then f ( x )∧g ( x ) are inverse functions
f ( x )=4 x +1
g ( x ) = x −1
4
f ( g ( x ) )=4 ( x−1
4 )+ 1= 4 x−4
4 =x −1
Hence the functions are not inverses
Use composition ¿ prove whether the follwoing functions areinverses . If they are not , find the inverse of
f ( x)
If f ( g ( x ) )=g ( f ( x ) ) =x , then f ( x )∧g ( x ) are inverse functions
f ( x )= ( x +1 )3−4
g ( x )= ( x−4 )
1
3 −1
f ( g ( x ) ) = [ ( x−4 )
1
3 −1+1 ]
3
−4= [ ( x−4 )
1
3 ]
3
−4
¿ x−4+4=x
Thus f ( g ( x ) )=g ( f ( x ) ) =x hence the functions areinverses
Logarithmic Functions
Question 1
20=4 ( e ) x
ln 20=ln( 4 ( e ) x ¿)=ln 4+ ln ex ¿
ln 20=ln 4 +x∗lne
ln 20=ln 4 +x

8=3x+ 4
ln 8=ln( 3¿¿ x+ 4)¿
44 x=200
ln 44 x=ln200
4 x∗ln 4=ln 200 x= ln200
4∗ln 4
Question 2
log5 20=x
5x=20
ln ( 100 ) =x
ex=100
2∗logx ( 20 )=4
logx 202=4
x4 =202
x4 =400
Question 3
Change of base formula: log b m= log a m
loga b
log3 5
log3 5= loge 5
loge 3 = ln 5
ln 3 =1.465
log6 22
log6 22= loge 22
loge 6 = ln22
ln6 =1.7251
log2 2.9

log2 2.9= loge 2.9
loge 2 = ln 2.9
ln 2 =1.536
Question 4
Product : logb xy=logb x +logb y
Quotient : logb
x
y =logb x −logb y
Power :log b x y= ylo gb x
Expand
a) log 24 ( 3 )
5
log 24 ( 3 )
5 =log 24 + log3−log 5
¿ 4 log 2−log3−log 5
b) log 25
9
log 25
9 =log 25−log 9
¿ log 52−log32
¿ 2 log 5−2 log 3
Contract
c) 6 log3 u+6 log3 v
¿ log3 u6 + log3 v6
¿ log3 u6 v6 =log3 ( uv )6
d) ln x−4 ln y
¿ ln x−ln y 4
¿ ln x
y4
Question 5
Convert to like bases:

a) 42 x +3=16
42 x +3=42
2 x+3=2
2 x=−1
x=−1
2
b) 32 a=3−a +9
2 a=−a+9
3 a=9
a=3
c) 53−2 x =1
53−2 x =50
3−2 x=0
−2 x=−3
x= 3
2
Use logs and log properties to solve:
a) 3b =17
b∗log 3=log 17
b= log17
log 3 =2.5789
b) 4 ( 5t ) −1=15
log 4 ( 5t ) =log ( 15+1 )
log 4+t∗log 5=log 16
t log 5=log 16−log 4
t= log 16−log 4
log5 =0.8614
c) ex−1 −5=5
ex−1=5+5=10
ex−1=10
( x−1 ) ln e=ln 10
x−1=ln 10
x=ln 10+1
x=3.3026
d) −6 (108 n+8 )−3=−23
−6 ( 108n +8 )=−23+3=−20
108 n +8=−20
−6 = 10
3

( 8 n+8 ) log10=log 10
3
8 n+8=
log 10
3
log 10
8 n=
log 10
3
log 10 −8=−7.47712
n=−7.47712
8 =−0.9346
e) a ¿ A=P ( 1+r ) t ,
where A isthe amount ∈the account , P isthe principleamount , r isthe interest rate∧¿
t is the period
b ¿ 2 p= p ( 1.02 ) t
2= ( 1.02 )t
log 2=log (1.02 )t
t= log 2
log 1.02 =35 months
¿ 2 years11 months
f) G=g ( 1.0045 )h
a ¿ Where G isthe numbe r of bacteria colonies after h hrs starting with g colonies
b ¿ 30000=8000 (1.0045 )h
log 30000=¿ log 8000+h log 1.0045 ¿
h= log30000−log 8000
1.0045
¿ 294.3839 hours
Exceeding
a) y=33+ 104 eert , when t=2 , y =120
120=33+104 e2 r
120−33=104 e2 r
87=104 e2 r
log 87=log 104+2 r
2 r=−0.077514086
r =−0.038757
Thus the rate of reduction is 0.038757 Degrees per minute
b) 80=33+104 e−0.038757 t
log 47=log 104±0.038757 t
−0.038757 t=−0.344935481
t=8.89995 ≈ 9

Thuswill take 9 minutes