Algebra Homework: Exploring Quadratic Equations, Functions, and Graphs

This document provides solutions to an algebra homework assignment that focuses on quadratic equations, functions, and their graphical representations. The assignment covers various aspects of quadratic functions, including finding the vertex and axis of symmetry of a parabola, determining the domain and range of a function, and analyzing the behavior of a function. It also includes problems related to the Leading Coefficient Test and the identification of x and y intercepts. Furthermore, the assignment delves into rational functions, asking questions about vertical and horizontal asymptotes, and how to solve them using synthetic division. The solutions are provided in a step-by-step manner, making it easy to understand the concepts and methods involved. The document offers a comprehensive guide to understanding quadratic and rational functions, which is helpful for students studying algebra.

Question One
j ( x )=−x2−1
Question Two
f ( x )=2 x2−8 x +3
Given the parabola y=a ( x−h ) 2+ k ,the vertex isthe coordinate( h , k)
Thus the vertex of the parabolais given by− b
2 a
x=−b
2 a =−−8
2∗2 =2
f ( x )=2 x2−8 x +3=−5
Thus
The vertex is at x = _2____ and y = _-5____
Question Three
a) f ( x )=4−¿
Since the equation is in the form of parabola y=a ( x−h )2 +k , the vertex is
( h , k ) =(1,4)
When x=0 , f ( x )=3
When f ( x )=0 , x=3 ,−1
Thus we have the following points to plot:
( 1,4 ) , ( 0,3 ) , ( 3,0 ) ∧(−1,0)

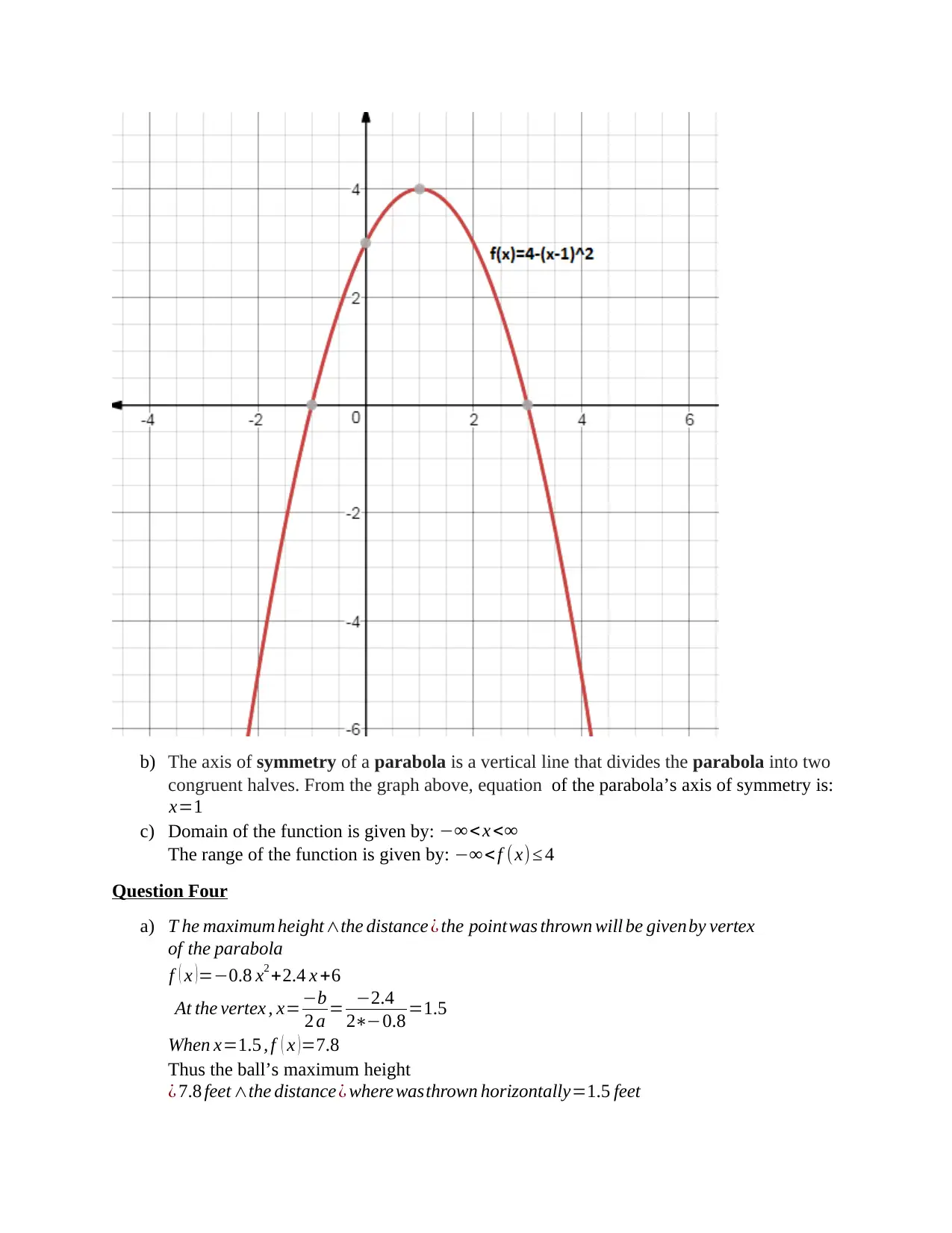
b) The axis of symmetry of a parabola is a vertical line that divides the parabola into two
congruent halves. From the graph above, equation of the parabola’s axis of symmetry is:
x=1
c) Domain of the function is given by: −∞< x <∞
The range of the function is given by: −∞ < f (x) ≤ 4
Question Four
a) T he maximum height∧the distance ¿ the pointwas thrown will be givenby vertex
of the parabola
f ( x ) =−0.8 x2 +2.4 x +6
At the vertex , x=−b
2 a = −2.4
2∗−0.8 =1.5
When x=1.5 , f ( x )=7.8
Thus the ball’s maximum height
¿ 7.8 feet ∧the distance ¿ wherewasthrown horizontally=1.5 feet

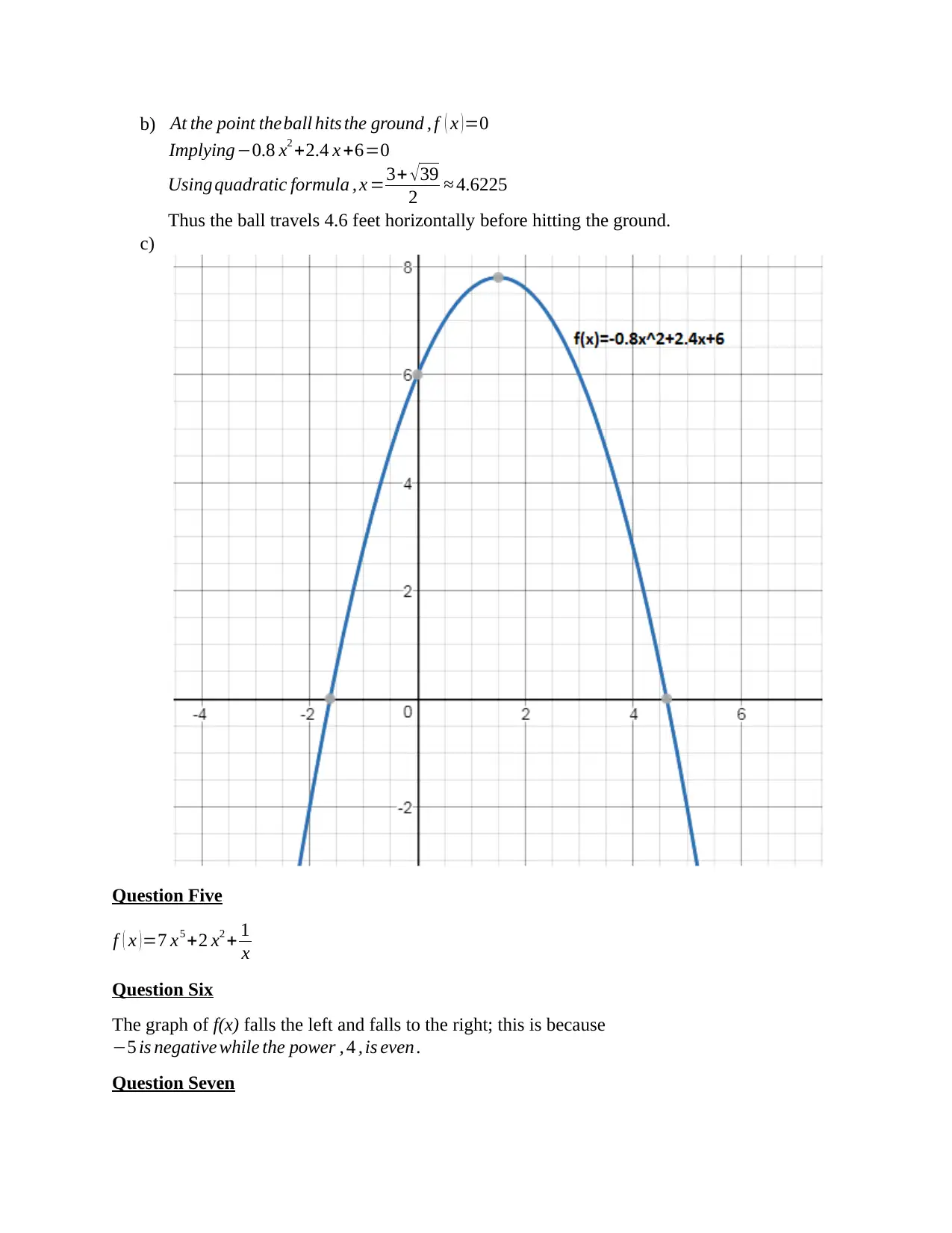
b) At the point theball hits the ground , f ( x )=0
Implying−0.8 x2 +2.4 x +6=0
Using quadratic formula , x =3+ √ 39
2 ≈ 4.6225
Thus the ball travels 4.6 feet horizontally before hitting the ground.
c)
Question Five
f ( x ) =7 x5 +2 x2 + 1
x
Question Six
The graph of f(x) falls the left and falls to the right; this is because
−5 is negative while the power , 4 , is even .
Question Seven

a) The graph of f(x) falls the left and falls to the right; this is because
−1 isnegative while the power , 4 , iseven .
b) At x intecept , f ( x )=0
−x4 + 4 x2=0
−x2 ( x2−4 )=0
x=0 ,
x=± 2
Thus x intercepts are
x=0 ,−2 ,2
The graph crosses both−2∧2 but just touches 0∧turns around .
c) At y intercept, x=0
f ( x )=−x4 +4 x2 When x=0 ,
f ( x )=0
Hence y intercept ¿ 0
d) When a graph is symmetrical about the x-axis, f ( x ) =−f (x )
f ( 1 ) =3
−f ( 1 ) =−3
Thus f ( x ) ≠−f ( x )
Implying the graph is not symmetrical about x axis .
When a graph is symmetrical about y axis, f ( x ) =f (−x )
f ( 1 ) =3
f (−1 )=3
Thus f ( x ) f ( −x ) Implying the graph is symmetrical about y axis
Thus the graph has a y symmetry .
e) Coordinates gathered so far : ( 1,3 ) , ( 0,0 ) , (−2,0 ) , ( 2,0 ) ,(−1,3)

Question Eight
a) f ( x )=0.76 x3 −30 x2−882 x +37807
f ( 40 )=0.76∗403−30∗402−882∗40+37807=3167 ;
This meansthat 40 years after 1970(¿ the year 2010), there were 3167 tigers∈the world .
Thisinformation would be displayed on the graph of f by marking ( 40,3167 ) on the cartesian plane .
b) f ( 40 ) underestimates theactual datashown on the ¯graph .
As per the ¯graph ,∈2010 , there were 3200 tigers ,
Thus the difference=3200=3167=33
Hence f ( 40 ) underestimates by 33 tigers
c) Since 0.76 is positive and the power of x, 3, is odd, the function inclines to the right. If
the efforts to save tigers fail, the information will not be useful in modelling world tiger
population. This is because the information shows that the population is declining while
the Leading Coefficient Test shows that the graph inclines to the right; hence
contradicting each other in the long run.
Question Nine

Divide x4 +2 x3−4 x2 −5 x −6
x2 + x−2 : x4 +2 x3 −4 x2−5 x−6
x2 +x−2
¿ x2+ x3−2 x2−5 x−6
x2+ x−2 ; That is , divide the leading coefficient of the numerator
x4 +2 x3−4 x2−5 x−6∧the divisor x2+x =2: x4
x2 =x2
Quotient=x2
Multiply x2 +x−2 by x2 : x4 +x3−2 x2
Subtract x4 + x3 −2 x2 ¿ x4 + 2 x3−4 x2−5 x−6 ¿ get the new remainder .
Remainder=x3−2 x2−5 x−6
Therefore x4 +2 x3−4 x2−5 x−6
x2 +x−2 =x2 + x3 −2 x2−5 x−6
x2 +x−2
Divide x3−2 x2−5 x−6
x2+ x−2 : x3−2 x2 −5 x −6
x2 + x−2 =x +−3 x2−3 x−6
x2 +x−2
Divide theleading coeffcient pf thenumerator x3−2 x2−6∧thedivisor x2 + x−2 : x3
x2
¿ x
Using the same procedure as done above , get theremainder=−3 x2−3 x−6
Implying x2 + x +−3 x2−3 x−6
x2 +x−2
Divide −3 x2−3 x−6
x2 + x−2 :−3 x2−3 x−6
x2 + x−2 =−3+ −12
x2 + x−12
Quotient=−3 ,
Remainder=−12 ;
Thus x4 +2 x3−4 x2−5 x−6
x2+ x−2 =x2 + x−3− 12
x2 + x−2
Consequently , q ( x )= x2 + x−3∧r ( x )=−12
Question Ten
Write the problem in a division format.

x4 x3 x2 x1 x0
−5 1 −5 1 −5 1
First, write down coefficients without changes
1 −5 1 −5 0
−5 1
Multiply entry in the left part of the table by the last entry in the result row; under the horizontal
line.
Add obtained result to the next coefficient of the dividend and write down the sum
−5 1 −5 1 −5 0
−5
1 −10
Multiply entry in the left part of the table by the last entry in the result row; under the horizontal
line.
Add obtained result to the next coefficient of the dividend and write down the sum.
−5 1 −5 1 −5 0
−5 50
1 −10 51
Multiply entry in the left part of the table by the last entry in the result row; under the horizontal
line
Add obtained result to the next coefficient of the dividend and write down the sum
−5 1 −5 1 −5 1
−5 50 −255
1 −10 51 −260
Multiply entry in the left part of the table by the last entry in the result row; under the horizontal
line.
Add obtained result to the next coefficient of the dividend and write down the sum.
−5 1 −5 1 −5 0
−5 50 −255 1300
1 −10 51 −260 1300

Thus the resulting coefficients are 1 ,−10 , 51 ,−260∧1300
The first four coefficients are part of the quotient while the last coefficient is the remainder.
q ( x )=x3−10 x2 +51 x−260
r ( x ) =1300
Question Eleven
a) For 2 to be a solution to 2 h3 +14 h2 −72, then ( x−2 ) should be a factor of 2 h3 +14 h2−72 .
That is , 2 h3 +14 h2 −72
x−2 , r ( x ) =0
Using synthetic division to get the division coefficients, we have:
2 ,18 ,36 ,∧0
2h3+14 h2−72
h−2 =2 h2 +18 h+36
Thus ( h−2 ) ( 2h2+18 h+36 )=0
( h−2 )=0
h=2
b) Volume of a cuboid=l∗w∗h
¿ h∗2 h∗( h+ 7 ) =72
2 h3 +14 h2 −72=0
( h−2 ) ( 2h2+18 h+36 )=0
( h−2 )=0
h=2
2 h=14 ;h+7=9
Thus the dimension of the box is :
4 inches by 9 inches by 2 inches
Question Twelve
a. As x→ 1+, f(x) → _∞____
b. As x → 1-, f(x) → ___∞ __
c. As x → -2+, f(x) → ___∞__
d. As x → -2-, f(x) → __∞___
e. As x → ∞, f(x) → _0____
f. As x → -∞, f(x) → ____0_

Question thirteen
x−3
x2 −9 = x −3
( x−3)(x +3)
For a rational function, the vertical asymptotes are undefined points (zeros of the denominator),
of the simplified function.
x +3=0; x=−3
x−3=0 ; x=3
Vertical Asymptotes: 3 ,−3
x −3
( x−3)(x +3)
x−3 is a common factor of numerator ∧denominator ,
thus ¿ get a hole , we equatethe factor ¿ zero .
x−3=0
x=3
Holes at x = 3
Hence
Vertical Asymptotes: 3 ,−3
Holes at x = 3
Question fourteen
The degree of the numerator ¿ 2.
The degree of the denominator=2.
Sincethe degrees are equal , the asympote is : numerato r' sleading coefficient
Denominato r' sleading coefficient = 12
3
y=4
Horizontal Asymptote: 4
Question fifteen