Alternating Voltages & Currents Assignment - Access to Engineering

This document presents a comprehensive solution to an electrical engineering assignment focusing on alternating voltages and currents. The solution covers various aspects of AC circuit analysis, including the calculation of amplitude, period, frequency, RMS value, peak-to-peak value, and average value for sinusoidal waveforms. It explains the concepts of phase shift, instantaneous values, and voltage drops across resistors. The assignment also delves into phasor representations of sinusoidal voltages and currents, including the analysis of phase angles and the use of phasor diagrams. The solution includes detailed explanations, calculations, and diagrams to illustrate the concepts. Specific questions address the properties of waveforms, calculations for different functions, voltage drops, phasor representation, and plotting voltages. The document provides a detailed response to each question, offering a thorough understanding of the subject matter.

Question 1
a) Sin(2t+2)-1
F(t)=X*sin(Y(t)+Z) - A
A function in the form shown above is explained as follows
Multiplier X gives the amplitude of the sine wave thus from our question the amplitude is
1 unit
To find the period, ω (omega) of the sine waveform, Y is used as shown in the formula
below
ω=period of regular sine wave/|Y|, but period of regular sine wave is 2*∏
= 2*∏/2
= ∏
Z/Y from the equation gives the phase shift of the function, from our question the sine
wave is shifted to the left (due to positive sign that comes before Z) by one unit. A on the
other hand indicates the vertical shift of the waveform, negative sign before A represent
downward shift and a positive sign upward shift, thus the function in question was shifted
downwards by 1 unit
To find the frequency, F of a function
F=1/period, period was found to be ∏
=1/∏ hertz
RMS, instantaneous, peak to peak and average value is cleared demonstrated by Figure 1:
Figure 1: properties of a waveform
Instantaneous value of the function = Vmax*sin (ω) t, omega was found to be ∏,
thus

=1*sin (∏) t, where Vmax is the amplitude
RMS value of the function= peak voltage*1/ , peak value is 1 from the function
= 1*0.707
= 0.707 units
Peak to peak value is 2 units, one unit above reference axis and one unit below
Average value of the function = peak value* 0.637
= 1*0.637
= 0.637 units
b) Function 2 sin 5 t
F(t)= X sin Y (t)
X= 2, it represents the amplitude of the waveform
Y= 5, used to compute period of the waveform
Period, ω of the waveform is given by
ω=regular period of a sine function/Y
=2*∏/5= 2/5*∏
Frequency of the function is calculated from the period by the relation below
F= 1/period = 1 / (2∏/5) = 5/2∏
Instantaneous value of the sine function is
Vi= Vmax*sin ω t, from above computation Vmax is equal to the amplitude and
ω=2/5∏
Vi= 2*sin (2∏/5) t
Peak to peak value is 4 units, 2 units above reference axis and 2 units below
RMS value is given by peak value multiplied by 1/
Peak value of the function from figure 1 is given by 2 units
RMS value=peak value * 0.707
= 2*0.707
=1.414 units
Average value is computed by multiplying peak value by 0.637
Average value= 2*0.637
= 1.274 units

Question 2
Amplitude is the measure of maximum displacement of a wave from its point of equilibrium.
Period is the time taken to complete one cycle.
Frequency is the measure of cycles of a wave in a second.
Peak-to-peak is the measure of the displacement from top crest to the bottom crest. It is also
equivalent to twice the amplitude.
Instantaneous value of an alternating waveform is the value of the wave at a particular instant.
The average value of a sinusoidal quantity is the average of half a cycle and is calculated by
multiplying peak value by a factor of 0.637.
The RMS value of a wave is the effective value of an alternating waveform and is equivalent to
peak value multiplied by 0.707
Question 3
Resistor value is 47 ohms and a 50 V source supply
Instantaneous value of the voltage source, e is given by the equation
e=Ep*sin ω (t)
Ep is the peak value of the voltage in volts,
ω is the angular velocity in radians
Ep= E rms* , E rms is the RMS value of the voltage and is provided in the question
= 50 *
=70.71 volts
Instantaneous value of the voltage source
e=70.71*sin ω t
voltage drop across the resistor is equal the voltage of source, thus a voltage drop across the
resistor is given by

e=70.71*sin ω t
amplitude of voltage drop is given by 70.71 volts from the equation above
period of the waveform is ω= 2*∏*f = 2* *60=377
frequency is equal to that of the source and is assumed to be 60 Hz
peak to peak value of the voltage drop is given by 2*70.71=141.42 volts
instantaneous value of the voltage drop is given by
Vi=Vmax*sin ω t
= 70.71*sin (377) t
RMS value of the voltage drop is given by peak value multiplied by 1/
RMS value= 70.71*0.707
= 50 volts
Average value of the voltage drop is given by
Average value=peak voltage*0.637
= 45.04 volts
Question 4
Phasor representation of two sinusoidal voltages

On phasor diagrams, the phasors rotate in an anticlockwise direction. Voltage A lies on the
horizontal axis as its phase angle is zero. Hence voltage B is leading voltage A.
Question 5
Figure 2: phasors of currents A and B
The lengths of phasors in the diagram above is directly proportional to the magnitude of the
current elements.
Current B is lagging current A by a value of 20 degrees. The phasors are rotating in an
anticlockwise direction as shown by the arrow in the figure 2. In its rotation, phasor of current B
lags behind that of current A.
Question 6
Phasors of voltages A and B are represented by figure 3, the lengths of each phasor is directly
proportional to the magnitude of sinusoidal voltages, the diagram is drawn to scale, voltage A
(Sin ω t) is taken at the reference, the angle between phasor A and B represents the phase shift
between the two waveforms and is given by 50 degrees. Using parallelogram properties
diagonal as is drawn as is shown in the figure below, the length of the diagonal will give the
resultant magnitude of the added voltages, angle between the diagonal and the reference axis
gives the phase shift of the resultant waveform.

Figure 3; addition phasors
A+B=5.8*Sin (ωt+45)
Question 7
Phasors of voltages A and B are represented by figure 4, the lengths of each phasor is directly
proportional to the magnitude of sinusoidal voltages, the diagram is drawn to scale, voltage A (-
7Sin(2ω t-15) is taken as the reference axis, the angle between phasor A and B represents the
phase shift between the two waveforms and is given by 15+50=65 degrees. Using parallelogram
properties diagonal as is drawn as is shown in the figure below, the length of the diagonal will
give the resultant magnitude of the added voltages, angle between the diagonal and the reference
axis gives the phase shift of the resultant waveform.

A+B=20*Sin (2ωt+30)
Question 8
Plotting voltages
Voltage A
A= 10 Sin(2x+10) and can be written as a A=10 Sin (x+5)
10 is the magnitude of the waveform and represents the amplitude of the waveform
5 represents phase shift
Voltage B
B= 5 Sin (x+3)+1
5 represent the amplitude of waveform
3 represents 3 degrees phase shift to the left
1 represents vertical shift that is waveform is shifted by 1 unit upwards.
Voltages A and B are plotted as shown in figure 5. Voltage B drawn in blue pen and A pencil

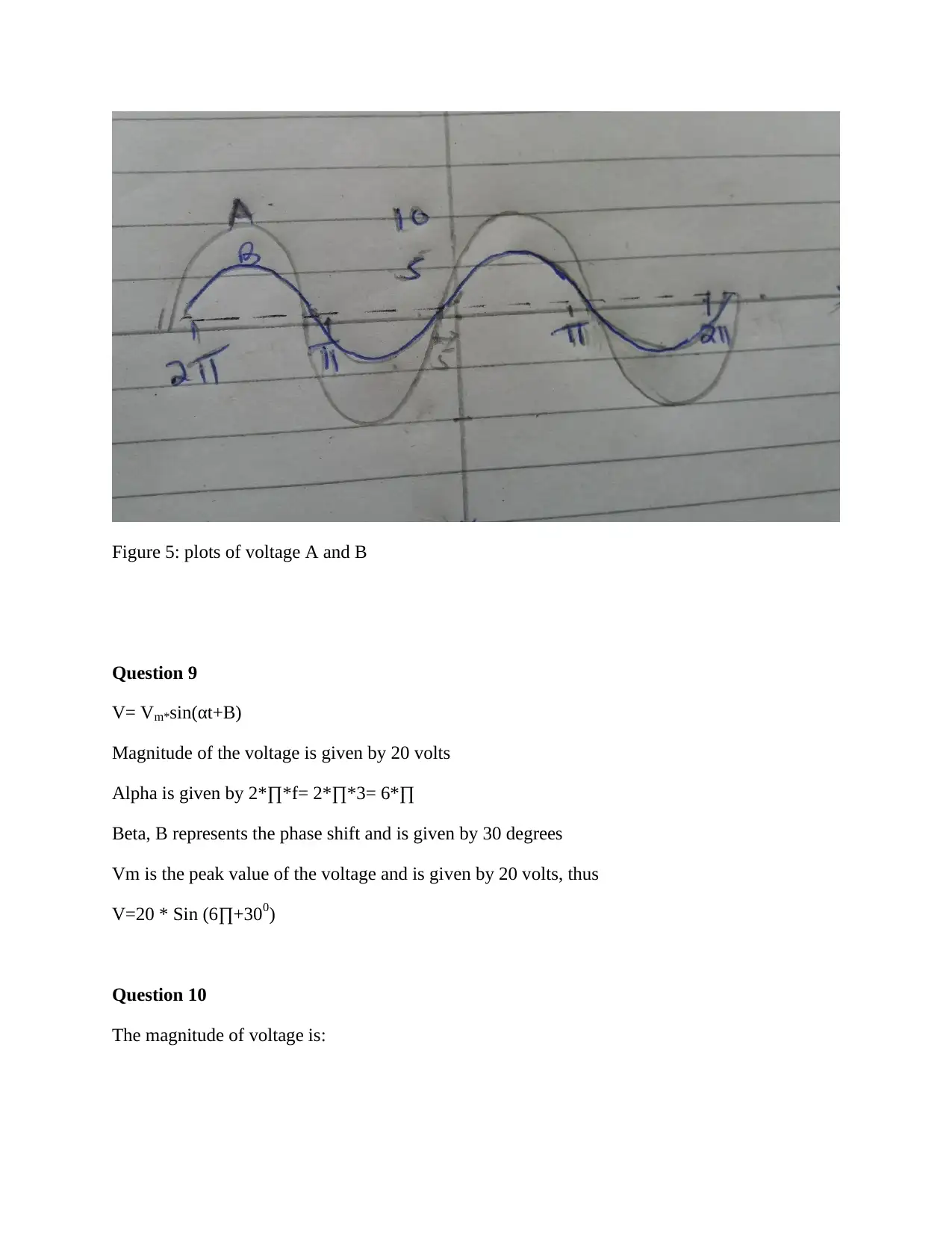
Figure 5: plots of voltage A and B
Question 9
V= Vm*sin(αt+B)
Magnitude of the voltage is given by 20 volts
Alpha is given by 2*∏*f= 2*∏*3= 6*∏
Beta, B represents the phase shift and is given by 30 degrees
Vm is the peak value of the voltage and is given by 20 volts, thus
V=20 * Sin (6∏+300)
Question 10
The magnitude of voltage is:

Frequency is 60Hz hence:
α
α
The phase is:
Hence
Question 11
From ohms law V=I*R
Voltage of the source is given by
V=V max*Sin ω t
Voltage drop across the resistor is equal voltage at the source, thus
VR=V=Vmax*Sin ω t
Instantaneous current through the resistor from ohms law is given by
IR=VR/R=Vmax*Sin ω t/R, But V/R=I, Thus
=Imax*Sin ω t, since Vmax/R=Imax
Question 12
The voltage is expressed as:
V = Sin(αt+ )

where:
the magnitude of voltage is
= 150
and
α where T=6s
α
and phase angle is
=0
Thus voltage is equivalent to:
V= 150 Sin( ) = 150
Current through the resistor:
I=150/47= 3.19A
Power consumed by resistor:
P= = = 478.28W
Question thirteen
Resistor is connected to ac supply of A=10<50
From ohms law IR=VR/R
Voltage drop across the resistor VR is equal to the voltage of the source, thus
VR=10*Sin ω t

Instantaneous current IR is thus given by
IR=VR/R=10* Sin ω t/47=0.213*Sin ω t
Power consumed by the resistor is given by the formula
P= IR2*R, Where R is the resistance of the resistor is given by 47 ohms
=0.2132*47
=2.132 watts
Question 14
a) Instanteneous voltage and current
Frequency = 30Hz
ω = = = 188.5
ω
b) AC voltage and current waveforms
This circuit has a purely resistive impedance hence current and voltage are in phase.

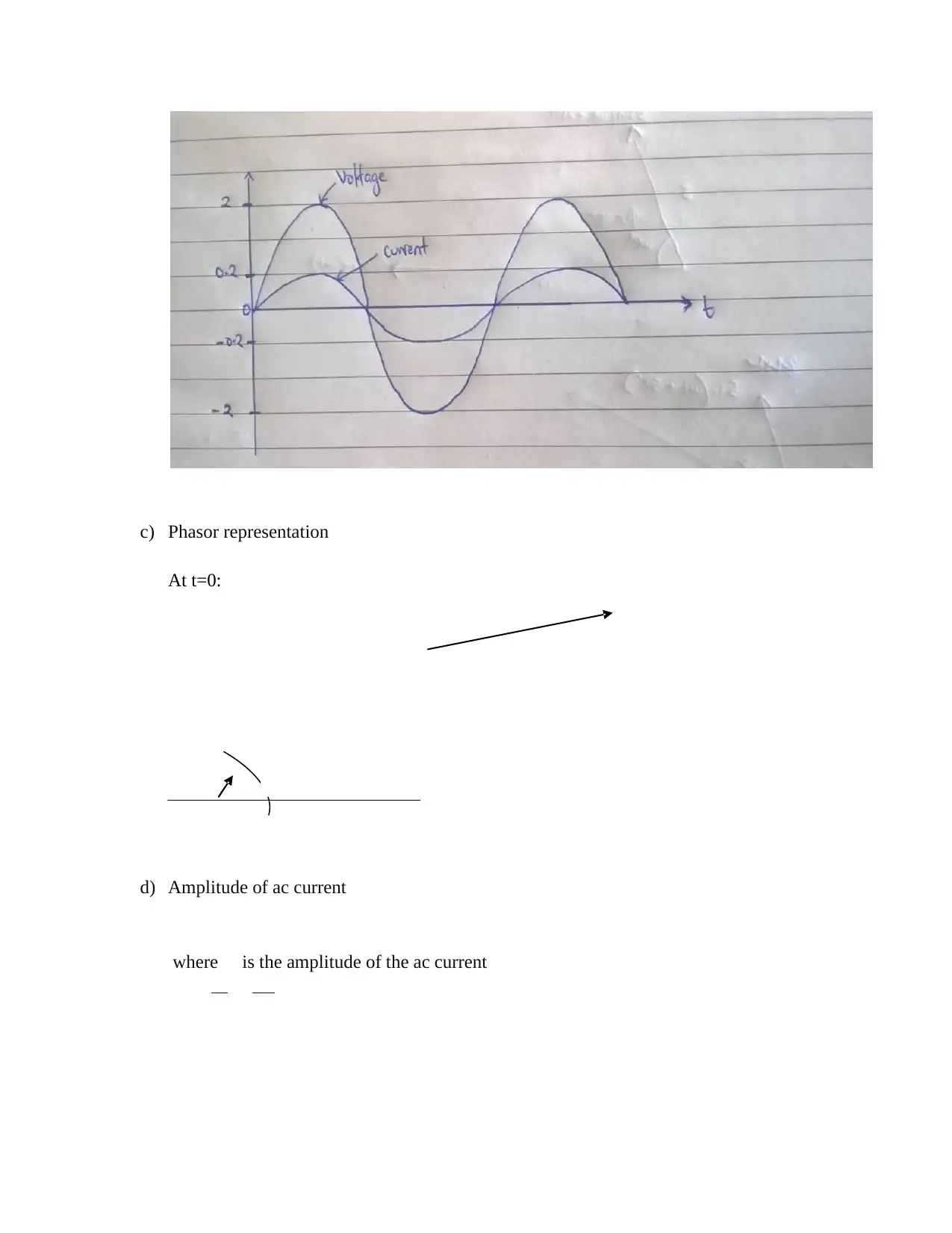
c) Phasor representation
At t=0:
d) Amplitude of ac current
where is the amplitude of the ac current

References
ElectronicsTutorials. n.d, Phasors Diagrams and Phasor Algebra, Retrieved from
https://www.electronics-tutorials.ws/accircuits/phasors.html
PURPLEMATH.n.d, Graphing Trigonometric Functions, Retrieved from
https://www.purplemath.com/modules/grphtrig2.htm