University Circuits Lab: Passive Frequency Selective Circuit Portfolio
VerifiedAdded on 2022/08/25
|16
|912
|15
Practical Assignment
AI Summary
This document presents a solution for a practical assignment focused on the analysis and design of passive frequency selective circuits, specifically RC and LC low-pass filters. The assignment involves deriving the two-port network representation of these circuits, calculating key parameters such as cutoff frequency, and analyzing their behavior at different frequencies. The solution includes circuit diagrams implemented in LTSpice, along with tables of circuit parameters and magnitude/phase plots. The student derives transfer functions, calculates slopes, and determines fractional percentage errors. The document also includes discussions on the simulation parameters and their deviations from calculated values, providing a comprehensive overview of the filter design and analysis process. The assignment assesses the students' ability to apply theoretical knowledge to practical circuit design problems.

1
Passive Frequency Selective Circuits
Student’s Name
Institutional Affiliation
Date
Passive Frequency Selective Circuits
Student’s Name
Institutional Affiliation
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

2
Passive RC Low Pass Filter
The input impedance of the oscilloscope is usually large (¿ 1 M Ω) to avoid loading the circuit
it is connected to. The impedance of the source, on the other hand, is usually low in the order
of50 Ω.
Rs=50 Ω
RL=1 M Ω
f c=1 kHz
Since the input impedance of the oscilloscope is much larger than the impedance of the
capacitor, the parallel combination of the two impedances will be just the impedance of the
capacitor. Therefore, the impedance of the oscilloscope may be neglected.
The cutoff frequency ωc is given by,
ωc= 1
RC
Taking into account the output resistance of the generatorRs, the frequency becomes,
Passive RC Low Pass Filter
The input impedance of the oscilloscope is usually large (¿ 1 M Ω) to avoid loading the circuit
it is connected to. The impedance of the source, on the other hand, is usually low in the order
of50 Ω.
Rs=50 Ω
RL=1 M Ω
f c=1 kHz
Since the input impedance of the oscilloscope is much larger than the impedance of the
capacitor, the parallel combination of the two impedances will be just the impedance of the
capacitor. Therefore, the impedance of the oscilloscope may be neglected.
The cutoff frequency ωc is given by,
ωc= 1
RC
Taking into account the output resistance of the generatorRs, the frequency becomes,

3
ωc= 1
( R+ Rs) C
2 π ( 1000 ) = 1
( R+ Rs ) C
If we choose a value of the capacitor as47 nF, the resistances are given by,
( R+Rs )= 1
( 2 π ( 1000 ) ) ( 47 ×10−9 )
( R+ Rs )=3386.28
But Rs=50, therefore,
R=3386.28−50=3336.28Ω
The closest practical resistor value is,
R=3.3 k
Figure 1: Circuit implemented in LTSpice
ωc= 1
( R+ Rs) C
2 π ( 1000 ) = 1
( R+ Rs ) C
If we choose a value of the capacitor as47 nF, the resistances are given by,
( R+Rs )= 1
( 2 π ( 1000 ) ) ( 47 ×10−9 )
( R+ Rs )=3386.28
But Rs=50, therefore,
R=3386.28−50=3336.28Ω
The closest practical resistor value is,
R=3.3 k
Figure 1: Circuit implemented in LTSpice
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
4
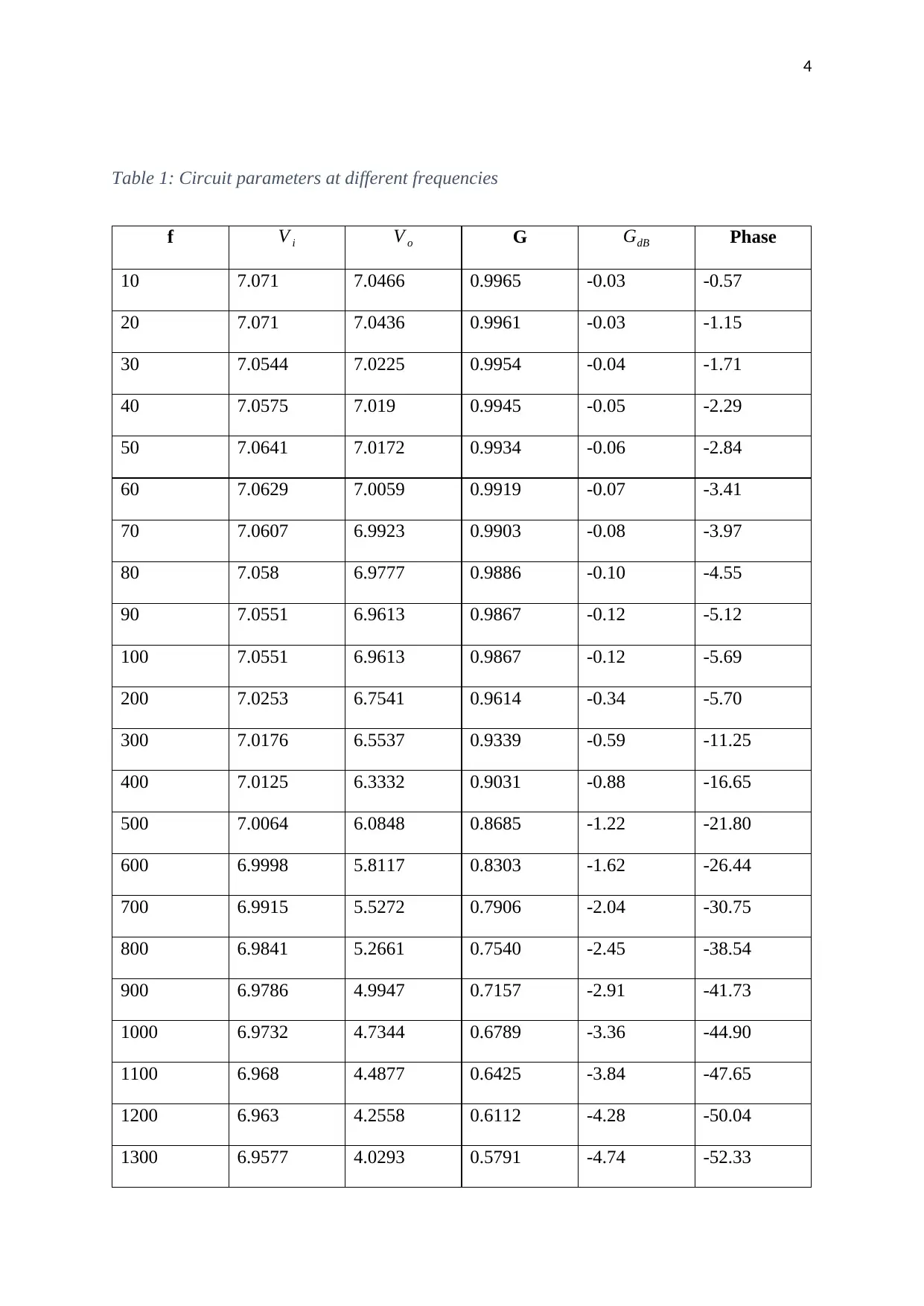
Table 1: Circuit parameters at different frequencies
f V i V o G GdB Phase
10 7.071 7.0466 0.9965 -0.03 -0.57
20 7.071 7.0436 0.9961 -0.03 -1.15
30 7.0544 7.0225 0.9954 -0.04 -1.71
40 7.0575 7.019 0.9945 -0.05 -2.29
50 7.0641 7.0172 0.9934 -0.06 -2.84
60 7.0629 7.0059 0.9919 -0.07 -3.41
70 7.0607 6.9923 0.9903 -0.08 -3.97
80 7.058 6.9777 0.9886 -0.10 -4.55
90 7.0551 6.9613 0.9867 -0.12 -5.12
100 7.0551 6.9613 0.9867 -0.12 -5.69
200 7.0253 6.7541 0.9614 -0.34 -5.70
300 7.0176 6.5537 0.9339 -0.59 -11.25
400 7.0125 6.3332 0.9031 -0.88 -16.65
500 7.0064 6.0848 0.8685 -1.22 -21.80
600 6.9998 5.8117 0.8303 -1.62 -26.44
700 6.9915 5.5272 0.7906 -2.04 -30.75
800 6.9841 5.2661 0.7540 -2.45 -38.54
900 6.9786 4.9947 0.7157 -2.91 -41.73
1000 6.9732 4.7344 0.6789 -3.36 -44.90
1100 6.968 4.4877 0.6425 -3.84 -47.65
1200 6.963 4.2558 0.6112 -4.28 -50.04
1300 6.9577 4.0293 0.5791 -4.74 -52.33
Table 1: Circuit parameters at different frequencies
f V i V o G GdB Phase
10 7.071 7.0466 0.9965 -0.03 -0.57
20 7.071 7.0436 0.9961 -0.03 -1.15
30 7.0544 7.0225 0.9954 -0.04 -1.71
40 7.0575 7.019 0.9945 -0.05 -2.29
50 7.0641 7.0172 0.9934 -0.06 -2.84
60 7.0629 7.0059 0.9919 -0.07 -3.41
70 7.0607 6.9923 0.9903 -0.08 -3.97
80 7.058 6.9777 0.9886 -0.10 -4.55
90 7.0551 6.9613 0.9867 -0.12 -5.12
100 7.0551 6.9613 0.9867 -0.12 -5.69
200 7.0253 6.7541 0.9614 -0.34 -5.70
300 7.0176 6.5537 0.9339 -0.59 -11.25
400 7.0125 6.3332 0.9031 -0.88 -16.65
500 7.0064 6.0848 0.8685 -1.22 -21.80
600 6.9998 5.8117 0.8303 -1.62 -26.44
700 6.9915 5.5272 0.7906 -2.04 -30.75
800 6.9841 5.2661 0.7540 -2.45 -38.54
900 6.9786 4.9947 0.7157 -2.91 -41.73
1000 6.9732 4.7344 0.6789 -3.36 -44.90
1100 6.968 4.4877 0.6425 -3.84 -47.65
1200 6.963 4.2558 0.6112 -4.28 -50.04
1300 6.9577 4.0293 0.5791 -4.74 -52.33
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5
1400 6.9523 3.8057 0.5474 -5.23 -54.21
1500 6.9489 3.6166 0.5205 -5.67 -56.22
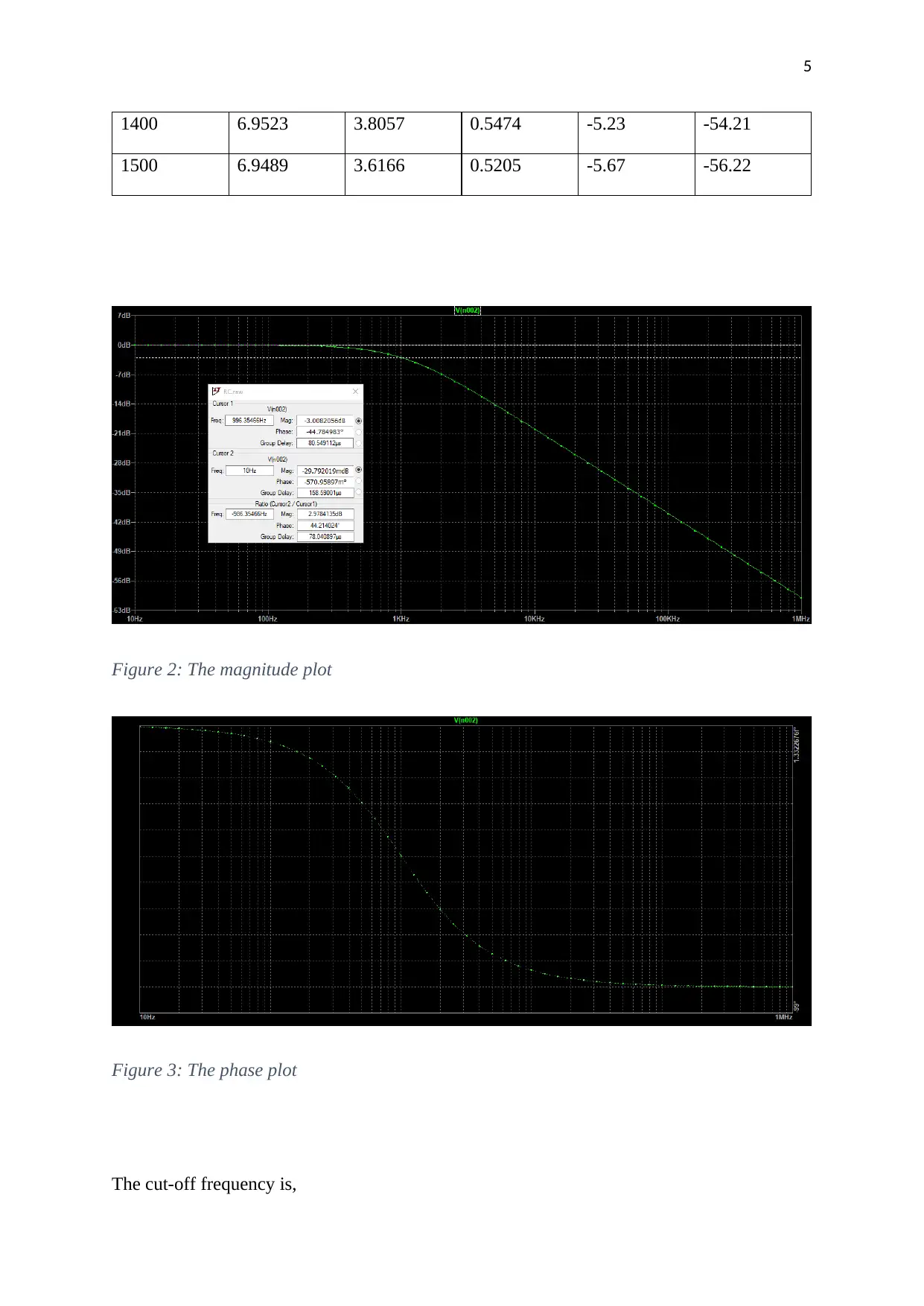
Figure 2: The magnitude plot
Figure 3: The phase plot
The cut-off frequency is,
1400 6.9523 3.8057 0.5474 -5.23 -54.21
1500 6.9489 3.6166 0.5205 -5.67 -56.22
Figure 2: The magnitude plot
Figure 3: The phase plot
The cut-off frequency is,

6
f c
actual=996.35 Hz
The per decade slope of the magnitude curve is,
Sdecade
actual =−19.94 dB/decade
The per octave slope of the magnitude curve is,
Soctave
actual =5.99 dB/octave
The passband phase is,
θpass
actual=ranges ¿ 0 ¿ about−44.15 °
f c
actual=996.35 Hz
The per decade slope of the magnitude curve is,
Sdecade
actual =−19.94 dB/decade
The per octave slope of the magnitude curve is,
Soctave
actual =5.99 dB/octave
The passband phase is,
θpass
actual=ranges ¿ 0 ¿ about−44.15 °
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

7
The stopband phase is,
θstop
actual=ranges ¿−44.15 °¿ about 89.9°
The phase at the cutoff frequency is,
θactual
cutoff =−44.15°
The fractional percentage error between the cutoff frequency value and the one specified in
the design is,
Ef = 1000−996.35
1000 ×100 %=0.365 %
Deriving the transfer function for the circuit,
The reactance of the capacitor is,
X c=− jωC = 1
jωC
The capacitor is in parallel with the load RL
RL/¿ 1
jωC =
RL × 1
jωC
RL+ 1
jωC
=
RL
jωC
jωC RL+ 1
jωC
= RL
jωC RL+1
Since the output voltage is obtained across the parallel combination of the capacitor and the
load resistor, the transfer function is given by,
H ( jω ) =
RL /¿ 1
jωC
RL/¿ 1
jωC +R+ Rs
=
RL /¿ 1
jωC
RL/¿ 1
jωC + Re
, w h ere Re=R + Rs
The stopband phase is,
θstop
actual=ranges ¿−44.15 °¿ about 89.9°
The phase at the cutoff frequency is,
θactual
cutoff =−44.15°
The fractional percentage error between the cutoff frequency value and the one specified in
the design is,
Ef = 1000−996.35
1000 ×100 %=0.365 %
Deriving the transfer function for the circuit,
The reactance of the capacitor is,
X c=− jωC = 1
jωC
The capacitor is in parallel with the load RL
RL/¿ 1
jωC =
RL × 1
jωC
RL+ 1
jωC
=
RL
jωC
jωC RL+ 1
jωC
= RL
jωC RL+1
Since the output voltage is obtained across the parallel combination of the capacitor and the
load resistor, the transfer function is given by,
H ( jω ) =
RL /¿ 1
jωC
RL/¿ 1
jωC +R+ Rs
=
RL /¿ 1
jωC
RL/¿ 1
jωC + Re
, w h ere Re=R + Rs
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
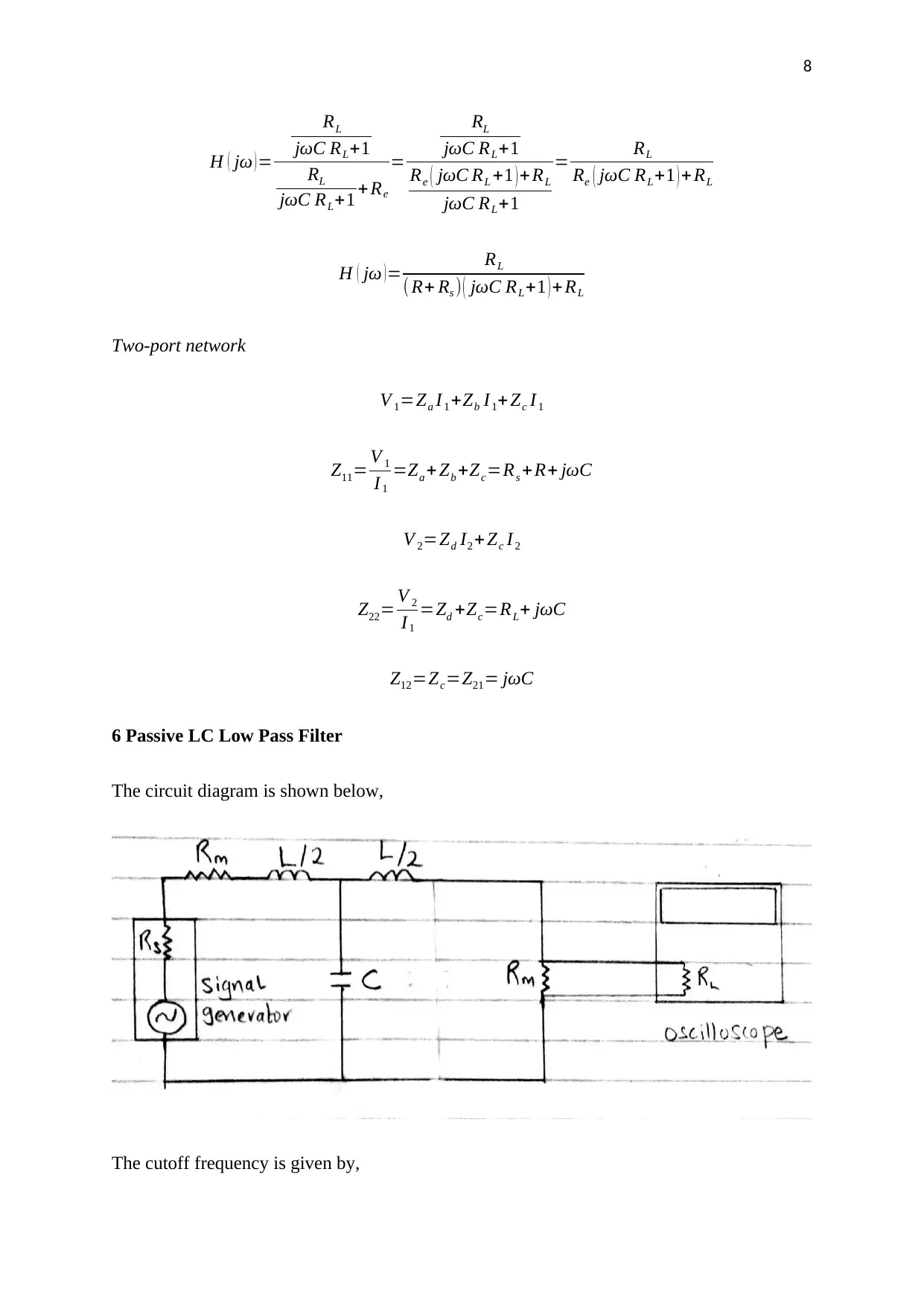
H ( jω ) =
RL
jωC RL+1
RL
jωC RL+1 +Re
=
RL
jωC RL+1
Re ( jωC RL +1 ) +RL
jωC RL+1
= RL
Re ( jωC RL+1 ) + RL
H ( jω )= RL
( R+ Rs ) ( jωC RL+1 ) + RL
Two-port network
V 1=Za I1 +Zb I1+ Zc I 1
Z11= V 1
I 1
=Za + Zb +Zc=Rs + R+ jωC
V 2=Zd I2 + Zc I 2
Z22= V 2
I1
=Zd +Zc=RL+ jωC
Z12=Zc=Z21= jωC
6 Passive LC Low Pass Filter
The circuit diagram is shown below,
The cutoff frequency is given by,
H ( jω ) =
RL
jωC RL+1
RL
jωC RL+1 +Re
=
RL
jωC RL+1
Re ( jωC RL +1 ) +RL
jωC RL+1
= RL
Re ( jωC RL+1 ) + RL
H ( jω )= RL
( R+ Rs ) ( jωC RL+1 ) + RL
Two-port network
V 1=Za I1 +Zb I1+ Zc I 1
Z11= V 1
I 1
=Za + Zb +Zc=Rs + R+ jωC
V 2=Zd I2 + Zc I 2
Z22= V 2
I1
=Zd +Zc=RL+ jωC
Z12=Zc=Z21= jωC
6 Passive LC Low Pass Filter
The circuit diagram is shown below,
The cutoff frequency is given by,

9
f c= 1
π √ LC
f c
2= 1
( π ) 2 LC
( πf )2= 1
LC
L= 1
( πf ) 2 C
Let C=1 μF
L= 1
(π2 )(10002 )(1×10−6 )
¿ 0.1013 H
L=101.3 mH
L
2 =50.65 mH
The available practical component values are,
L=51 mH
C=1 μF
Matching the filter
Z0=π f c L∨Z0 = 1
π f c C
Z0= ( π ) ( 1000 ) ( 50.65 ) =159.12Ω
The matching load resistance is therefore 159.12Ω
The matching input impedance becomes,
f c= 1
π √ LC
f c
2= 1
( π ) 2 LC
( πf )2= 1
LC
L= 1
( πf ) 2 C
Let C=1 μF
L= 1
(π2 )(10002 )(1×10−6 )
¿ 0.1013 H
L=101.3 mH
L
2 =50.65 mH
The available practical component values are,
L=51 mH
C=1 μF
Matching the filter
Z0=π f c L∨Z0 = 1
π f c C
Z0= ( π ) ( 1000 ) ( 50.65 ) =159.12Ω
The matching load resistance is therefore 159.12Ω
The matching input impedance becomes,
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

10
159.12−Rs=159.12−50=109.12Ω
Closest actual resistor values are,
R=100Ω
R=150Ω
Figure 4: Circuit implemented in LTSpice
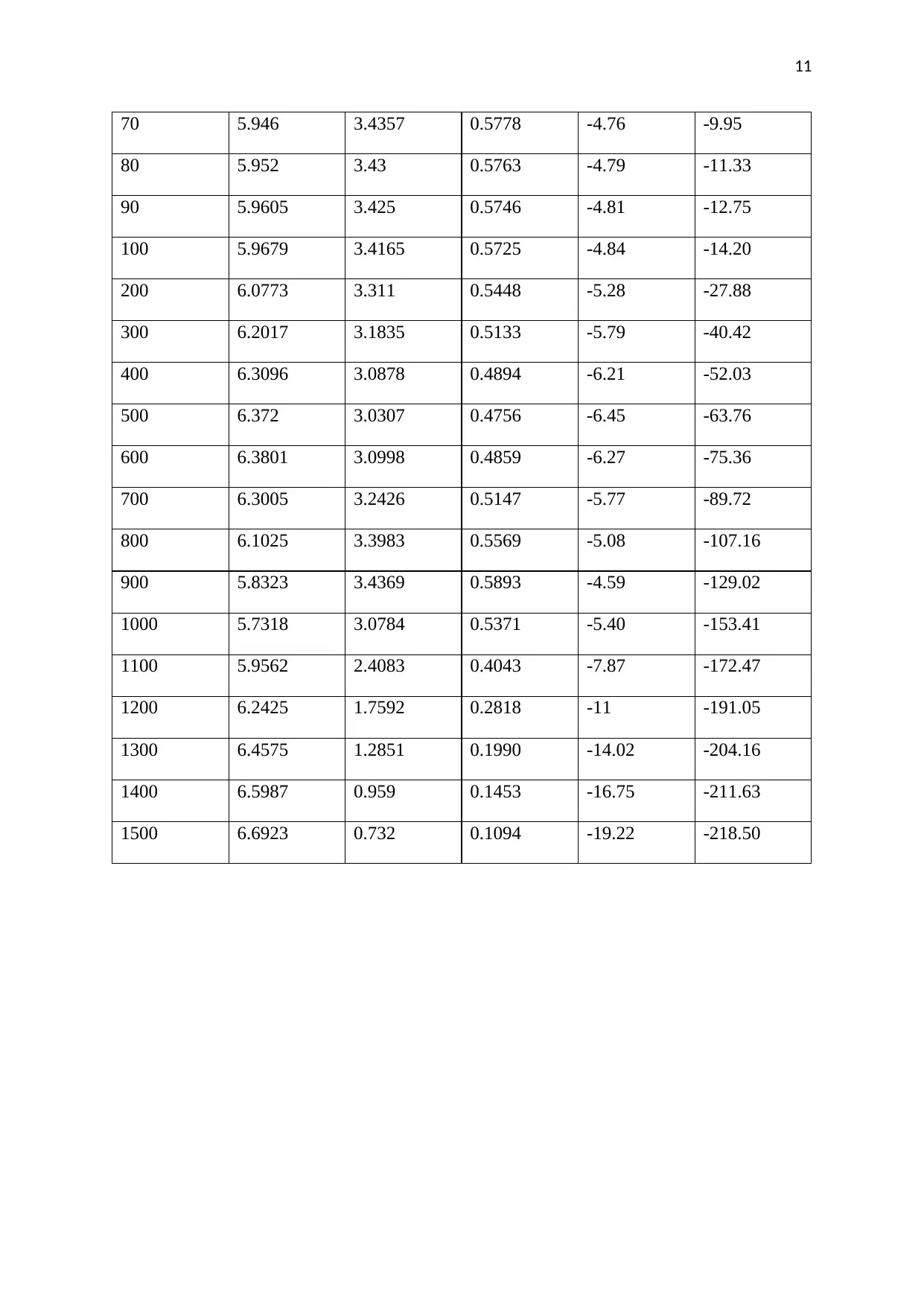
Table 2: Circuit parameters at different frequencies
f V i V o G GdB Phase
10 5.953 3.5273 0.5925 -4.55 -1.43
20 5.9546 3.5168 0.5906 -4.57 -2.85
30 5.9493 3.4979 0.5880 -4.61 -4.31
40 5.944 3.4776 0.5851 -4.66 -5.72
50 5.9424 3.4612 0.5825 -4.69 -7.11
60 5.9423 3.4465 0.5800 -4.73 -8.55
159.12−Rs=159.12−50=109.12Ω
Closest actual resistor values are,
R=100Ω
R=150Ω
Figure 4: Circuit implemented in LTSpice
Table 2: Circuit parameters at different frequencies
f V i V o G GdB Phase
10 5.953 3.5273 0.5925 -4.55 -1.43
20 5.9546 3.5168 0.5906 -4.57 -2.85
30 5.9493 3.4979 0.5880 -4.61 -4.31
40 5.944 3.4776 0.5851 -4.66 -5.72
50 5.9424 3.4612 0.5825 -4.69 -7.11
60 5.9423 3.4465 0.5800 -4.73 -8.55
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
11
70 5.946 3.4357 0.5778 -4.76 -9.95
80 5.952 3.43 0.5763 -4.79 -11.33
90 5.9605 3.425 0.5746 -4.81 -12.75
100 5.9679 3.4165 0.5725 -4.84 -14.20
200 6.0773 3.311 0.5448 -5.28 -27.88
300 6.2017 3.1835 0.5133 -5.79 -40.42
400 6.3096 3.0878 0.4894 -6.21 -52.03
500 6.372 3.0307 0.4756 -6.45 -63.76
600 6.3801 3.0998 0.4859 -6.27 -75.36
700 6.3005 3.2426 0.5147 -5.77 -89.72
800 6.1025 3.3983 0.5569 -5.08 -107.16
900 5.8323 3.4369 0.5893 -4.59 -129.02
1000 5.7318 3.0784 0.5371 -5.40 -153.41
1100 5.9562 2.4083 0.4043 -7.87 -172.47
1200 6.2425 1.7592 0.2818 -11 -191.05
1300 6.4575 1.2851 0.1990 -14.02 -204.16
1400 6.5987 0.959 0.1453 -16.75 -211.63
1500 6.6923 0.732 0.1094 -19.22 -218.50
70 5.946 3.4357 0.5778 -4.76 -9.95
80 5.952 3.43 0.5763 -4.79 -11.33
90 5.9605 3.425 0.5746 -4.81 -12.75
100 5.9679 3.4165 0.5725 -4.84 -14.20
200 6.0773 3.311 0.5448 -5.28 -27.88
300 6.2017 3.1835 0.5133 -5.79 -40.42
400 6.3096 3.0878 0.4894 -6.21 -52.03
500 6.372 3.0307 0.4756 -6.45 -63.76
600 6.3801 3.0998 0.4859 -6.27 -75.36
700 6.3005 3.2426 0.5147 -5.77 -89.72
800 6.1025 3.3983 0.5569 -5.08 -107.16
900 5.8323 3.4369 0.5893 -4.59 -129.02
1000 5.7318 3.0784 0.5371 -5.40 -153.41
1100 5.9562 2.4083 0.4043 -7.87 -172.47
1200 6.2425 1.7592 0.2818 -11 -191.05
1300 6.4575 1.2851 0.1990 -14.02 -204.16
1400 6.5987 0.959 0.1453 -16.75 -211.63
1500 6.6923 0.732 0.1094 -19.22 -218.50
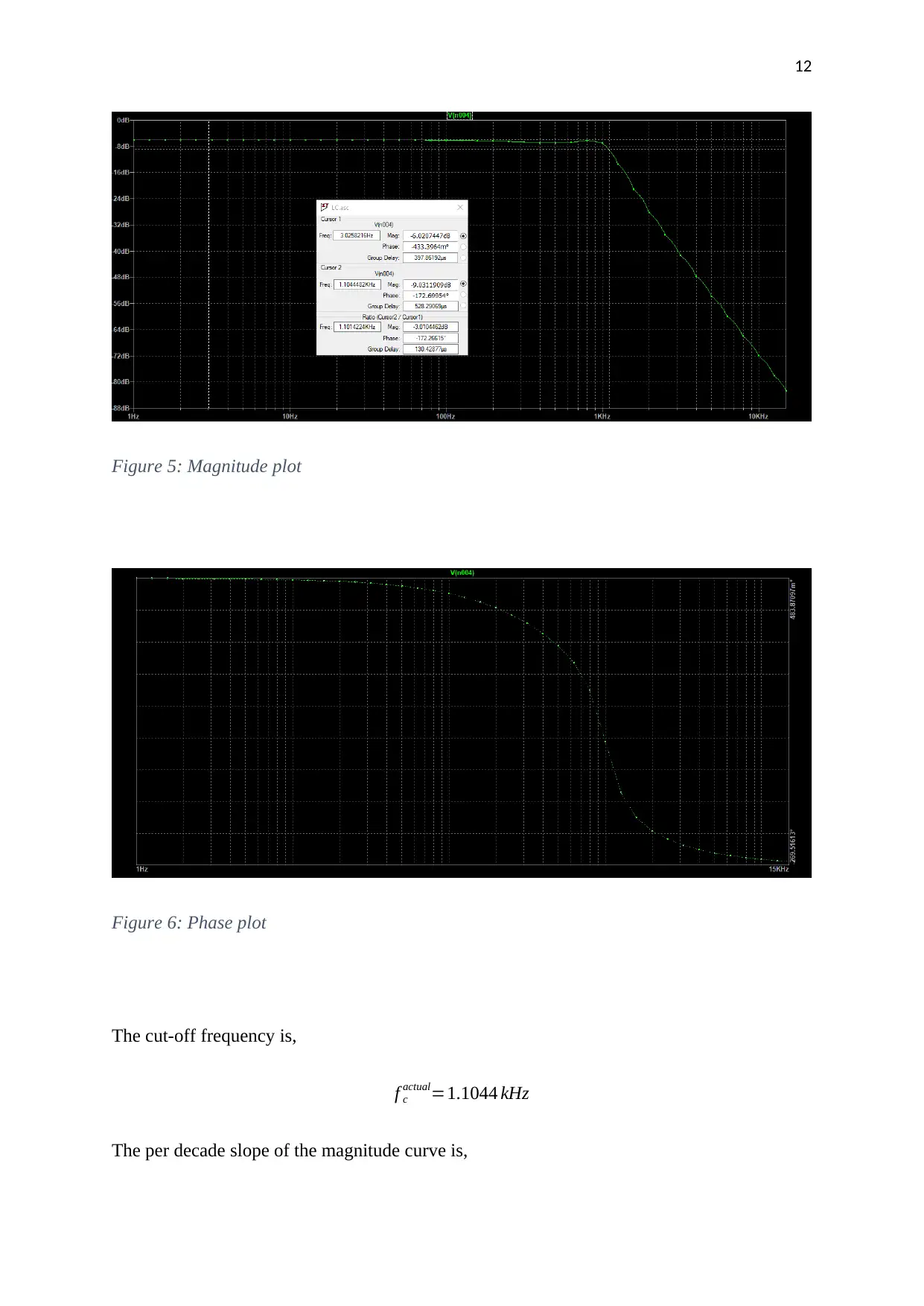
12
Figure 5: Magnitude plot
Figure 6: Phase plot
The cut-off frequency is,
f c
actual=1.1044 kHz
The per decade slope of the magnitude curve is,
Figure 5: Magnitude plot
Figure 6: Phase plot
The cut-off frequency is,
f c
actual=1.1044 kHz
The per decade slope of the magnitude curve is,
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 16
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




