University Engineering Systems Analysis and Modeling - Task 2

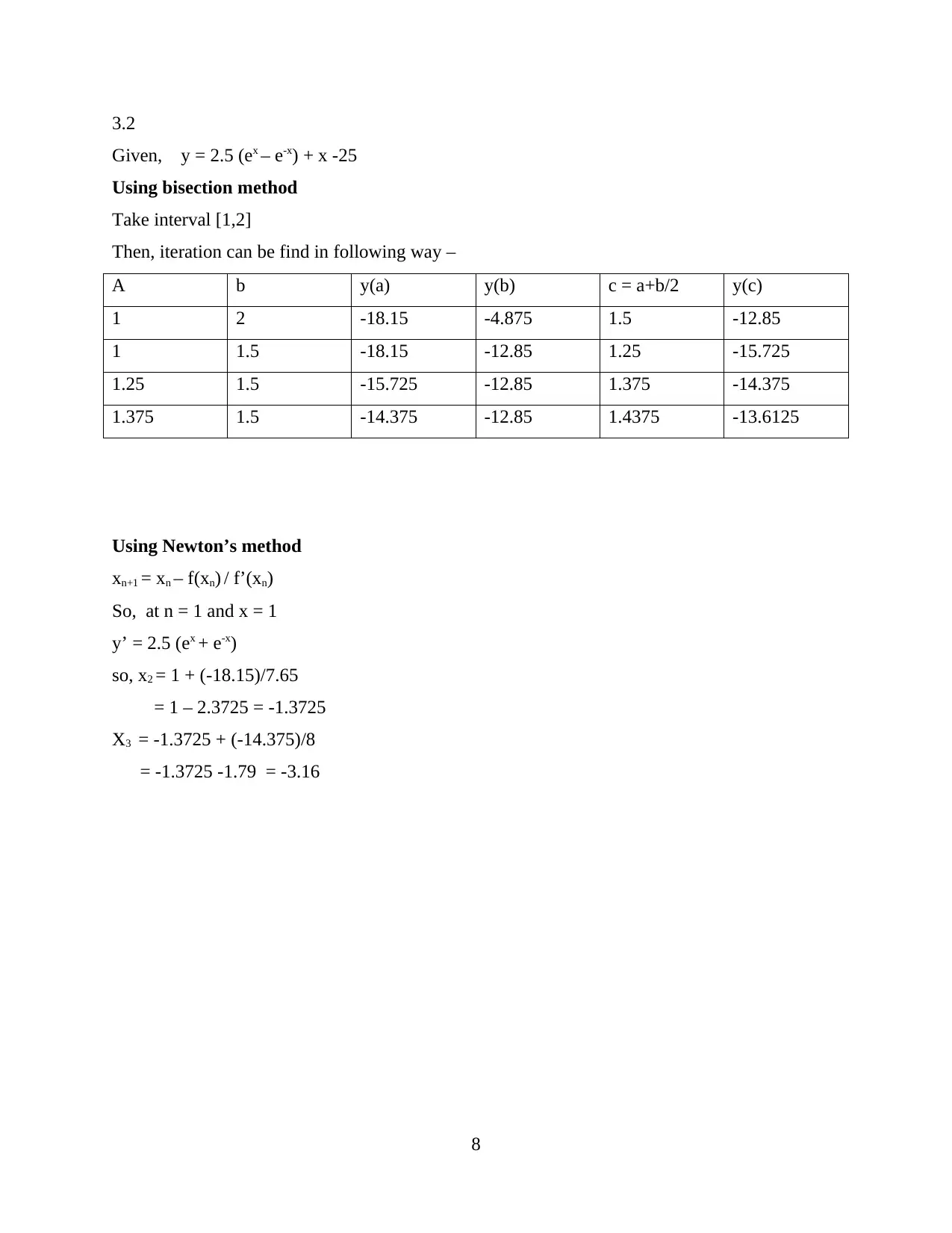
This document provides a comprehensive set of solutions for Task 2 of an engineering systems analysis assignment. It begins by calculating the determinant of a 3x3 matrix and then delves into solving three closed loops of a DC circuit using Kirchhoff's laws, employing both substitution and Gaussian elimination methods. The solution further explores matrix solutions using inverse matrices. The document then moves on to analyze voltage calculations in a circuit with a resistor and capacitor over time and calculates the atmospheric pressure at various altitudes using exponential equations. Furthermore, the document utilizes the bisection and Newton's methods to find the root of a non-linear equation. The assignment also includes the integration of a current function using the trapezoidal rule and the creation of a mathematical model to solve a first-order linear differential equation. Finally, the document provides solutions for differential equations in LCR circuits using Laplace Transforms and other methods.

Analyse and Model Engineering
System

TASK 2.0
2.1 To find the determinant of 3x3 matrix -
1 2 3
0 -4 1
0 3 -1
Solution: Determinant of 3 x 3 matrix can be calculated by using formula -
A = a b c
d e f
g h i
then, determinant of A can be determined by using -
A = a (ei – fh) – b (di – fg) + c (dh - eg)
Let determinant of given matrix is given by A
i.e.
A = 1 2 3
0 -4 1
0 3 -1
then, determinant of A = [ 1 ( -4 x -1 – 1 x3) - 2 ( 0 x -1 – 1 x 0 ) + 3 (0 x 3 – 1 x 0) ]
= [ 1 (4 – 3) – 2 ( 0 – 0) + 3 ( 0 – 0 )]
= 1
1

2.2 Three closed loops of a D.C. Circuit is given by -
2 x + 3 y – 4 z = 26
x – 5 y – 3 z = -87
-7 x + 2 y + 6 z = 12
To determine current flow, by Kirchoff's laws
Solutions: Kirchoff's Laws – this law states that at any node or junction in an electrical circuit,
algebraic sum of entire flow of current meet at zero in a network of conductors. Therefore, using
this law, current flow in given closed loops of DC, can be determined by Using Loop Current
Analysis to find unknown variables -
2 x + 3 y – 4 z = 26 ...(i)
x – 5 y – 3 z = -87 ...(ii)
-7 x + 2 y + 6 z = 12 ...(iii)
Using substitution method,
From equation (i),
x = 26 – 3 y + 4 z ...(iv)
2
Put this value of x into equation (ii),
26 – 3 y + 4 z - 5 y – 3 z = -87
2
26 – 3 y + 4 z – 10 y – 6 z = -174
- 13 y – 2 z = -200
13 y = 200 – 2z
y = 200 – 2z
13
Put this value of y in equation (iv) then,
x = 26 – 3 (200 – 2z ) + 4 z
13
2
x = 338 – 600 – 3 z + 52 z
26
2

x = 49 z – 262
26
Now, put value of x and y in equation (iii)
then,
-7 (49 z – 262) + 2 (200 - 2z) + 6 z = 12
26 13
- 343 z + 1834 + 800 – 8z + 156 z = 312
-195 z = -2322
z = 11.90
so, x = 49 (11.90) – 262 = 12.35 and
26
y = 200 – 2z = 200 – 2 x 11.90 = 13.55
13 13
So, x = 12.35, y = 13.55 and z = 11.90
2.22 Find value of x, y, z by using Guassian elimination method
Linear vector equation, in matrix form -
2 3 -4 x = 26
A = 1 -5 3 y = -87
-7 2 6 z = 12
Now, using Guassian Elimination method,
2 3 -4 26
1 -5 -3 -87
-7 2 6 12
Use R1 → ½ R1
1 3/2 -2 13
1 -5 -3 -87
-7 2 6 12
3

Use R2 → R2 - R1
1 3/2 -2 13
0 -13/2 -1 -100
-7 2 6 12
Use R3 → R3 + 7 R1
1 3/2 -2 13
0 -13/2 -1 -100
0 25/2 -8 103
So, solving this,
we get, x = 10
y = 14
z = 9
2.23 Matrix solution using inverse matrix
Let A X = B
2 3 -4 x 26
A = 1 -5 3 X = y B = -87
-7 2 6 z 12
Using inverse matrix -
so, X = B A-1
Now, A-1 = 1 AT
det.A
So, A-1 = 1 -36 27 -33
-21 -26 -16 -25
-11 -10 -13
A-1 = 1 -36 27 -33
-21 -26 -16 -25
-11 -10 -13
4

So,
x 1 -36 27 -33 26
y = -21 -26 -16 -25 -87
z -11 -10 -13 12
x = 10
y = 14
z = 9
5

3.1
a) Equation of voltage is given by -
vc = 120(1 – e -t/CR ),
Here, R = 47kΩ and C = 15 uF
at t = 0 sec,
vc = 120(1 – e0 )
vc = 0 V
Now, t = 1 sec,
vc = 120(1 – e -1/15x47 )
vc = 120 (1 – e-1/705 )
= 120 (1 – 0.9985)
= 120 x 0.0015 = 0.18V
At time t = 2 sec,
vc = 120(1 – e -2/15x47 )
vc = 120 (1 – e-2/705 )
= 120 (1 – 0.9976)
= 120 x 0.0024 = 0.288V
At time t = 3 sec,
vc = 120(1 – e -2/15x47 )
vc = 120 (1 – e-2/705 )
= 120 (1 – 0.9976)
= 120 x 0.0024 = 0.288V
Therefore, at different values of t, voltage can be determined with fixed coulomb charges as
shown in following graph –
Time Value of
voltage
0 sec 0
1 sec 0.18 V
2 sec 0.288 V
6

b) Given atmospheric pressure p, altitude
Altitude (h) Pressure (p)
500 73.9
1500 68.42
3000 61.6
5000 53.56
8000 43.41
Where,
p = a. ekh
then, ekh = p/a
or, kh = log p –log a
or, k = 1/h (log p –log a)
at h = 500, p = 73.9
k = 1/500 (log 73.9 – log a)
= 1/500 (1.86 – log a) ….(i)
Similarly, at h = 1500, p = 68.42
k = 1/1500 (log 68.42 – log a)
= 1/1500 (1.83 – log a) …(ii)
Similarly, on solving both equations,
1/500 (1.86 – log a) = 1/1500 (1.83 – log a)
1.86 – log a = 1/3 (1.83 – log a)
Log a = 1.375
Or, a = e1.375 = 3.95
Therefore, k will be = 0.001
7

3.2
Given, y = 2.5 (ex – e-x) + x -25
Using bisection method
Take interval [1,2]
Then, iteration can be find in following way –
A b y(a) y(b) c = a+b/2 y(c)
1 2 -18.15 -4.875 1.5 -12.85
1 1.5 -18.15 -12.85 1.25 -15.725
1.25 1.5 -15.725 -12.85 1.375 -14.375
1.375 1.5 -14.375 -12.85 1.4375 -13.6125
Using Newton’s method
xn+1 = xn – f(xn) / f’(xn)
So, at n = 1 and x = 1
y’ = 2.5 (ex + e-x)
so, x2 = 1 + (-18.15)/7.65
= 1 – 2.3725 = -1.3725
X3 = -1.3725 + (-14.375)/8
= -1.3725 -1.79 = -3.16
8

3.3
30 x 10-3
Given, q = ∫ i.dt
0
Using, trapezoidal rule,
Time (ms) Current A
0 0
5 4.8
10 9.1
15 12.7
20 8.8
25 3.5
30 0
9

3.4
Mathematical model -
dp = 3(1+t) – p
dt
it can be written as -
p + dp/dt = 3(1+t)
which is in the form first order linear differential equation, as dy/dx + Py = Q
so, it can solve as -
P (I.F) = ∫ Q x I.F dt
here, Integrating Factor (I.F.) = e∫P.dt
in context with given equation, here, P =1, Q = 3(1+t) and I.F. = e∫1.dt = et
so, p. et = ∫ 3(1+t) et .dt
p . et = 3[ ∫et. dt + ∫t.et .dt ]
p . et = 3.et + 3 [ t. ∫ et - ∫ d(t)/dt ∫ et .dt ]
p . et = 3 et + 3 (t -1) et
p . et = 3 et + 3t – 3 et
p = 3 t + e1-t
10