Detailed Report on Modulus of Elasticity of Reinforced Concrete

This report provides a detailed analysis of the modulus of elasticity of reinforced concrete, explaining the concepts behind finding the modulus of elasticity for both concrete and steel, based on Hooke's Law. It differentiates between short-term and long-term elastic strains, detailing methods to calculate the short-term modulus of elasticity (Ec) using Initial Tangent Modulus, Tangent Modulus, and Secant Modulus methods, along with the empirical formula from IS 456-2000. Furthermore, it explains how to determine the Effective modulus of Rigidity (Ece) using the creep coefficient. The report includes a solved problem for grade 30 concrete, demonstrating the calculation of both short-term and long-term Young’s modulus. Finally, it provides the formula to find the Equivalent Young’s modulus of reinforced concrete, including a detailed example with calculations for a doubly reinforced concrete section, and also provides a method for problems involving circular cross sections. The document concludes with references to relevant research papers and books.

Modulus of elasticity of Reinforced
Concrete

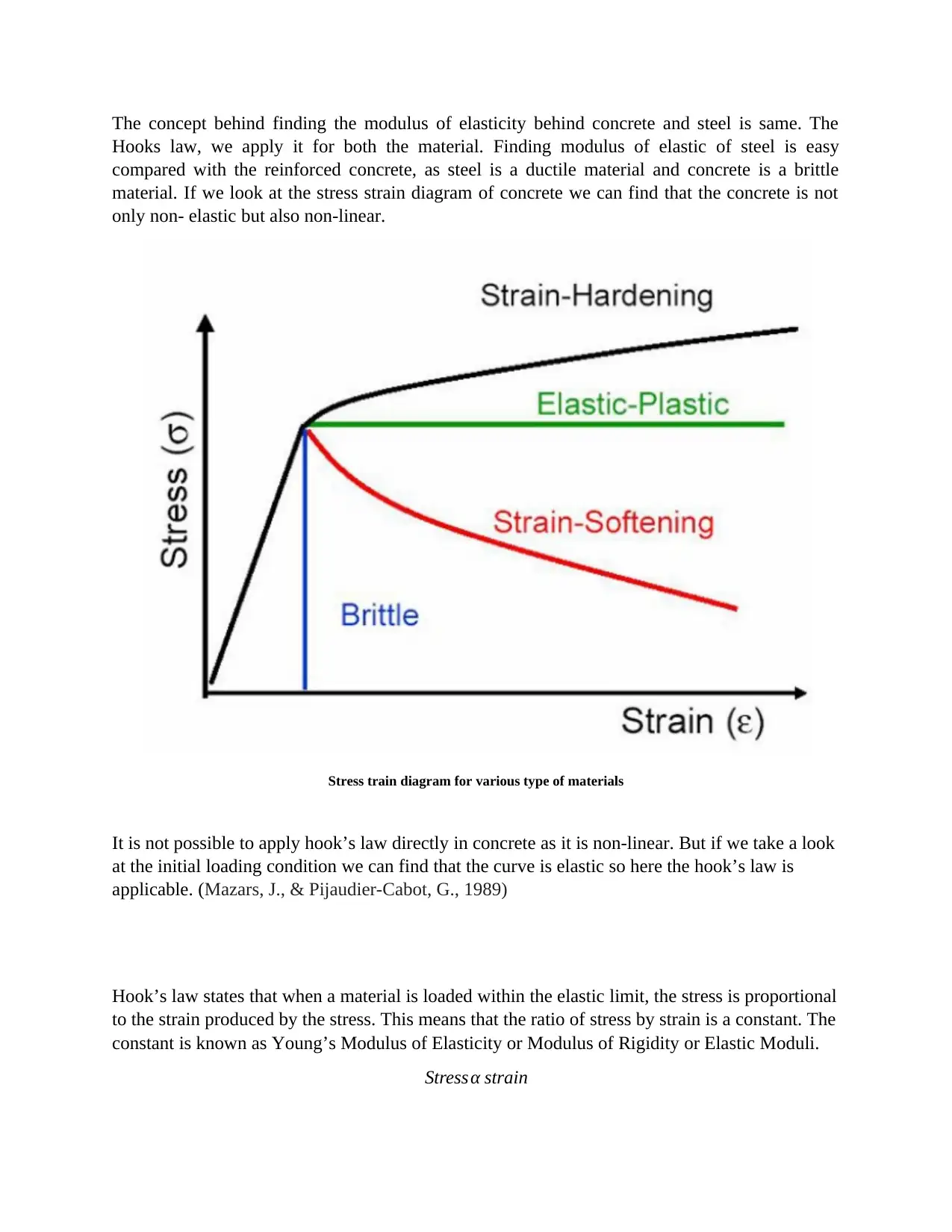
The concept behind finding the modulus of elasticity behind concrete and steel is same. The
Hooks law, we apply it for both the material. Finding modulus of elastic of steel is easy
compared with the reinforced concrete, as steel is a ductile material and concrete is a brittle
material. If we look at the stress strain diagram of concrete we can find that the concrete is not
only non- elastic but also non-linear.
Stress train diagram for various type of materials
It is not possible to apply hook’s law directly in concrete as it is non-linear. But if we take a look
at the initial loading condition we can find that the curve is elastic so here the hook’s law is
applicable. (Mazars, J., & Pijaudier-Cabot, G., 1989)
Hook’s law states that when a material is loaded within the elastic limit, the stress is proportional
to the strain produced by the stress. This means that the ratio of stress by strain is a constant. The
constant is known as Young’s Modulus of Elasticity or Modulus of Rigidity or Elastic Moduli.
Stress α strain

stress
strain = E
E= σ
e N/mm2
In case of concrete there are two types of strain the short term elastic strain and the long term
elastic strain. The short term elastic strain are due to instantaneous load applied on concretre and
long term strain are due to effect of creep and shrinkage. Because of this situation modulus of
elasticity due to short term elastic strain is called short term modulus of elasticity Ec. Long term
strain it is called Effective modulus of elasticity denoted by Ece. (Triantafillou, T. C., &Plevris,
N., 1992)
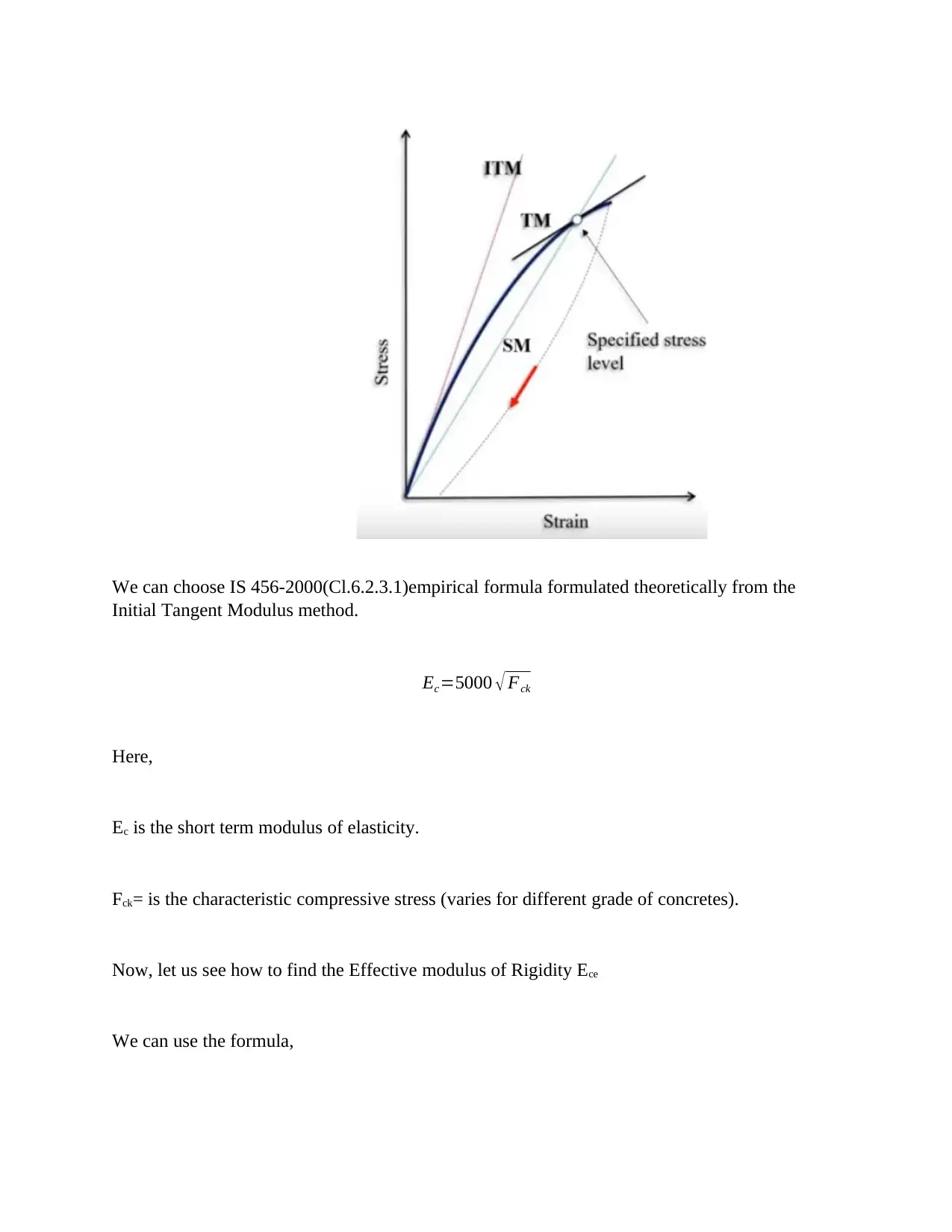
Now, let us see how to find the short term modulus of elasticity Ec
There are three methods to find the short-term modulus Ec
They are
1. By draw a tangent line for the obtained stress and strain curve from the origin
known as Initial Tangent Modulus (ITM) method.
2. By choosing a specific stress level and drawing a tangent at this point, known as
Tangent Modulus (TM) method.
3. By connecting the stress level to origin and obtaining a value known as secant
modulus (SM) method.

We can choose IS 456-2000(Cl.6.2.3.1)empirical formula formulated theoretically from the
Initial Tangent Modulus method.
Ec=5000 √ Fck
Here,
Ec is the short term modulus of elasticity.
Fck= is the characteristic compressive stress (varies for different grade of concretes).
Now, let us see how to find the Effective modulus of Rigidity Ece
We can use the formula,

Ece= Ec
1+ θ
Here,
Ece= Effective modulus of Rigidity
Ec= short term modulus of elasticity.
θ = Creep coefficient
The creep coefficient will be provided in a standard Design Data book (IS 456-2000 (CI. 6.
2.5.1)). The creep coefficient changes according to the days of which the concrete is casted.
Now, let us solve a problem for a reinforced concrete of grade 30. Which is casted before 28
days.
Wkt,
Ec=5000 √ Fck
Fck = 30Mpa for grade 30
Ec=27390 MP a
The short term Modulus of elasticity is found to be 27390 MPa
Now find the long term Young’s modulus
Ece= Ec
1+ θ
For creep coefficient from data book for 28 days we can take 1.6

Now,
Ece =10530 MP a
The Effective modulus of elasticity Ece is found to be 10530 MPa
In order to find the Equivalent young’s modulus of the reinforced concrete we have the
formula as,(Chen, W. F., 2007)
EI =Ec I c + Es Is
Where,
E = Equivalent Young’s modulus
Es = Young’s modulus of steel
Ec= Young’s modulus of concrete
I = Total cross sectional moment of inertia
Ic = Cross sectional moment of inertia of concrete
Is = Cross sectional moment of inertia of steel
A cross section of a doubly reinforced concrete will look as,

In this we can see the concrete is reinforced with 4 number of steels, we need to calculate the
area moment of inertia of steel and concrete.
Cross sectional moment of inertia of steel (cicular) , Is= Π
64 d4
mm4
Cross sectional moment of inertia of concrete (rectangle- n circles),Ic-x = b h3
12 −n ( Π
64 d4
)mm4
Where,
n = number of steel rods inside the concrete.
Total cross sectional moment of inertia, I = b h3
12 mm4
By substituting these known values in the equation we can get, Equivalent young’s modulus, E
E= Ec Ic+ Es I s
I
Example:
Find the equivalent young’s modulus of a grade 30 concrete reinforced with steel of C 35 grade?
Take b = 0.25 m, h = 0.5 m, steel rod diameter, d = 0.025 m
Solution:
We know that young’s modulus of steel C 35,Es = 200000 Mpa
We know that Young’s modulus of concrete grade 30 within elastic limit, Ec = 27390 Mpa
We need to find, E

We have, equivalent young’s moduls of reinforced concrete,
E= Ec Ic+ Es I s
I
Now,
Ic, Is, and I are,
Wkt,
Cross sectional moment of inertia of steel (cicular) , Is= Π
64 d4m4
Is = 1.91650 x 10-8
Cross sectional moment of inertia of concrete (rectangle- 4 circles),
Ic-x = b h3
12 −4 ( Π
64 d4
)m4
Ic-x = 2.6041 x 10-3m4
Total cross sectional moment of inertia,

I = b h3
12 m4
I = 2.60416 x 10-3
Now substitute the values in the equation we get,
E = 27389.789 MPa
Thus the equivalent young’s modulus of the reinforced concrete is found as 27389.789 MPa
For the problems involving circular cross section can be solved similarly, except that the cross
section moment of inertia of concrete formula will vary as the cross section is circular as,
Cross sectional moment of inertia of concrete (rectangle- n circles),Ic-x = ( Π
64 d4
)−n ( Π
64 d 4
)m4
Where,
n = number of steel rods inside the concrete.

References
Mazars, J., & Pijaudier-Cabot, G. (1989). Continuum damage theory—application to
concrete. Journal of Engineering Mechanics, 115(2), 345-365.
Triantafillou, T. C., &Plevris, N. (1992). Strengthening of RC beams with epoxy-bonded fibre-
composite materials. Materials and Structures, 25(4), 201-211.
Chen, W. F. (2007). Plasticity in reinforced concrete. J. Ross Publishing.