Financial Mathematics: Annuity Calculations and Problem Solving
VerifiedAdded on 2022/01/25
|20
|1189
|130
Homework Assignment
AI Summary
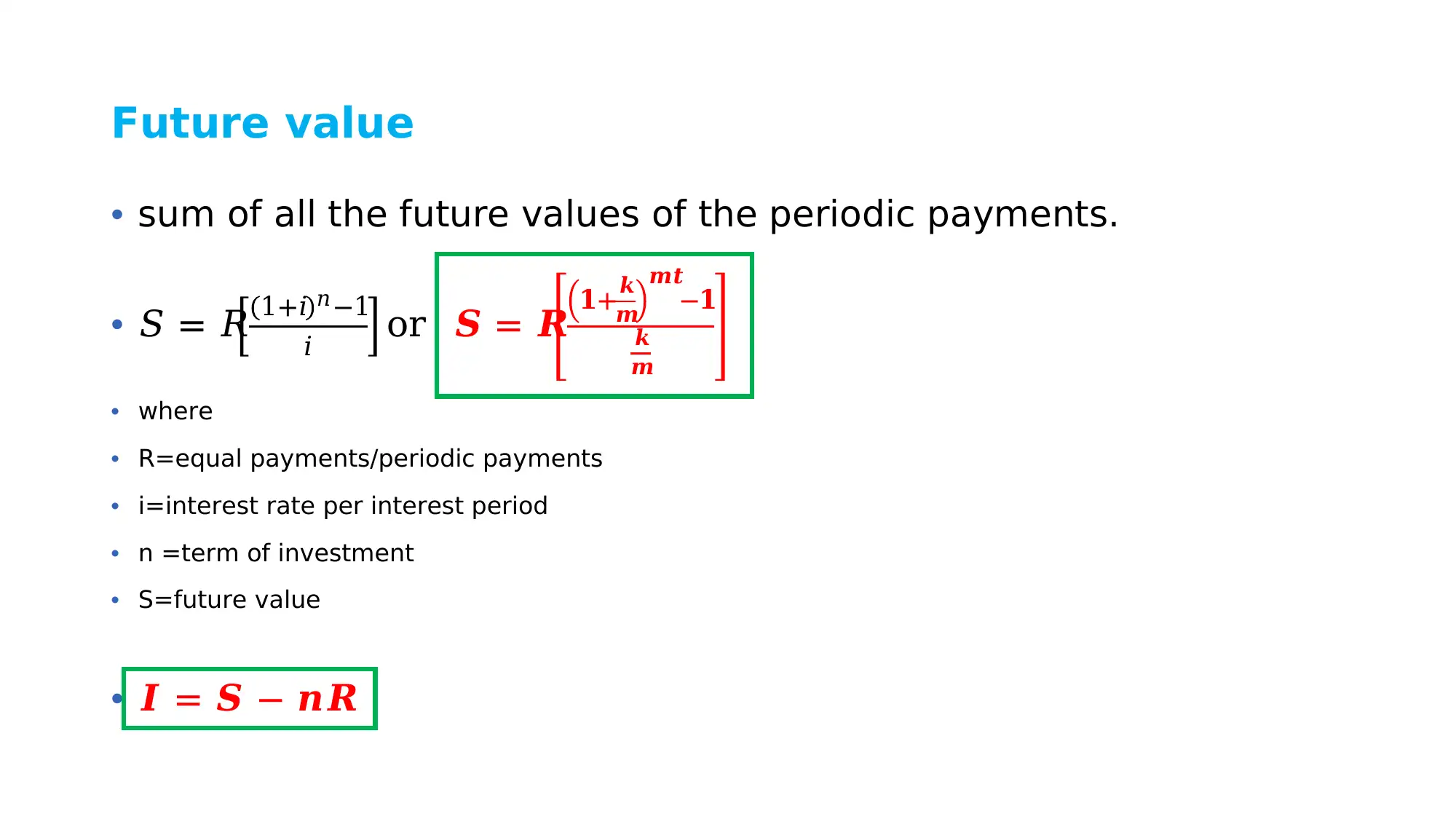
This document provides a detailed explanation of annuities, covering both future and present value calculations. It begins with an introduction to annuities, defining them as a series of equal payments made at equal intervals, and highlights their relevance in financial planning, investment, and loan estimations. The document then delves into the future value of ordinary annuities, providing formulas and worked examples to illustrate how to calculate the future value of periodic payments, including scenarios involving forborne annuities. Following this, the present value of ordinary annuities is explored, with formulas and examples demonstrating how to determine the present value of future payments, including deferred annuity situations. The assignment includes several examples where students are required to calculate annuity payments and interest rates. Additionally, the document showcases how to calculate different variables associated with annuities, such as the number of payments. Overall, the assignment offers a practical guide to understanding and solving a range of annuity problems.
1 out of 20






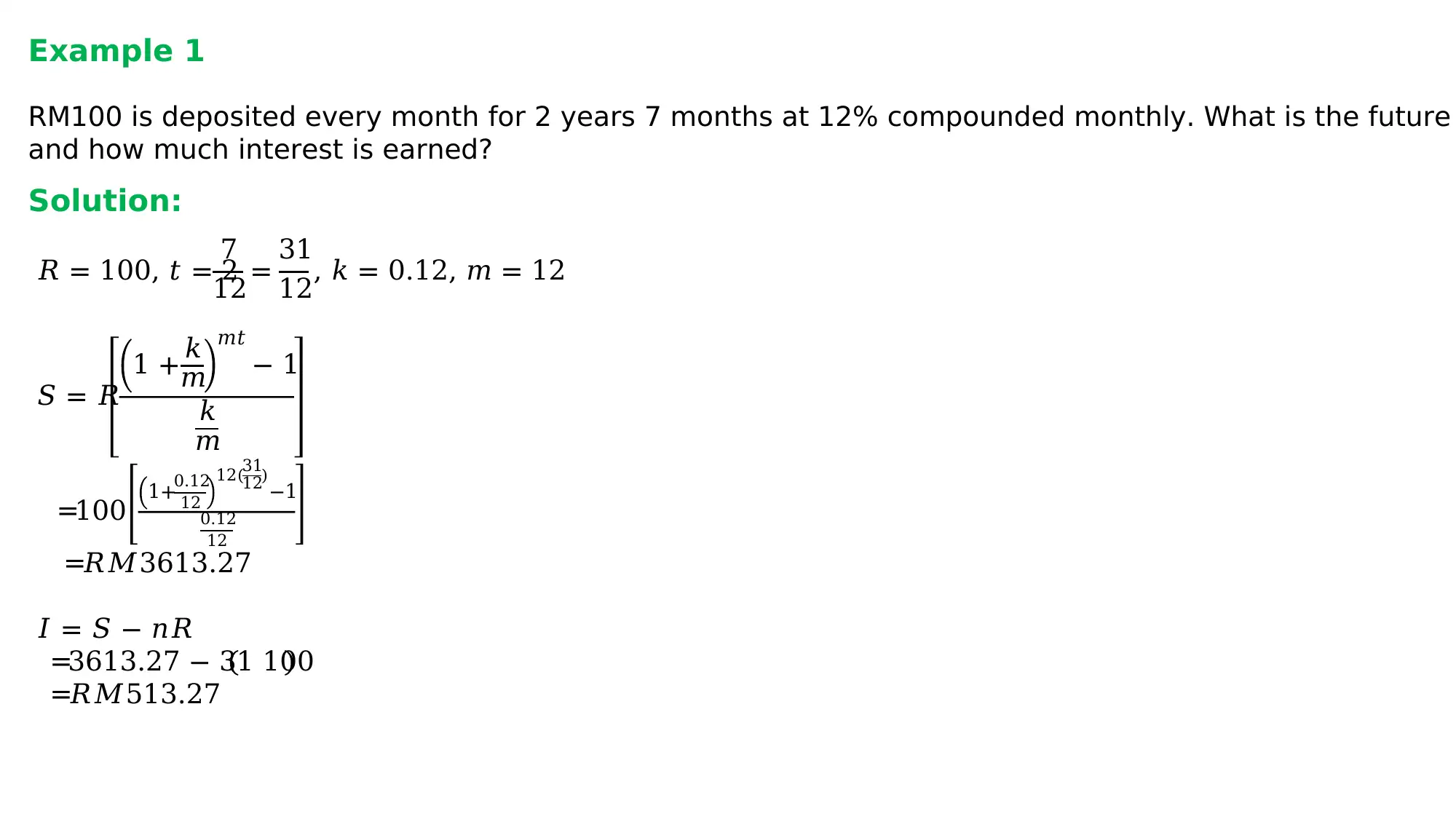











![[object Object]](/_next/static/media/star-bottom.7253800d.svg)