University Calculus Assignment: Applications of Differentiation

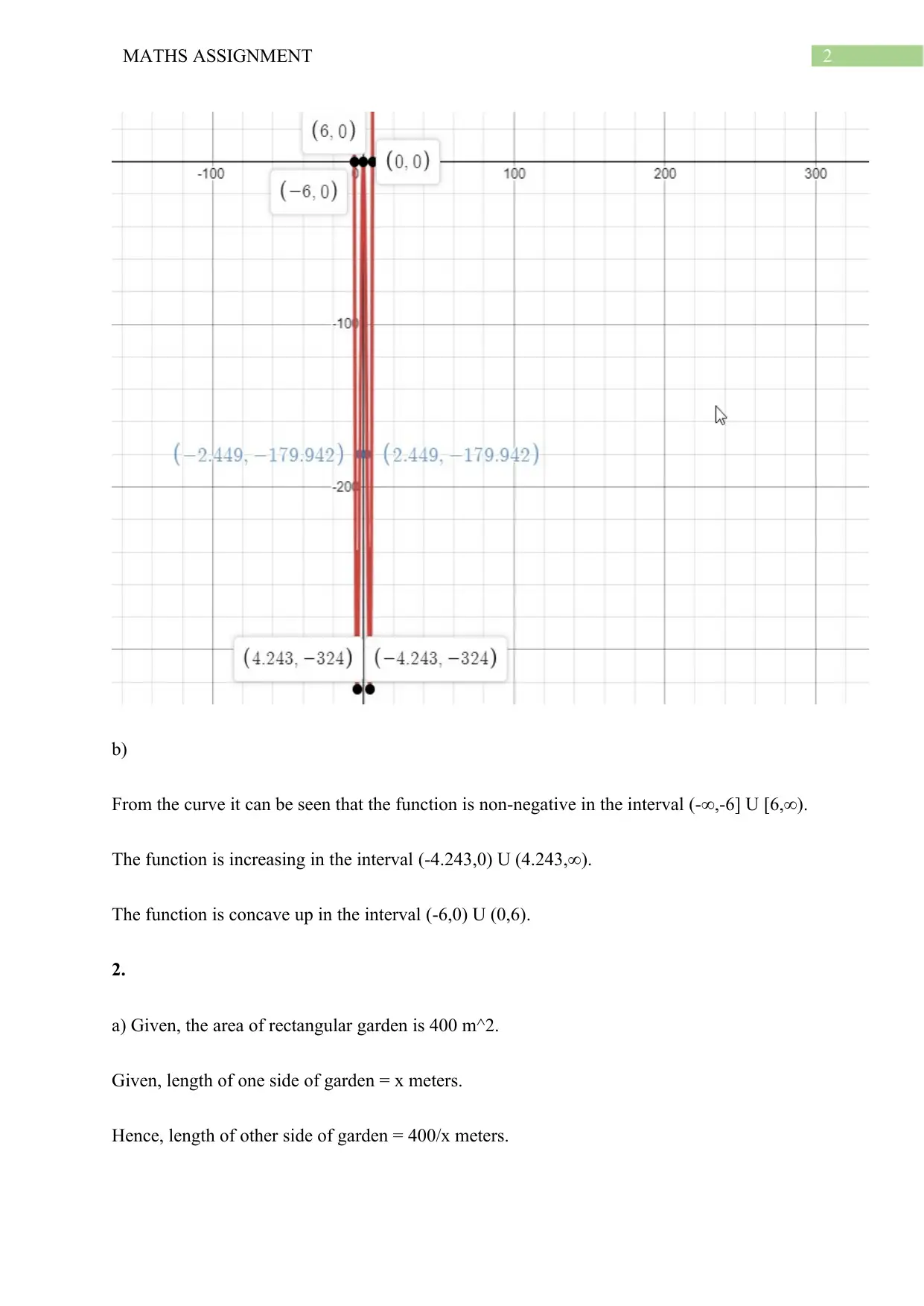
This document presents a comprehensive solution to a maths assignment focusing on the applications of differentiation. The assignment includes three main problems. The first problem involves sketching the graph of a quartic function, identifying x-intercepts, stationary points, and points of inflection, and determining intervals where the function is non-negative, increasing, and concave up. The second problem deals with an optimization scenario where a farmer builds a rectangular garden, requiring the student to model the length of new fencing, find stationary points, and determine the minimum amount of fencing needed. The third problem explores the design of a half-liter container, requiring the student to derive the height of the container, calculate the total surface area, and determine the radius that minimizes the surface area.

Running head: MATHS ASSIGNMENT
MATHS ASSIGNMENT
Name of the Student
Name of the University
Author Note

1MATHS ASSIGNMENT
1.
a) y = x^4 – 36x^2
x-intercept => 0 = x^4 – 36x^2
 x = 0, 6,-6
hence, x intercepts are (0,0), (6,0), (-6,0)
y intercept => y = 0
 (0,0)
Stationary points => dy/dx = 0
 4x^3 – 72x = 0
 (x^2 – 18)x = 0
 x = 0 and x = ± √18 = ±4.242
Hence, points are (0,0), (-4.242,-324), (4.242,324)
Points of inflection => ( d
dx )( dy
dx )=0
 12x^2 – 72 = 0
 x^2 – 6 = 0
 x = ± √ 6 = ±2.449
Hence, points are (-2.449,-179.942) , (2.449,-179.942)
Graph of curve with all points:

2MATHS ASSIGNMENT
b)
From the curve it can be seen that the function is non-negative in the interval (-∞,-6] U [6,∞).
The function is increasing in the interval (-4.243,0) U (4.243,∞).
The function is concave up in the interval (-6,0) U (0,6).
2.
a) Given, the area of rectangular garden is 400 m^2.
Given, length of one side of garden = x meters.
Hence, length of other side of garden = 400/x meters.

3MATHS ASSIGNMENT
Now, new fencing will be made by remaining sides of garden without the existing fencing of
two sides.
Hence, the length of fencing is the combined length of two sides = x + 400/x meters when x
>0.
b) dL/dx = 1 – 400/x^2
Stationary points => dL/dx = 0
 1 – 400/x^2 = 0
 x^2 = 400
 x = 20 meters as x>0
Hence, the stationary point of L is (20,40)
c) Now, ( d
dx )( dL
dx ) = 2*400/x^3 = 800/x^3
Now, only one feasible stationary point is (20,40).
Now, the stationary point is minimum if ( d
dx )( dL
dx )(20,40)
> 0
( d
dx )( dL
dx )(20,40)
= 800
203 > 0
Hence, the point (20,40) is minimum.
Thus the new value of x = 20 meters for which L is minimum and minimum amount of new
fencing required is 40 meters.

4MATHS ASSIGNMENT
3.
Given, radius of ½ litre container = r cm.
Given, height of ½ litre container = h cm.
Hence, volume = π r2 h cm^3 = π r2 h
1000 litre
Hence, π r2 h
1000 = 1
2
 h = 500
π r2 when r > 0
b) Total surface area of a container that is open at the top is given by,
A = π r2+ 2 πr∗h = π r2+ 2 πr∗500
π r2 = π r2+ 1000
r
c) A is minimum for the r for which
dA/dr = 0 and ( d
dr )( dA
dr )>0
 2 π r −1000
r2 = 0
 r3 =1000
2 π
 r =5.419 cm
Now, ( d
dr )( dA
dr )r =5.419
=
(2 π +2000
r3 )r=5.419
= (2 π + 2000
5.4193 )>0
Hence, at r = 5.419 cm the surface area is minimum.

5MATHS ASSIGNMENT
The minimum value of surface area A = π∗5.4192+ 1000
5.419 = 276.79 cm^2.
.