Applied Mathematics for Engineers: Wave Analysis and Systems

This assignment solution covers several key areas of applied mathematics relevant to engineering. It begins with an analysis of wave properties, including frequency, period, and amplitude calculations for sinusoidal functions. It then delves into the analysis of a mass spring damper system, solving for displacement, velocity, and acceleration using both Gaussian elimination and Cramer's method. The assignment continues by solving a system of equations, including quadratic equations, and trigonometric equations. Finally, the assignment addresses an optimization problem, calculating the largest area of a rectangular field given a fixed perimeter, demonstrating the application of mathematical concepts to real-world engineering scenarios.

Applied Mathematics For
Engineers

TABLE OF CONTENTS
PART 1............................................................................................................................................1
Task 1.....................................................................................................................................1
Task 2.....................................................................................................................................4
PART 2............................................................................................................................................8
Task 3.....................................................................................................................................8
Task 4...................................................................................................................................11

PART 1
Task 1
1) find the frequency, periodic time, amplitude of two waves
a) F(t) = 10 cos (4/3 t)
the amplitude is the maximum value of the function,
the amplitude can be defined as the maximum distance the wave can travel from its centre.
Here the maximum value is 10, so the amplitude = 10
to find out the period, it can be found out as
period = 360 / (4/3)
period = 270 degree
Frequency can be measured as the number of wave complete in each 180 degree.
The frequency can be given as f = c/ λ
where,
c = speed of sound, which is 343 m/s.
f = frequency
λ = wave length
here, ω = 4/3
so, f = 1/T
or it can also be written as;
f = ω/2π
f = (4/3)/2*3.14
f = 0.21 Hz
now, the time period can be given as; f = 1/T
so, T can be expressed as T = 1/f
T = 1/0.21
T = 4.76 seconds.
b) F(t) = 10 sin (3t)
here, the maximum value is 10, so it is very mush easy to find out the amplitude,
amplitude of this wave = 10.
the ω can be give here, which is given as 3.
1

with the help of ω, we can find out the frequency. The formula of frequency given is;
f = ω / 2π
f = 3/2*3.14
f = 0.477 Hz
after finding out the frequency, the time period can be found out here, which is
T = 1/f
T = 1/0.477
T = 2.093 seconds.
c) the displacement can be modified by any sinusoidal functions, which is given as;
= 2 cos x + √3 Sin x
the new form, which will be converted into R sin (x+a), where R>0 and 0<a<90 degree.
The value of R and x have to be found out here,
we have to convert this equation, which can be done as;
we will only take the positive sign, so that it will be easy for us to calculate;
therefore;
2 cos x + √3 Sin x = R sin (x+a)
the formula can be applied here to open the brackets,
sin(a+b) = sin A cos B + cos A sin B
in the same way, we can expand this equation as;
R sin (x+a) = R (sin x cos a + cos x sin a)
= R sin x cos a + R cos x sin a
So, by the above equations we can say that;
√3 Sin x + 2 cos x = R cos a sin x + R sin a cos x
now, equating all the co efficient of sin and cos in the above equation, we are having;
for sin x : √3 = R cos a … (i)
for cos x : 2 = R sin a … (ii)
divide equation (ii)/(i)
2/√3 = R sin a/ R cos a
2/√3 = tan a
a = arc tan (2/√3)
a = 0.857 degree
2

here the angle a is a positive acute angle.
Now, we have to find out the value of R, so we need to square both the equations and add them,
(√3)^2 + (2)^2 = R^2 cos ^2 a + R^2 sin ^2 a
3 + 4 = R^2( cos^2 a + sin^2 a)
7 = R^2
therefore; R = 2.645
We also have to find out the values of x, which can be given by the following equation;
2 cos x + √3 Sin x = 1
√3 Sin x = 1 – 2 cos x
to remove the square root, we will make square of both the sides, hence, they are
3 sin^2 x = 1 – 4 cos x + cos ^2 x
by the help of Pythagorean theorem;
3 (1- cos^2 x) = 1-4 cos x + cos^2 x
3 – 3 cos^2 x = 1 – 4 cos x + cos^2 x
2 + 4 cos x - 4 cos^2 x = 0
2( 1 + 2 cos x – 2 cos^2 x) = 0
- 2 cos^2 x + 2 cos x + 1 = 0
( -2 cos x+1) (cos x +1) = 0
from this equation, one angle is becoming negative, so we can not take that. The other one is
positive, which is;
cos x = ½
x = arc cos ½
x = 1.047 degrees
d) solutions of the equations given below;
i) cos^2 (x)- sin^2 (x) = 1
this can also be written as; L.H.S
= 2 cos^x – 1
= 1 – 2 sin^2 x
= 1- (½ – ½ cos (2x))
the rest of the terms can be given as 0.
Because ½ of cos (2x) can not be put up in the table, so it can be termed as 0
3

therefore, L.H.S = 1-0 = 1
L.H.S = R.H.S, proved
ii) 10 sin (x+10) = 2.5
sin(a+b) = sin A cos B + cos A sin B
= 10 (sin x cos 10 + cos x sin 10)
= 10 ( sin x * (-0.83) + cos x (-0.544)
= 10 ( -0.83 sin x – 0.54 cos x)
by squaring of both the sides
6.25 = 100 ( 0.83^2 sin ^2 x – 0.54^2 cos^2 x)
6.25 = 100 [ 0.063( sin^2 x + cos^2 x)
therefore,
6.25 = 6.3 *1
L.H.S = R.H.S
Task 2
2) mass spring damper system, acceleration given here is X3, and the velocity given is
X2, and displacement is X1. The question here given is
12.6 7.9 6.2 x1 = 18.0
4.8 4.8 7.5 x2 = 6.39
-13 3.5 13 x3 = -17.40
we will multiply all the factors inside the given values, and hence form the three equations,
which is;
12.6 x1 + 7.9 x2 + 6.2 x3 = 18
4.8 x1 + 4.8 x2 + 7.5 x3 = 6.39
-13 x1 + 3.5 x2 + 13 x3 = -17.4
the equation can be written in the form of matrix as;
12.6 7.9 6.2 = 18
4.8 4.8 7.5 = 6.39
-13 3.5 13 = -17.4
now we have to find out the values of x1, x2 and x3. For that we have to make the diagonal
values 1 and the rest values 0 i.e. identity matrix.
First divide the row 1 by 12.6,
4

1 79/126 31/63 10/7
4.8 4.8 7.5 6.39
-13 3.5 13 -17.4
now, do multiplication of largest area of any rectangular field, which can be enclosed by a fence,
which is having a length of 800 m row 1 by 4.8 and subtract it from row 2, and also multiply
row 1 by 13 and add this value in row 3,
i.e. R2 – 4.8 R1 – R2 and R3 + 13 R1 – R3
the matrix will become;
1 79/126 31/63 10/7
0 1 1079/367 -981/3760
0 734/63 1222/63 41/35
now multiply row 2 by 79/126 and subtract it from row 1, at the same time multiply row 2 by
734/63 and subtract it from row 3. After doing this divide row 3 by -2639/188
after following these two steps, the matrix will look like;
1 0 -983/752 11973/7520
0 1 1079/376 -981/3760
0 0 -2639/188 7917/1880
and the final matrix will look like;
1 0 -983/752 11973/7520
0 1 1079/376 -981/3760
0 0 1 -0.3
The column 2 and column 3 have to be zero, so this can be done by multiplying the row 3 by
983/752 and add this is row 1. Similarly multiply row 2 by -1079/376 and subtract this from row
2, the final matrix will become;
1 0 0 1.2
0 1 0 0.6
0 0 1 -0.3
so the values of x1 = 1.2 x2 = 0.6 and x3 = -0.3
we have to compare this with Cramer's method, so we will use the triangle's rule to calculate the
determinant of matrix.
5

∆ = 12.6 7.9 6.2
4.8 4.8 7.5
-13 3.5 13
by using the triangle rule;
= 12.6*4.8*13 + 7.9*7.5*-13 + 6.2*4.8*-13 – 12.6*7.5*3.5 – 7.9*4.8*13
= -7917/25
∆ 1 = 18 7.9 6.2
6.39 4.8 7.5
-17.4 3.5 13
after doing the calculation by triangle, it will comes out as = -47502/125
for the second determinant,
∆ 2 = 12.6 18 6.2
4.8 6.39 7.5
-13 -17.4 13
= 12.6*6.39*13 + 18*7.5*-13 + 6.2*4.8*-17.4 – 6.2*6.39*-13 – 12.6*7.5*-17.4
= -23751/125
and for the final determinant,
∆ 3 = 12.6 7.9 18
4.8 4.8 6.39
-13 3.5 -17.4
by using the same formulas, the values will come out as;
x1 = ∆ 1/∆ = (-47502/125)/(-7917/25)
= 6/5
x2 = ∆ 2/∆ = (-23751/125)/(-7917/25)
= 3/5
x3 = ∆ 3/∆ = (23751/125)/(-7917/25)
= -3/10
hence it is clearly shown that by using Gaussian elimination method and by using Cramer's
method, the values of x1, x2 and x3 remains same, and that is
x 1 = 1.2
x 2 = 0.6
6

x 3 = -0.3
3) the equations are;
X -Y = 2 … (i)
and X^2 +Y^2 = 34 … (ii)
from the equation (I)
Y = X-2
so we put this value in equation (ii)
X^2 + (X-2)^2 = 34
X^2 + (X-2)(X-2)= 34
X^2 + X^2 – 4X + 4 = 34
2 X^2 – 4 X + 4 = 34
2 X^2 – 4 x – 30 = 0
take 2 common;
X^2 – 2 X – 15 = 0
take the factors of this equation, which will come as;
(X-5)(X+3) = 03
two solutions will be there from this, one is X = 5, then Y = -3
and second is if X = -3, then Y = +5
4) x^3 – 3.25 X^2 + x – 0.063 = 0
and Sin 5y – Sin 3y = 0.58
for the value of x, we will take x common from that equation, then it will become;
x( x^2 – 3.25 x 1 + 1) = 0.063
or it can also be found out as;
x = -b +- √ b^2 – 4ac / 2a
= 3.25 + √ 3.25^2 – 4*1*1 / 2*1
x = 3.25 + 2.56173 / 2*1
x = 2.9058,
if we are taking the value of this formula as negative, then
x = 3.25 - √ 3.25^2 – 4*1*1 / 2*1
x = 0.3441
and for the value of y, the equation given here is; Sin 5y – Sin 3y = 0.58
7

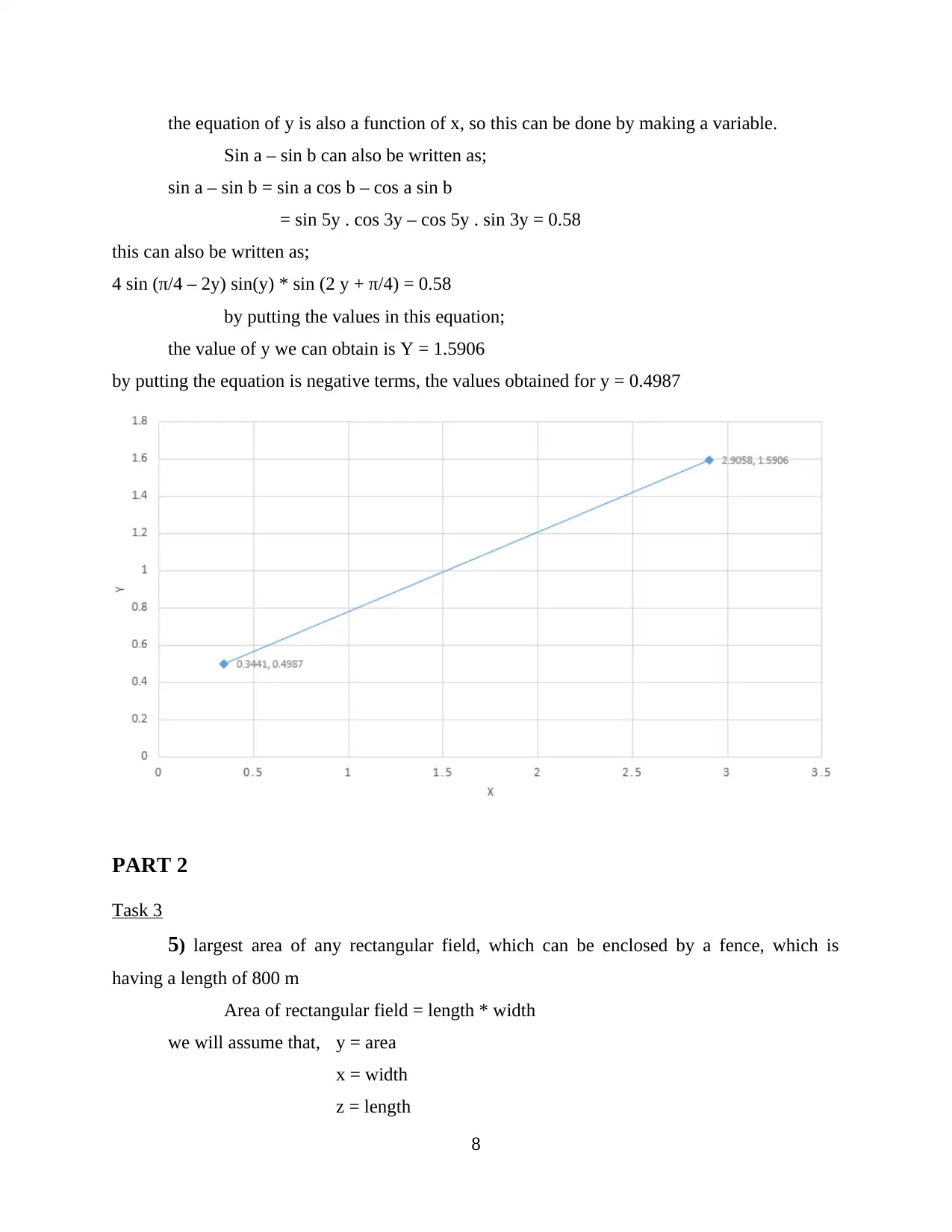
the equation of y is also a function of x, so this can be done by making a variable.
Sin a – sin b can also be written as;
sin a – sin b = sin a cos b – cos a sin b
= sin 5y . cos 3y – cos 5y . sin 3y = 0.58
this can also be written as;
4 sin (π/4 – 2y) sin(y) * sin (2 y + π/4) = 0.58
by putting the values in this equation;
the value of y we can obtain is Y = 1.5906
by putting the equation is negative terms, the values obtained for y = 0.4987
PART 2
Task 3
5) largest area of any rectangular field, which can be enclosed by a fence, which is
having a length of 800 m
Area of rectangular field = length * width
we will assume that, y = area
x = width
z = length
8

therefore; y = x * L . . . (i)
so, the area can be given as; perimeter, whichh can be length, i.e. 800
P = 2*length + 2*width
800 = 2L + 2x
divide the above equation by 2,
400 = L + x
We will solve this equation for finding out the value of L;
400 – x = L … (ii)
put this value of L in equation (i)
y = x *(400 – x)
y = 400 x – x^2
Now if we write this equation in its descending order; that will be
y = -x^2 + 400 x
the co-efficient of x^2 here is negative, so for solving this equation, the vertex formula can be
used, because it looks like a parabola, which will ,move downwards.
The vertex of a parabolic equation can be written as;
y = ax^2 + bx + c
So, for this particular equation, the x coordinate is = -b/2a
the y coordinates can be found out by substituting the values
the equation of y can be written as;
y = -1x^2 + 400 x +0
here, a= -1, b = 400, c = 0
so for the coordinates x = -b / 2a
x = -400/2*-1
x = 200 m
the length of the rectangle can be found out by putting this value of x in equation (ii)
400 – x = L
400 – 200 = L
therefore; L = 200 m
it is clear that the maximum area of the rectangle can only be found, when the length and breadth
of the rectangle is 200 m and 200 m .
9

for calculating the maximum area of this rectangular field, y coordinates have to be known and
that can be found out by;
y = -1x^2 + 400 x +0
y = -1(200)^2 + 400(200) +0
y = -40000 + 80000
y = 40000 sq meters
so, the maximum area of this field would be = 40000 sq meter.
6) rate of change of total surface area of rectangular cone, if the base radius given is = 15
cm, height = 32 cm, if radium is increasing by 15 mm/s, and height by 25 mm/s
The surface area of any rectangular cone = πr^2 + πrl
here; r is the radius
h is the height and
l is the slant height
the volume of the cone can be given as; V = πr^2h/ 3
the surface area can be found out as;
SA = πr^2 + πrl,
the slant height can be found out with the help of Pythagorean theorem, which will be;
slant height = √(32^2 + 15^2)
slant height = 35.34 cm
so the surface area is = 3.14 * 15^2 + 3.14 * 15 * 35.34
= 2371.07 cm ^2
Now if the radius is increasing by 15 mm/s and height by 25 mm/s,
the new radius will be 15+1.5 = 16.5 cm and height = 32 + 2.5 = 34.5
the rate of change of SA = d/dx (πr^2 + πrl)
= π d/dx (r^2 + rl),
= π * 2r r' + rl'
the new slant height will be = √(34.5^2 + 16.5^2
= 38.24 cm
so the new surface area will be = 3.14 * 16.5^2 + 3.14 * 16.5 * 38.24
= 2836.21 cm ^2
so the rate of change of surface area will be = 2836.21 – 2371.07
10

= 465.14 cm
7) volume of concrete required if rotated around x axis initially, and afterwards y aixs
y = x^2 for 0≤x≤1
the volume can be found out by; ∫ 2 πx f(x). dx
f(x)= x^2
so V = ∫ 2 π x. x^2 . dx (the limits here is from 0 to 1)
V = 2 π ∫ (x^3) . dx
V = 2 *3.14 * 3 * 1
V = 18.84 m^3
8) Euler's method for
Current given in the circuit = di/dt = 3 – i/t where t = 1.5 to t = 2.5 in increment of 0.2.
the initial condition given was t =1, i=2
here, f(x) = 3 – i/t
we will replace y = I,
so, i(t) = 3 – i/t
t0 = 1, i0 = 2 and h = 0.2
f(1,2) = 3-i/t
f(0)= f(1,2) = 3-(2/1)
f(0)= 1
y1 = y0+hf0
= 2 + 0.2(1)
= 2.2
function f(1.5,2.2) = f1
= 3-2.2/1.5 = 1.54
y2 = y1 + hf1
= 2.2 + (0.2)*1.54
= 5.28
f2 = f(2.5,5.28)
= 3-5.28/2.5
= 0.88
11

the last equation of euler's method is
y3 = y2 + hf2
= 5.28 + 0.2*0.88
y3 = 5.456
Task 4
9) 60% of adults hold the view;
the random sample of 20 adults were selected; so,
to find out the probability, the formula given here is;
p(x) = (x^n) P^x (1-P)^(n-x)
where, n = fixed number of trials
x = specified number of success
n-x = number of failure
p = probability of success
1-p = probability of given failure (can be noted as q)
n = 7, p = 0.6, then q = 0.4
P(x) = [n ! / x ! (n – x)!] * p^x * q^n-x
a) X = random variables 0,1,2.3
P(0) = [ 7! / 0 ! (7)!] * 0.6^0 * 0.4^ 7
P(0) = 0.00163
similarly we can find out the values for all the random variables,
P(1) = 0.6^1 * 0.4^6
P(1) = 0.00245
so, by the help of binomial probability table, the probability for the number of adults hold the
same opinion after 7 try is 0.5 .
b) n = 13, rest all the values will remain same;
P(0) = [ 13! / 0!* 13!] * 0.6^0 * 0.4 ^ 13
P(0) = 0.000671
same way we will find out the values of other variables also, and those will be
P(1) = 0.6* 0.4^12
P(1) = 0.000166
12

so, by the help of binomial probability table, the number of adults which holds the same opinion
will be = 0.360
c) the values here can be taken from 12 to 15, so we are taking it 13. the calculations will be
same as done above, and the probability will be = 0.360.
10) complaint service average = 3.5
Poisson distribution can be calculated by the given formula
f(x) = (e^-λ) λ^x / x!
Where, λ = average rate of value
X = poisson random variable
e = 2.718
a) the number of complaints received by the company = 0 next week, so X =0
λ = 3.5
therefore, f(x) = (2.718)^-3.5 * 3.5^0 / 0 !
f(x) = 0.0302
so, there are 3% probability that the company will get no complaint next week.
b) x = number of complaints the company will receive during next week,
so, let us assume that the company will receive 4 complaints next week, therefore X = 4;
we will use the same formula for the distribution of probability, i.e.
f(x) = (e^-λ) λ^x / x!
We will vary the value of x from 0 to 4; therefore
f(0) = 0.0302
f(1)= (2.718)^-3.5 * 3.5^1
f(1) = 0.1057
f(2) = (2.718)^-3.5 * 3.5^2 / 2
f(2) = 0.1849
f(3) = (2.718)^-3.5 * 3.5^3 / 3!
f(3) = 0.2158
f(4) = (2.718)^-3.5 * 3.5^4 / 4!
f(4) = 0.1888
13

c) table will looks like this;
x 0 1 2 3 4
f(x) 0.0302 0.1057 0.1849 0.2158 0.1888
n = 5
mean = Σ f(x)/ n
mean = 0.0302+0.1057+0.1849+0.2158+0.1888/5
mean = 0.1450
variance = for that we have to find out Σ f(x)^2 = (0.0302+0.1057+0.1849+0.2158+0.1888)^2
variance = 1/n Σ x^2 f
variance = 1.862
standard deviation = √(1.862)
= 1.3645
mean deviation = Σ ( X – x)/n
where X = reading from table
x = mean
so mean deviation = (8-0.1450)/5
= 1.571
11) find out the regression line;
X = 0 1 2 3 4 5 6 7 8
Y = 2.4 3.8 4.4 2.6 6.8 1.8 6.4 3.6 3.2
for the regression line, we have to find out certain values such as X * Y and X*X
X = 0 1 2 3 4 5 6 7 8
Y = 2.4 3.8 4.4 2.6 6.8 1.8 6.4 3.6 3.2
X^2= 0 1 4 9 16 25 36 49 64
X*Y = 0 3.8 8.8 7.8 27.2 9 38.4 25.2 25.6
we will calculate the sum of each column, and i.e;
Σ X = 36, Σ X^2 = 204, Σ X*Y = 145.8, Σ Y = 35
there is a equation to find out the line, and we will use that equation, which is;
a = (ΣY * Σ X^2 - Σ X * Σ XY) / n . ΣX^2 – (Σ X)^2
a = 35*204 – 36*145.8 / 9*204 – 36^2
a = 3.502
14

similarly, the value of b can be found out as,
b = (n. Σ XY - Σ X . ΣY)/ n . ΣX^2 – (Σ X)^2
b = 9*145.8- 36*35/ 9*204 – 36^2
b = 0.097
the equation of regression line can be given as; y = a+ b. x
So, just substitute the values of a and b in the given equation, and
y = 3.502 + 0.097 . x
12) solution of differential equation;
dy/dx – 4y = 0
i) the general solution =
dy/dx – 4y=0
dy/dx = 4y
therefore, dy/4y = dx
now integrate both the side;
∫ dy/4y= ∫ dx
¼ ∫dy/y = ∫ dx
¼ ln (y) = x + C
we will solve this for equation y;
ln (y) = 4 x+ C
y = (e)^4x+c
y = e^4x . e^C
y = Ce^4x
ii) for particular solution y(0) = 1 and y1(0)= 2
we will just put the limits of y while doing integration;
∫ dy/4y = ∫ dx
¼ ∫ dy/y = x + C
¼ (1-1/2) y = x + C
0.125 y = x + C
15

16