Applied Mathematics for Engineers Assignment (HNCB036) - Solutions

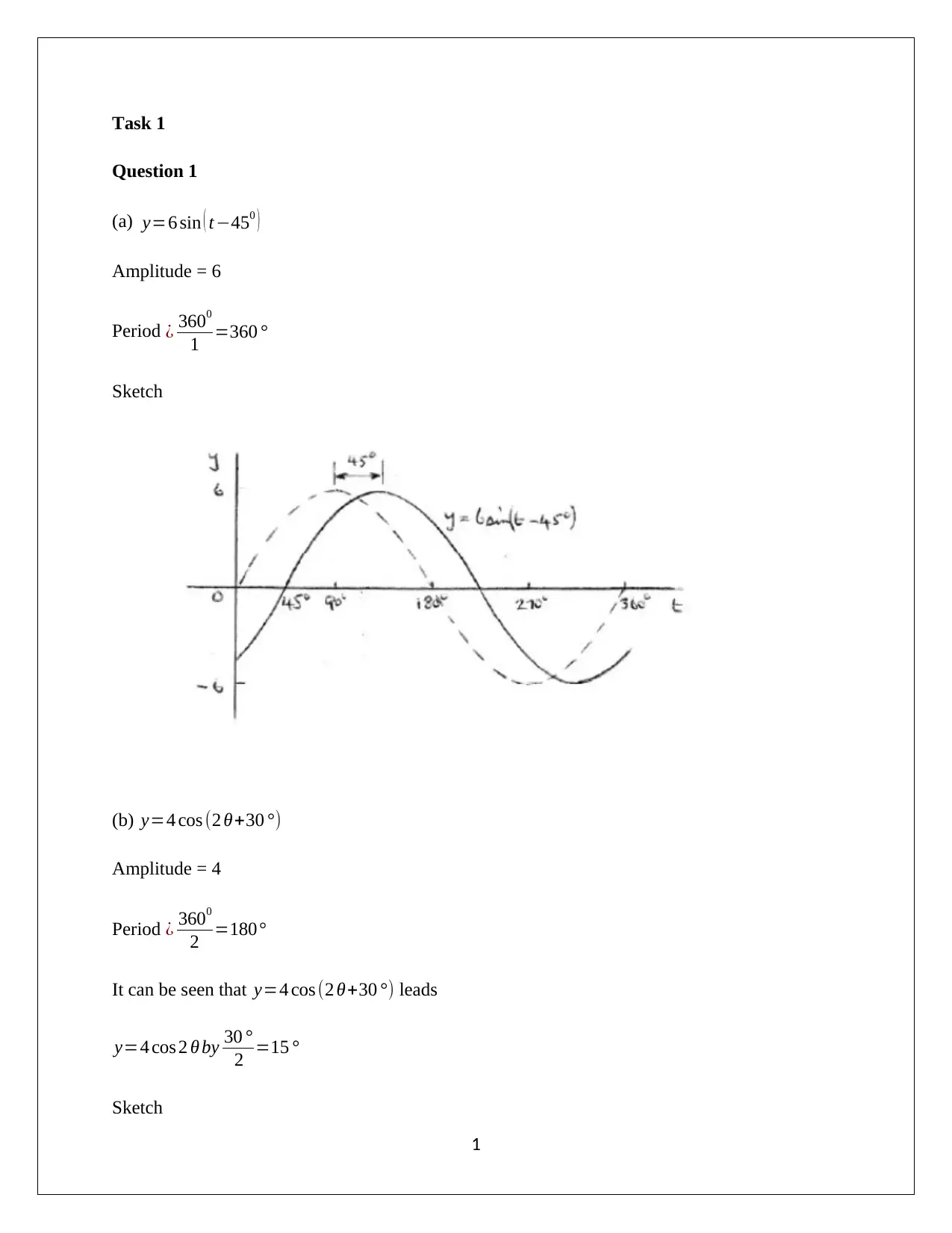
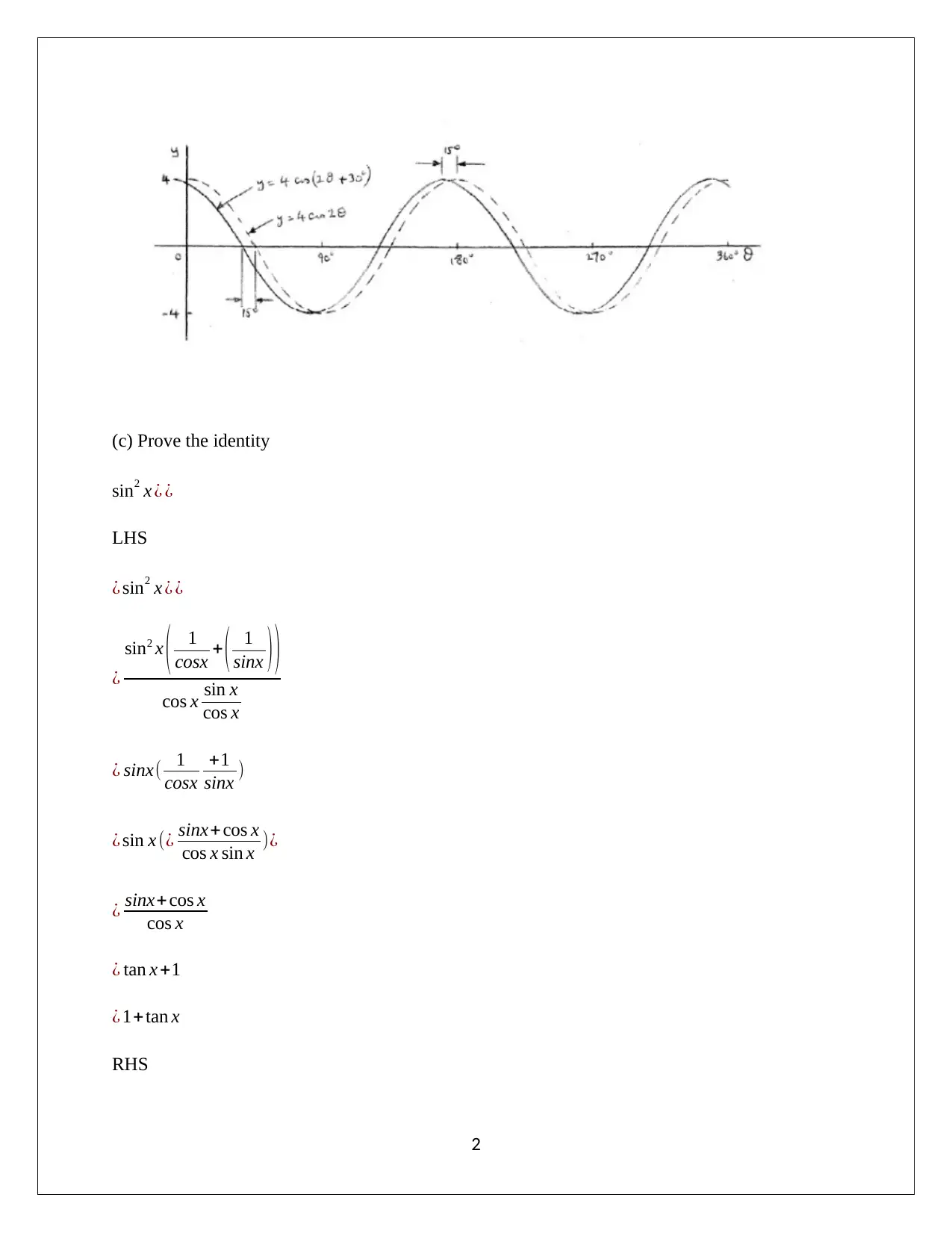
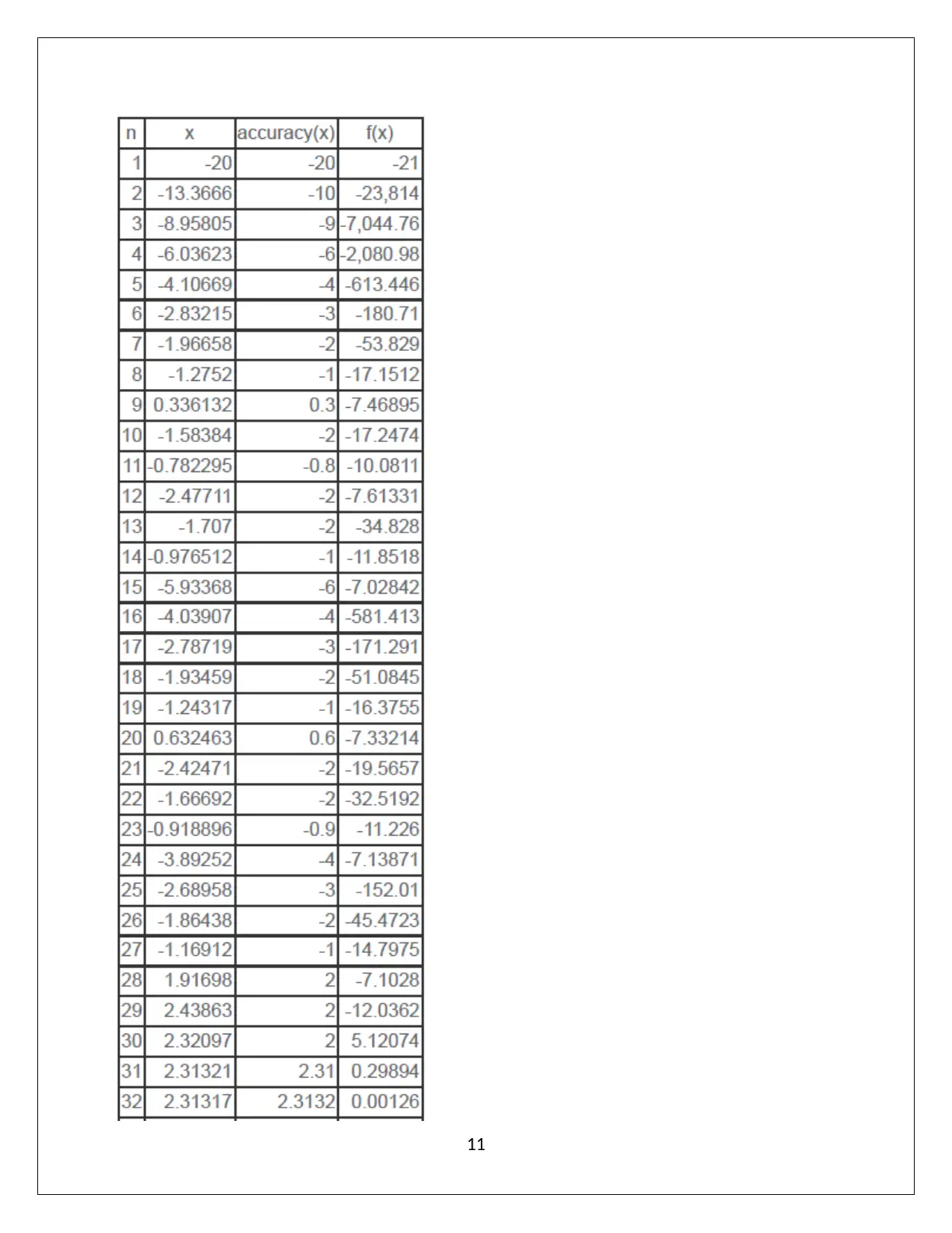
This document presents a comprehensive solution to an Applied Mathematics for Engineers assignment, addressing various mathematical concepts and problem-solving techniques. The assignment covers topics including trigonometric functions, Gaussian elimination, numerical methods (bisection and Newton-Raphson), optimization problems involving surface area and volume, calculus applications such as finding the rate of change of surface area and calculating volumes of revolution, solving differential equations using Euler's method, and statistical concepts like probability distributions (binomial and Poisson) and regression analysis. The solutions are detailed, providing step-by-step explanations and calculations for each problem, making it a valuable resource for students studying applied mathematics.

HNCB036 APPLIED MATHEMATICS FOR ENGINEERS
ASSIGNMENT
Student Name
[Pick the date]

Task 1
Question 1
(a) y=6 sin ( t −450 )
Amplitude = 6
Period ¿ 3600
1 =360 °
Sketch
(b) y=4 cos (2 θ+30 °)
Amplitude = 4
Period ¿ 3600
2 =180°
It can be seen that y=4 cos (2 θ+30 °) leads
y=4 cos 2 θ by 30 °
2 =15 °
Sketch
1

(c) Prove the identity
sin2 x ¿ ¿
LHS
¿ sin2 x ¿ ¿
¿
sin2 x ( 1
cosx + ( 1
sinx ) )
cos x sin x
cos x
¿ sinx( 1
cosx
+1
sinx )
¿ sin x (¿ sinx+ cos x
cos x sin x )¿
¿ sinx+ cos x
cos x
¿ tan x +1
¿ 1+ tan x
RHS
2

¿ 1+ tan x
Hence, the identity is provided LHS =RHS
(d) sin ( x+ π
3 )+sin ( x+ 2 π
3 )= √3 cos x
LHS ¿ {cos ( x )sin ( π
3 ) +cos ( π
3 ) sin ( x ) }+{cos ( x ) sin ( 2 π
3 ) + cos ( 2 π
3 ) sin ( x ) }
Here,
sin(¿ 2 π
3 )= √3
2 ¿
cos ( 2 π
3 ) =−1
2
sin ( π
3 )= √3
2
cos ( π
3 )= 1
2
¿ { √3
2 cos ( x )+ 1
2 sin ( x ) }+ { √3
2 cos ( x )− 1
2 sin ( x ) }
¿ √3
2 cos ( x ) + 1
2 sin ( x ) + √3
2 cos ( x )− 1
2 sin ( x )
¿ 2∗√ 3
2 cos ( x )
¿ √ 3 cos( x )
RHS ¿ √ 3 cos( x )
Hence, the identity is provided LHS =RHS
3

Task 2
Question 2
Gaussian elimination
5 T1 +5 T 2+5 T 3=7
T 1+2 T 2+ 4 T 3=2.4
4 T1 +2 T2 +0 T 3=4
Matrix form
4

Hence,
T 1=0.8
T 2=0.4
T 3=0.2
5

Question 3
x2+ 3 x −5=0
Let
f ( x )=x2 +3 x−5=0
1st iteration
f ( 1 ) =−1<0∧f ( 2 )=5> 0
Roots between 1 and 2
xo= 1+2
2 =1.5
f ( xo ) =f ( 1.5 ) =1.75>0
2nd iteration
f ( 1 ) =−1<0∧f ( 1.5 )=1.75> 0
Roots between 1 and 1.5
x1= 1+1.5
2 =1.25
f ( x1 ) =f ( 1.25 )=0.3125> 0
3rd iteration
f ( 1 ) =−1<0∧f ( 1.25 )=0.3125> 0
Roots between 1 and 1.25
6

x2= 1+1.25
2 =1.125
f ( x2 ) =f ( 1.125 )=−0.35938<0
4th iteration
f ( 1.125 )=−0.35938<0∧f ( 1.25 ) =0.3125>0
Roots between 1.125 and 1.25
x3= 1.125+1.25
2 =1.1875
f ( x3 ) =f ( 1.1875 ) =−0.02734<0
5th iteration
f ( 1.1875 ) =−0.02734< 0∧f ( 1.25 ) =0.3125> 0
Roots between 1.1875 and 1.25
x4 =1.1875+1.25
2 =1.21875
f ( x4 )=f ( 1.21875 ) =0.1416> 0
6th iteration
f ( 1.1875 ) =−0.02734< 0∧f ( 1.21875 ) =0.1416> 0
Roots between 1.1875 and 1.21875
x5= 1.1875+1.21875
2 =1.20312
f ( x5 ) =f ( 1.20312 ) =0.05688> 0
7th iteration
f ( 1.1875 )=−0.02734<0∧f ( 1.20312 )=0.05688>0
7

Roots between 1.1875 and 1.20312
x6= 1.1875+1.20312
2 =1.19531
f ( x6 ) =f ( 1.19531 )=0.01471> 0
8th iteration
f ( 1.1875 )=−0.02734<0∧f ( 1.19531 )=0.01471>0
Roots between 1.1875 and 1.19531
x7= 1.1875+1.19531
2 =1.19141
f ( x7 ) =f ( 1.19141 ) =−0.00633>0
9th iteration
f ( 1.19141 ) =−0.00633<0∧f ( 1.19141 ) =0.01471>0
Roots between 1.19141 and 1.19531
x8= 1.19141+1.19531
2 =1.19336
f ( x8 ) =f ( 1.19336 ) =0.00418>0
10th iteration
f ( 1.19141 ) =−0.00633<0∧f ( 1.19336 ) =0.00418>0
Roots between 1.19141 and 1.19336
x9= 1.19141+ 1.19336
2 =1.19238
f ( x9 ) =f ( 1.19238 ) =−0.00107>0
11th iteration
8

f ( 1.19238 )=−0.00107< 0∧f (1.19336 )=0.00418>0
Roots between 1.19238 and 1.19336
x10=1.19238+1.19336
2 =1.19287
f ( x10 )=f ( 1.19287 )=0.00155>0
12th iteration
f ( 1.19238 )=−0.00107< 0∧f (1.19287 )=0.00155>0
Roots between 1.19238 and 1.19287
x11=1.19238+1.19287
2 =1.19263
f ( x11 )=f ( 1.19263 ) =0.00024 >0
Summary Table
It can be said that the root of the equation x2+3 x −5 using bisection method is 1.19.
Question 4
Critical speed of oscillations = x
9

3 x3−10 x−14
Newton Rapson Method
Let
f ( x )=3 x3−10 x−14
f ' ( x )=9 x2−10
Let the initial guess is x1=1
xn+1=xn − f ( xn)
f ' ( xn )
 n = 1
x1+1=x1− f ( x1 )
f ' (x1 )
x2=1− 3 ( 1 )3− ( 10∗1 )−14
9 ( 1 )2−10 =−20
 n =2 23814
x2+1=x2− f ( x2)
f ' ( x2)
x3=−20−3 (−20 )3− ( 10∗(−20 ) ) −14
9 (−20 )2−10 =−13.34
In a same way, the iteration can be performed and the table is shown below:
10

11