Applied Mathematics: Statistical Inference and Hypothesis Testing

This Applied Mathematics assignment solution demonstrates the computation and interpretation of 95% confidence intervals for control and treatment groups in a medical study, followed by a hypothesis test to evaluate the effectiveness of a drug. It further explores the application of the Chi-Square test to determine the relationship between pulse rate and weight, concluding with probability calculations for medical conditions and an analysis of the significance level's impact on hypothesis testing regarding average systolic pressure. The assignment emphasizes the importance of statistical inference in medical research and decision-making.

APPLIED MATHEMATICS
STUDENT ID:
[Pick the date]

c) i) The objective is to compute the 95% confidence intervals for both groups. This has been
done below.
Group 1: Control group
Mean = 12.2 days
Standard deviation = 1.9 days
Sample size = 45 mice
Standard error = standard deviation / sqrt (sample size) = 1.9/sqrt(45) = 0.283
Degree of freedom = sample size -1 =45-1= 44
The t value for 95% confidence interval = 2.015
Lower limit = Mean – (t value * standard error) = 12.2 – (2.015* 0.283) = 11.63
Upper limit = Mean + (t value * standard error) = 12.2 + (2.015* 0.283) = 12.77
The 95% confidence interval =[ 11.63 12.77]
Group 2: Treatment Group
Mean = 13.60 days
Standard deviation = 1.78 days
Sample size = 9 mice
Standard error = standard deviation / sqrt (sample size) = 1.78/sqrt(9) = 0.595
Degree of freedom = sample size -1 =9 -1 =8
The t value for 95% confidence interval = 2.306
Lower limit = Mean – (t value * standard error) = 13.6-(2.306*0.595)= 12.23
Upper limit = Mean + (t value * standard error= 13.6+(2.306*0.595)= 14.97
The 95% confidence interval =[ 12.23 14.97]

ii) The above confidence intervals for the mean paralysis time for the control group and
treatment group ought to be compared so as to opine if the drug had an effect.
Null Hypothesis: The drug did not have any effect as the confidence intervals of the two
groups overlapped.
Alternative Hypothesis: The drug did have some effect as the confidence intervals of the two
groups did not overlap.
It is apparent that the mean paralysis time confidence intervals for the two groups does
overlap owing to which it cannot be concluded that the mean paralysis time would differ
significantly. Hence, it can be concluded that the drug is not effective.
a) i) The correct statement is A while the other two statements are incorrect.
ii) A – T statistic
B- F statistic
C – Chi Square statistic
b) Hypothesis test needs to be conducted in the given case. The requisite hypotheses are as
indicated below.
Null Hypothesis: There is no significant relationship between pulse rate and weight and
hence the two variables are independent.
Alternative Hypothesis: There is significant relationship between pulse rate and weight and
hence the two variables are dependent.
The assumed level of significance is 5%
The computations for Chi Square Test are highlighted as follows.

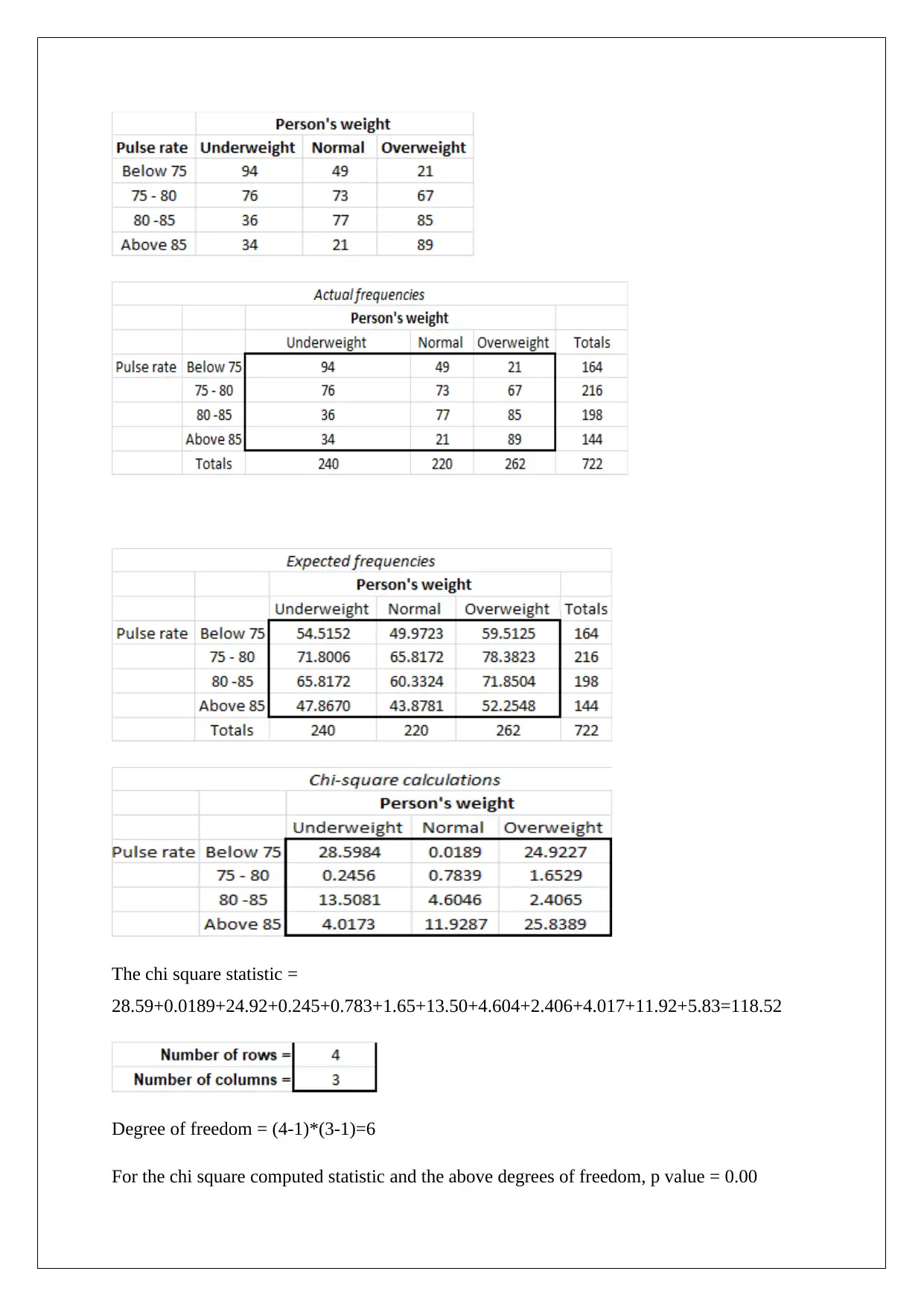
The chi square statistic =
28.59+0.0189+24.92+0.245+0.783+1.65+13.50+4.604+2.406+4.017+11.92+5.83=118.52
Degree of freedom = (4-1)*(3-1)=6
For the chi square computed statistic and the above degrees of freedom, p value = 0.00

As the p value is lower than the assumed significance level, hence it can be concluded that
the null hypothesis would be rejected and alternative hypothesis would be selected. Thus, it
may be correct to conclude that the pulse rate and weight are dependent on each other and not
independent of each other.
a) The second law of probability would be useful in this case as it states the underlying of
occurrence of independent events is essentially the product of the respective probabilities of
these different events.
Based, on the given information, probability of being affected by the condition = (1/100) =
0.01
Hence, probability of not being affected = 1-0.01 = 0.99
Probability that only 1 of the 5 patients have the condition = 5C1*(0.01)*(0.99)4 = 0.04803
Probability that atleast 1 out of 5 patients have the condition = 1- P(No patient having the
condition) = 1-(0.99)5 = 1-0.95099 = 0.04901
b) The applicability of the given statistical analysis would be dependent on the underlying
significance level which has been assumed for the study. Considering the objective of the
study, the following would be the underlying hypothesis that would have been utilised.
Null Hypothesis: Average systolic pressure is less than or equal to 140 mm Hg
Alternative Hypothesis: Average systolic pressure is greater than 140 mm Hg
It is known that p value came out as 0.07. The decision rule is that null hypothesis is rejected
only when the p value tends to be lower than the level of significance. Hence, if level of
significance is lower than 7%, then the null hypothesis is not rejected and hence the
conclusion drawn is that the average systolic pressure is lower than or equal to 140 mm Hg.
However, if the level of significance is greater than 7%, then there would be rejection of null
hypothesis and conclusion that the claim regarding average systolic pressure exceeding 140
mmHg is correct.