BTEC L3 Applied Science: Mathematical Calculations for Science

This assignment focuses on mathematical calculations for applied science, covering several key areas. It begins with logarithms and indices, solving problems involving exponential expressions and logarithmic equations. The assignment then moves to logarithms and algebra, including factorization and solving simultaneous and quadratic equations. Calculus is addressed with tasks on differentiation and integration, including finding gradients and areas under curves. Finally, the assignment covers circular measure and trigonometry, converting between degrees and radians and solving trigonometric problems. The document provides detailed solutions and explanations for each task.

APPLIED SCIENCE
1 | P a g e
Mathematical Calculations for Science

APPLIED SCIENCE
Contents
Logarithms and Indices –.................................................................................................................3
Task-1 Solution............................................................................................................................3
Task-2 Solution............................................................................................................................5
Logarithms and Algebra-.................................................................................................................6
Task-1, Solution...........................................................................................................................6
Task-2, Solution...........................................................................................................................9
Differentiation and integration-.....................................................................................................10
Task-1, Solution.........................................................................................................................10
Task-2, Solution.........................................................................................................................13
Circular measure and trigonometry –............................................................................................15
Task-1 Solution..........................................................................................................................15
Task-2 Solution..........................................................................................................................16
Task-3- Solution........................................................................................................................17
Task 4- Solution.........................................................................................................................18
References......................................................................................................................................20
2 | P a g e

APPLIED SCIENCE
Logarithms and Indices –
Task-1 Solution
1a) C2 x C3 (On multiplication power are added for same base)
⇒ C2+3=C5 Ans
1b) b3 x b4 xb5 (On multiplication power are added for same base)
b3+4 +5=b9 Ans
1c) ( a2 )3 (On power of the power is multiplied)
( a2 x 3 )=a5 Ans
1d) m7
m3 (Power is subtracted on division)
( m7−3 ) =m4 Ans
1e) ( 5 a3 b c4 )2 (On power of the power is multiplied)
25 a3 x2 b1 x2 c4 x2 =25 a6 b2 c8 Ans
1f) p−3 q2 (The negative power goes to the denominator)
q2
p3 Ans
1g) ( b2
c4 )
3
(On power of the power is multiplied)
b2 x3
c4 x3 = b6
c12 =b6 .c−12 Ans
3 | P a g e

APPLIED SCIENCE
2. considering base 10 for given logarithm
2a) log8 + log6
Log is multiplied when it is in addition form
Log8 +log6 = log48 = 1.68124. Ans
2b) log8 -log6
Log is divided when it is in subtraction form.
Log8 – log6 ¿ log ( 8
6 ) = log1.33 = 0.12483 Ans
2c) log (8)c =
Log is multiplied when it is in power form.
log (8)c = c.log (8) = 0.90308C Ans
3) Solution
3a) 102x = 320.2 (Taking log on both side)
log102x = log320.2
then, 2x = 2.5054, then x = 1.2527 Ans
3b) b.3.1x = 80 where b = 8
Taking log from both side
Logb.3.1x = log80
Logb + xlog3.1 = log 80 (putting the value of b and taking log value of 8 and 80)
Log8 + xlog3.1 = log80
4 | P a g e

APPLIED SCIENCE
X x 0.491 = 1.9030 – 0.9030
X = 2.036 Ans
3c) logx3 = 9
As per logarithm rule,
Logx3 = 9
⟹ 3 logx=9
⟹ logx=3
⟹ x=103 or x = 1000 Ans
Task-2 Solution
1) As given in question,
T = 27.3 days, G = 6.67 x 10-11 Nm2kg-2, M = 5.975 x 1024 kg
R =?
As per given formula,
T = √ 4 π2 r3
GM (Giving power on both side by 2
T 2= 4 π2 r3
GM
⇒ T2 GM
4 π2 =r3 or, ⇒ r3 = ( 27.3 x 24 ) 2 x 6.67 x 10−11 x 50975 x 1024
4 x 3.14 x 3.14
5 | P a g e

APPLIED SCIENCE
⇒ r3 = ( 27.3∗24∗60∗60 )2 x 6.67 x 10−11 x 50975 x 1024
4 x 3.14 x 3.14
⇒ r3 =5.622 x 1025 , ⇒ r =3
√5.622 x 1025= 383088467.7 m = 3.83 x 108 m Ans
2) As given in question,
ρ=1 x 105, V = 7x10-5 m3, m = 6.6 x 10-27 and N = 2 x 1022 atoms
a) As per given equation,
pV =⅓ Nm c2
3 pV
Nm =c2
Putting the value in above equation
c2= 3 x 105 x 7 x 10−5
2 x 1022 x 6.6 x 10−27
⇒ c2= 21
0.00132 =159090.909 m2 s−2
Mean square speed = 159090.909 m2 s−2
b) As given in question,
r . m. s . speed= √c2 Putting the value from previous solution
r . m. s . speed= √159090.909=398.862m/s Ans
Logarithms and Algebra-
Task-1, Solution
6 | P a g e

APPLIED SCIENCE
1. The factorization is as follows
a) 4x -6xy
= 2(2x-3xy) = 2x(2-3y) Ans
b) 2abc-6abd
= 2(abc-3abd) = 2ab(c-d) Ans
c) 4(a-b) – c(a-b), Taking common (a-b) from both equation
= (a-b) (4-c) Ans
d) 2pr-4ps+qr-2qs
= 2pr+qr -4ps-2qs Arranging
= r(2p+q) -2s(2p+q) Taking common (p+q)
= 2(2p+q) (r-2s) Ans
2. The factorization is as follows
a) x2 -5x+4
= x2 -4x – x +4 (splitting the middle part in suitable addition)
= x(x-4) -1(x-4) (Taking common as (x-4)
= (x-1) (x-4) Ans
b) 4x2 – 36 (We know that, a2 – b2 =(a-b) (a+b))
= (2x-6) (2x+6) Ans
c) X2 -4x +4
= x2 -2x-2x + 4
= x(x-2) -2(x-2) = (x-2) (x-2) = (x-2)2 Ans
d) 3x2 – 5x-28 (splitting the middle part in suitable addition)
= 3x2 – 12x+7x-28
= 3x(x-4) 7(x-4) = (3x-7) (x-4) Ans
7 | P a g e

APPLIED SCIENCE
3. The The solution is as follows
a) 5x -7y=1 ………(i)
2x+5y = 21 ……. (ii)
Multiplying equation (i) x 5 and (ii) with 7
25x – 35y = 5
14x + 35y = 147 By adding both the equation
39x = 152, x = 152/39 = 3.8974
Putting the value of x and solving 7y = 18.48717, y = 2.641 Ans
b) Y = 5x +4 ……….(i)
Y = 4x+6 ……….(ii)
Equating both the equation,
5x+4 = 4x+6
= 5x -4x = 6-4
x = 2
Putting the value of x in equation (i)
Y = 5*2 +4 = 14
Therebefore, x = 2 and y = 14
4. The solution of quadratic equation is as follows
a) 3x2 -7x +2 = 0
= 3x2 -6x -x +2
= 3x(x-2) -1(x-2) = (3x-1) (x-2) Ans
b) 2x2 -9x +7
= 2x2 – 7x-2x+7
= x(2x-7)-1(x-7)
8 | P a g e

APPLIED SCIENCE
= (x-1) (2x-7) Ans
c) 10x2 +5x-15
= 10x2 + 5x -15
= 10x2 +15x -10x -15
= 5x(2x+3) -5(2x+3)
=(5x-5) (2x+3) Ans
Task-2, Solution
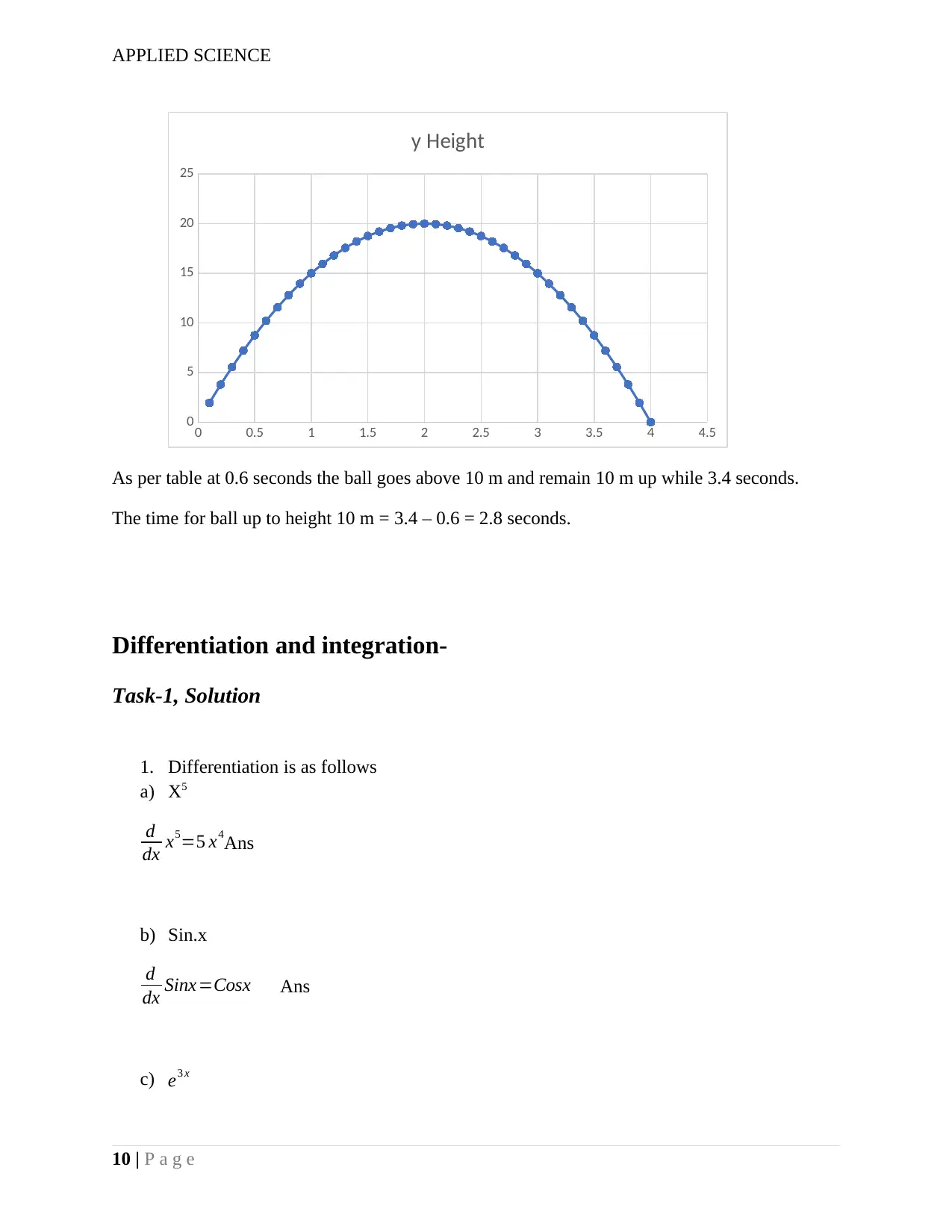
1) For the given problem, we have to construct table for value of y at a given time t, we
have to draw graph and find out the solution.
As given in question,
Y = 20t – 5t2 . Putting the different value of t we will get different value of y
t y t y t t y
0.1 1.95 1.1 15.95 2.1 19.95 3.1 13.95
0.2 3.8 1.2 16.8 2.2 19.8 3.2 12.8
0.3 5.55 1.3 17.55 2.3 19.55 3.3 11.55
0.4 7.2 1.4 18.2 2.4 19.2 3.4 10.2
0.5 8.75 1.5 18.75 2.5 18.75 3.5 8.75
0.6 10.2 1.6 19.2 2.6 18.2 3.6 7.2
0.7 11.55 1.7 19.55 2.7 17.55 3.7 5.55
0.8 12.8 1.8 19.8 2.8 16.8 3.8 3.8
0.9 13.95 1.9 19.95 2.9 15.95 3.9 1.95
1 15 2 20 3 15 4 0
If we draw the graph for t verses y we will get like this
9 | P a g e

APPLIED SCIENCE
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
0
5
10
15
20
25
y Height
As per table at 0.6 seconds the ball goes above 10 m and remain 10 m up while 3.4 seconds.
The time for ball up to height 10 m = 3.4 – 0.6 = 2.8 seconds.
Differentiation and integration-
Task-1, Solution
1. Differentiation is as follows
a) X5
d
dx x5=5 x4Ans
b) Sin.x
d
dx Sinx=Cosx Ans
c) e3 x
10 | P a g e

APPLIED SCIENCE
d
dx e3 x= d
dx e3 x . d
dx 3 x=e3 x .3=3 e3 x Ans
d) Lnx
d
dx lnx= 1
x Ans
e) X4
d
dx x−4 =−4 x−5 Ans
f) Cosx
d
dx Cosx=−Sinx Ans
2 Integration is as follows
a) e5x
∫ e5 x=1
5 e5 x+ C Ans
b) Sinx
∫ Sinx=−Cosx+C Ans
c) x7
∫ X7= X7+ 1
7 +1 =¿ x8
8 +C ¿ Ans
d) √ x
11 | P a g e

APPLIED SCIENCE
∫ √ x= x
1
2 +1
1
2 +1
= x3 /2
3
2
= 2
3 x3 /2 +C Ans
e) x-3
∫ X−3= X−3 +1
−3+1 =¿ x−2
−2 = −1
2 x2 +C ¿ Ans
h) 5
x
∫ 5
x =5∫ 1
x =¿ 5 ln |x|+C Ans
3. To find the gradient first I must do derivative of the equation
Y = x3
dy
dx =3 x2 (Putting the value x =2)
dy
dx (At x=2)=3. 22=12
The gradient of the curve = 12 Ans
4. as given equation x = t3 -2t2 +3t -4 where x is the distance and t is the time
The velocity can be given by differentiating the equation
dx
dt =3 t2−4 t+ 3
Putting the value t =4 sec
12 | P a g e