AQM Assignment 2: Statistical Techniques and Probability Analysis

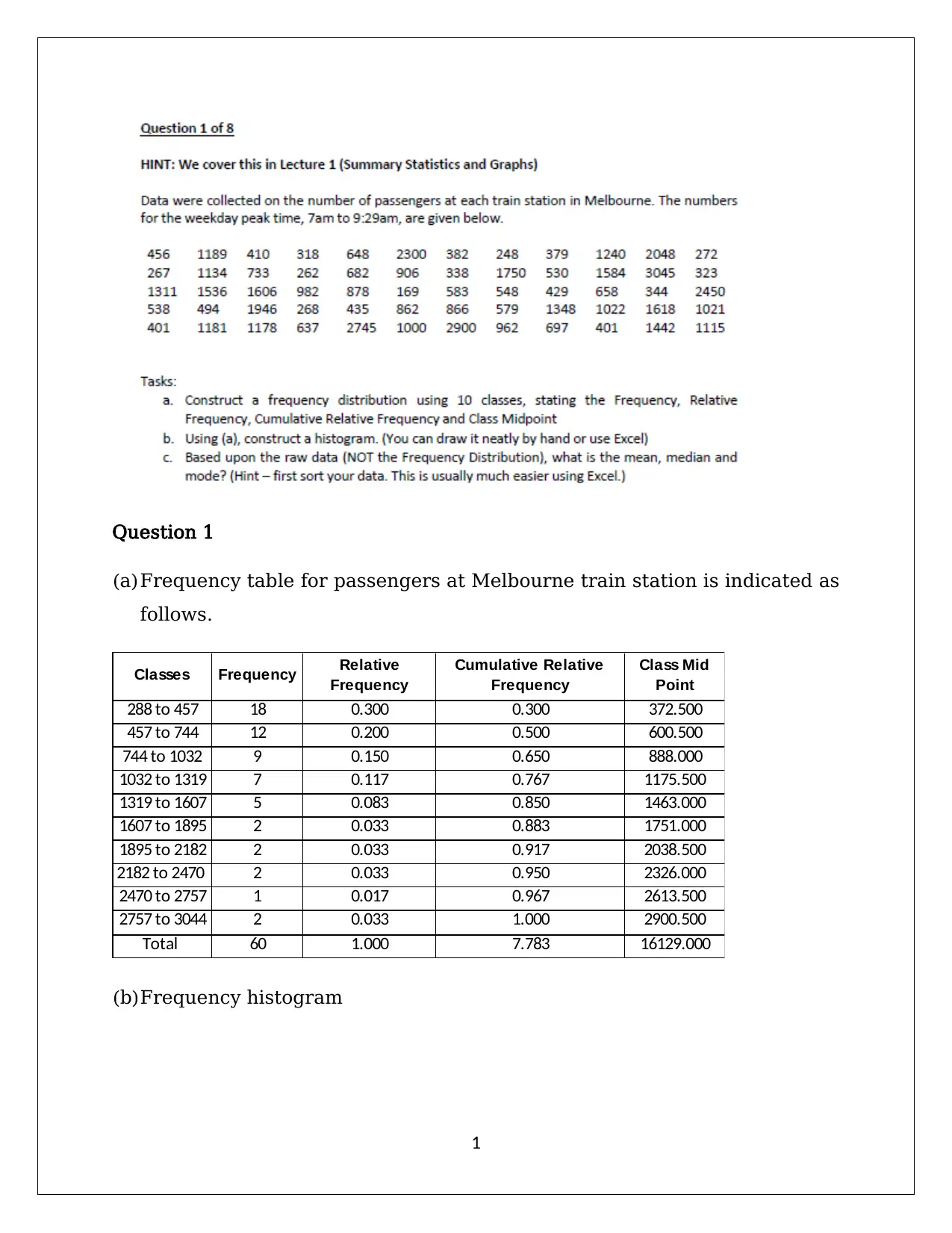
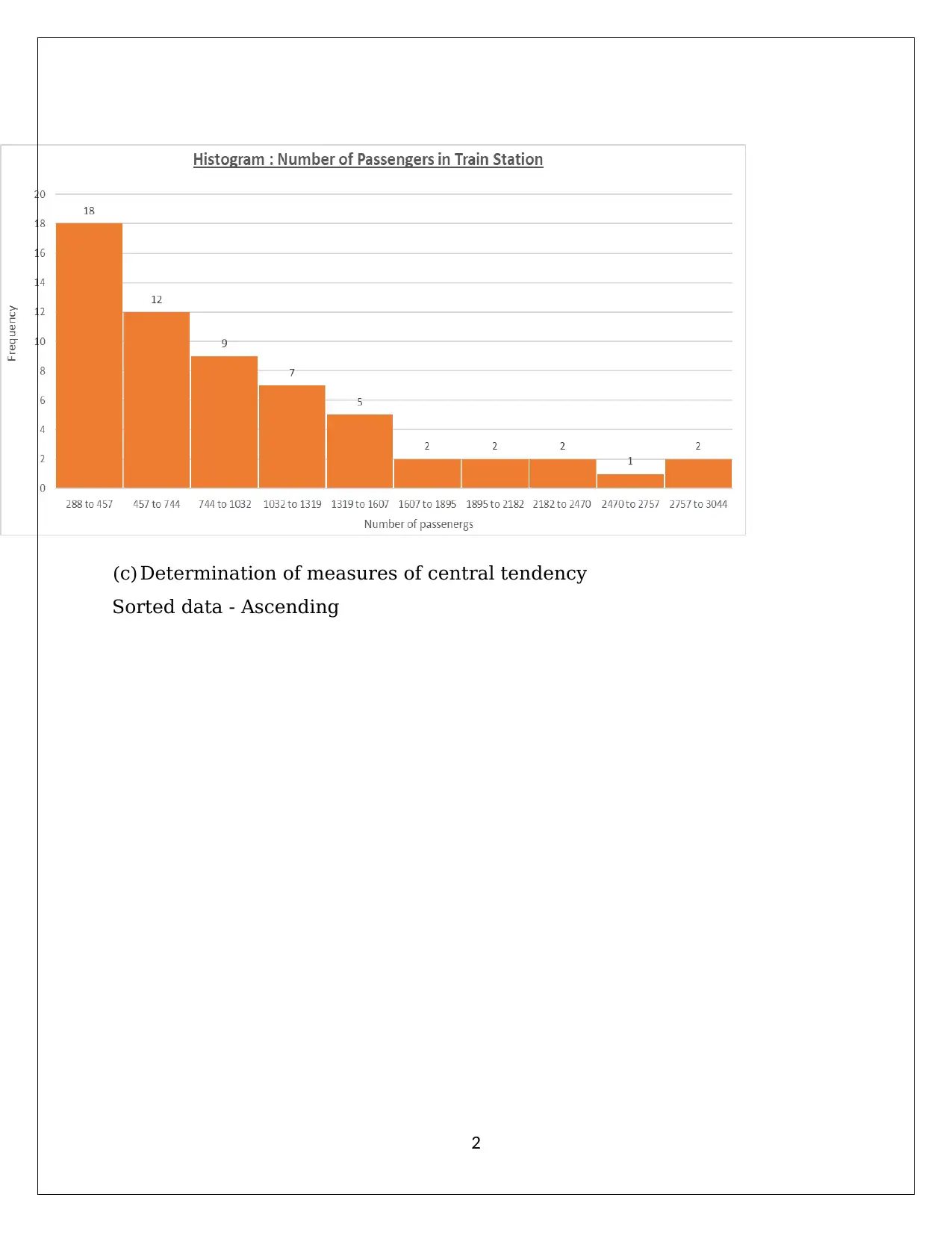
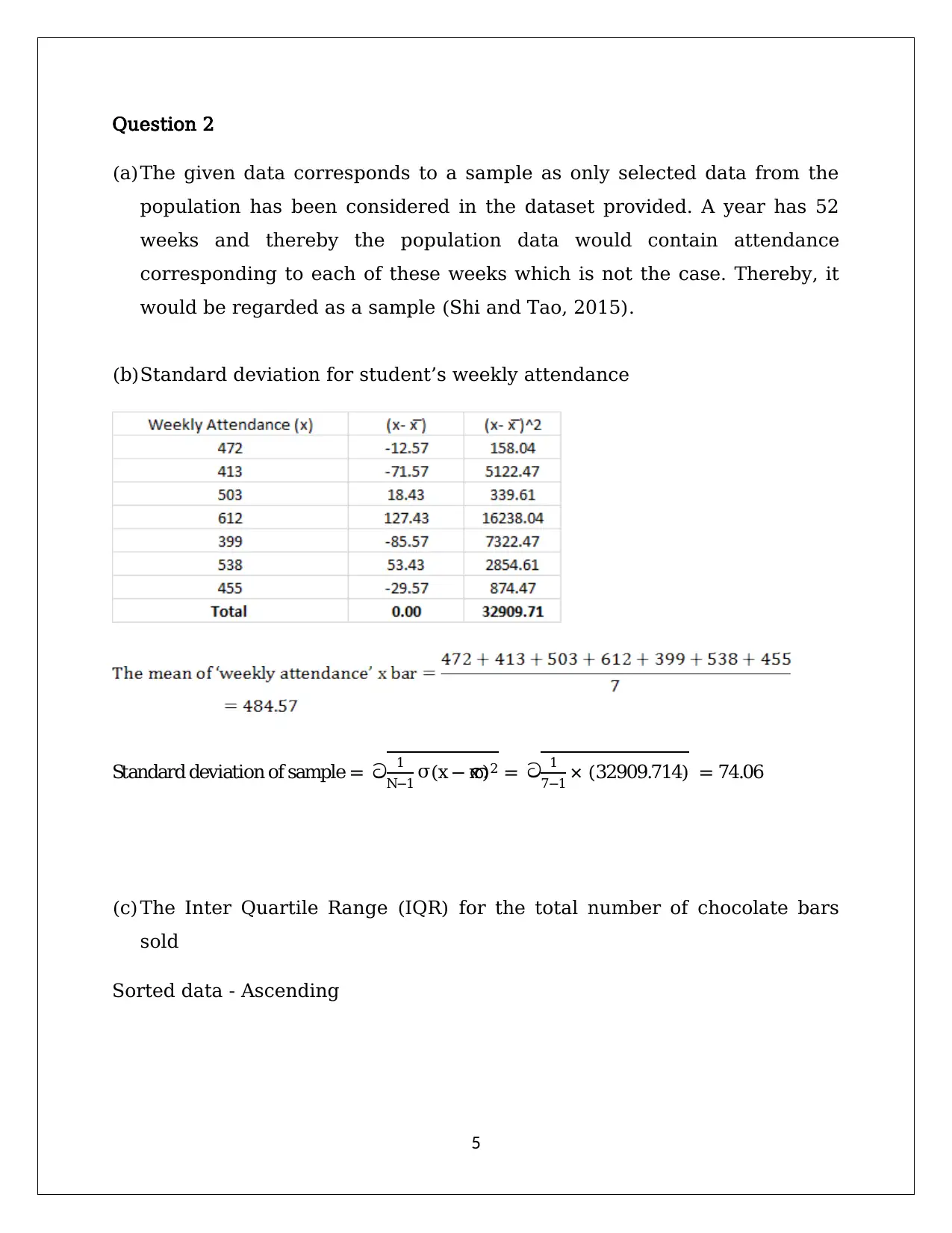
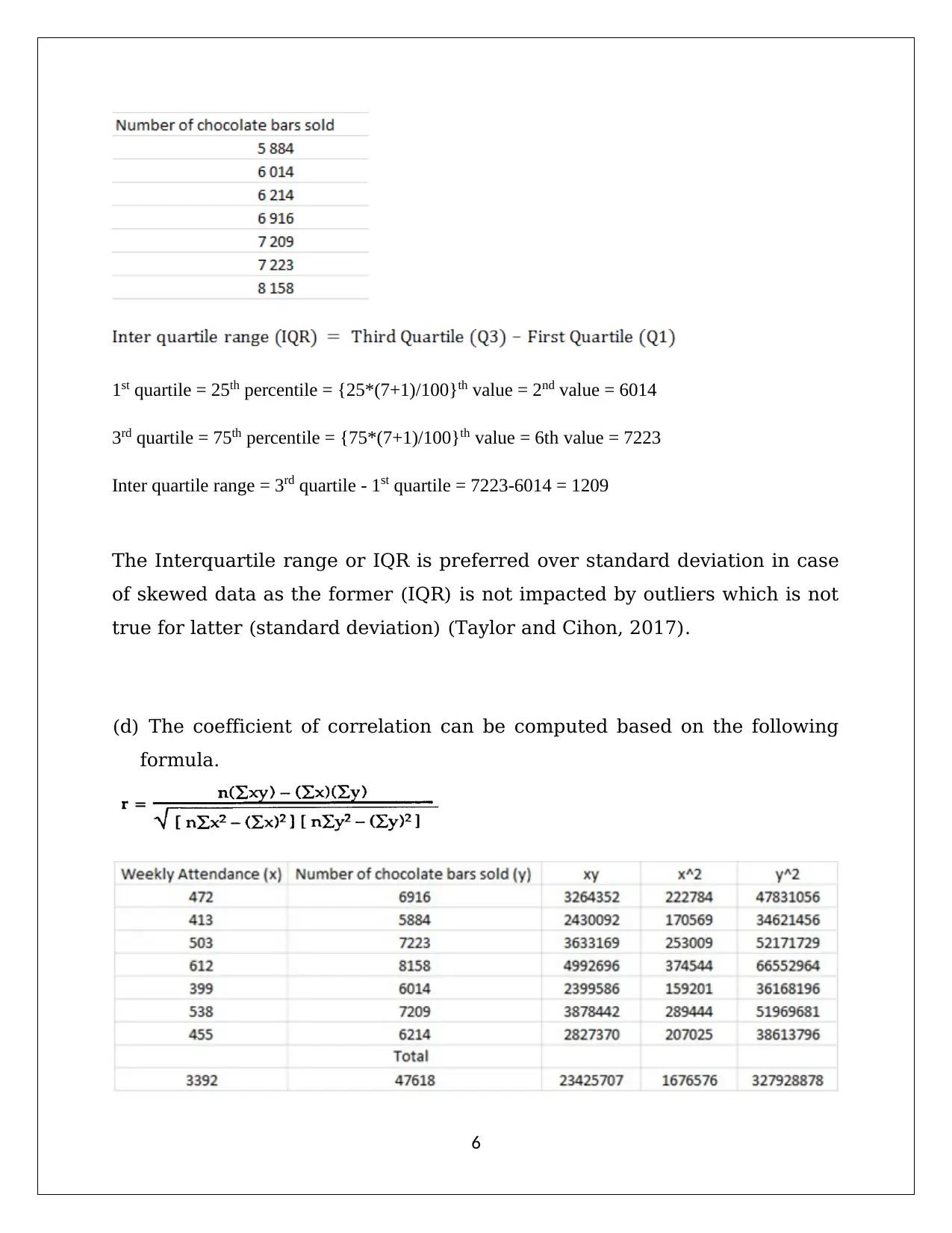
This document presents a comprehensive solution to Applied Quantitative Methods Assignment 2, focusing on statistical analysis and probability. The solution includes detailed calculations and explanations for various statistical concepts. It begins with frequency tables and histograms to analyze passenger data, followed by measures of central tendency. The assignment then delves into sample vs. population, standard deviation, and interquartile range. Correlation analysis and regression equations are derived to examine relationships between variables. Probability concepts are addressed through various scenarios, including independent events, binomial and Poisson distributions, and normal distributions. Hypothesis testing and the Central Limit Theorem are also explored. The document provides clear step-by-step solutions, making it a valuable resource for students studying statistics and quantitative methods. The assignment covers topics such as frequency distribution, measures of central tendency, standard deviation, interquartile range, correlation, regression analysis, probability calculations, binomial distribution, and normal distribution.

APPLIED QUANTITATIVE METHODS
ASSIGNMENT 2
Student Name
[Pick the date]

Question 1
(a)Frequency table for passengers at Melbourne train station is indicated as
follows.
288 to 457 18 0.300 0.300 372.500
457 to 744 12 0.200 0.500 600.500
744 to 1032 9 0.150 0.650 888.000
1032 to 1319 7 0.117 0.767 1175.500
1319 to 1607 5 0.083 0.850 1463.000
1607 to 1895 2 0.033 0.883 1751.000
1895 to 2182 2 0.033 0.917 2038.500
2182 to 2470 2 0.033 0.950 2326.000
2470 to 2757 1 0.017 0.967 2613.500
2757 to 3044 2 0.033 1.000 2900.500
Total 60 1.000 7.783 16129.000
Classes Frequency Relative
Frequency
Cumulative Relative
Frequency
Class Mid
Point
(b)Frequency histogram
1

(c)Determination of measures of central tendency
Sorted data - Ascending
2

3

Sample size = 60
Sum of data values = 58594
Mean = 58594/60 = 976.57
= (733+862)/2 = 797.5
Maximum frequency has observed for 401 and thus, mode would be 401.
4

Question 2
(a)The given data corresponds to a sample as only selected data from the
population has been considered in the dataset provided. A year has 52
weeks and thereby the population data would contain attendance
corresponding to each of these weeks which is not the case. Thereby, it
would be regarded as a sample (Shi and Tao, 2015).
(b)Standard deviation for student’s weekly attendance
Standard deviation of sample = ට 1
N−1 σ(x − xത)2 = ට 1
7−1 × (32909.714) = 74.06
(c)The Inter Quartile Range (IQR) for the total number of chocolate bars
sold
Sorted data - Ascending
5

1st quartile = 25th percentile = {25*(7+1)/100}th value = 2nd value = 6014
3rd quartile = 75th percentile = {75*(7+1)/100}th value = 6th value = 7223
Inter quartile range = 3rd quartile - 1st quartile = 7223-6014 = 1209
The Interquartile range or IQR is preferred over standard deviation in case
of skewed data as the former (IQR) is not impacted by outliers which is not
true for latter (standard deviation) (Taylor and Cihon, 2017).
(d) The coefficient of correlation can be computed based on the following
formula.
6

Variables are strongly correlated in a positive manner because the r value is
not only positive but also significantly high and close to 1 (Hastie, Tibshirani
and Friedman, 2014).
Question 3
7

(a)Regression line
Least Square Regression Equation
Y = a+bX, where, a = intercept and b = slope
a = ቈ
ሼሺ47618ሻ∗ሺ1676576ሻሽ− ሼሺ3392ሻ∗ሺ23425707ሻሽ
{(7 ∗ሺ1676576ሻ) 2 − ሺ3392ሻ2} ቉ = 1628.68
b = ቊ
ሼ7 ∗ሺ23425707ሻሽ− {ሺ3392ሻ∗ሺ47618ሻ}
{(7 ∗(1676576)) 2 − ሺ3392ሻ2} ቋ = 10.677
Regression equation
y = 1628.689 +10.67 x
Number of chocolate bars sold = 1628.689 + (10.67* Weekly attendance)
For the above regression equation, the intercept value is approximately
1629. This would imply that this is the expected weekly sales of chocolate
8

when weekly attendance is zero. The slope coefficient is 10.67 which
implies that a unit change in the weekly attendance would alter tha number
of chocolate bars sale by 10.67 units. Both the given variables would change
in the same direction as slope is positive (Medhi, 2016).
(b)R square
R square = (
R2 = (0.9680)2 = 0.9370
93.7% of the changes in chocolate bars sold will be explained by changes in
weekly attendance of student.
9

Question 4
(a) P (Holmes OR Grassroots)
10

= 35 + 92 + 12
35 + 92 + 54 + 12 = 0.7202
(b) P (External AND Scientific)
= 54
35 + 92 + 54 + 12 = 0.2798
(c) P (Holmes AND Scientific)
= 35
35 + 92 = 0.2756
(d) Training is event X and Recruitment is event Y will be independent
events when
P ሺXሻ.P ሺYሻ= P ሺX AND Yሻ
PሺXሻ= 54 + 12
35 + 92 + 54 + 12 = 0.3412
P ሺYሻ= 35 + 54
35 + 92 + 54 + 12 = 0.4611
P ሺXሻ.P ሺYሻ= 0.3412 ∗0.4611 = 0.1573
P ሺX AND Yሻ= 0.2576
P(X). P(Y) is not same as P (X and Y) which means “Training and
Recruitment” will not be termed as independent events.
11

Question 5
(a) Probability (segment A | product X)
12

(b) Probability that the selected product will be X
13

Question 6
14

(a)Binomial distribution
P ሺx < = 2ሻ= Pሺx = 2ሻ+ P ሺx = 1ሻ+ P (x = 0)
Total trials = 8
The probability of success = 0.1
Pሺx = 2ሻ= {ቀ8
2ቁ ሺ0.1)2ሺ0.9ሻ6ሽ= 0.1488
P ሺx = 1ሻ= {ቀ8
1ቁ ሺ0.1)1ሺ0.9ሻ7ሽ= 0.3826
P ሺx = 0ሻ= {ቀ8
0ቁ ሺ0.1)0ሺ0.9ሻ8ሽ= 0.4304
P ሺx < = 2ሻ= 0.1488 + 0.3826 + 0.4304 = 0.9619
Probability (2 or/less than 2 would buy from shop is 0.9619.
(b)Poisson distribution
P (x) = e−γγx
x!
x = 9
γ = 8
P ሺx = 9ሻ= e−889
(9)!
P ሺx = 9ሻ= 0.124
Probability (9 customers would enter into shop in 2 min) is 0.124.
15

Question 7
(a)Probability (X > $2 million)
(b)Probability ($1 mn < X< $1.1 mn)
16

P (1000000 < x < 1100000)
= P ൬
1000000 − 1100000
385000 < x − μ
σ < 1100000 − 1100000
385000 ൰
= P( −0.26 < z < 0)
From z table
P ሺz < −0.26ሻ= 0.3975
P ሺz < 0ሻ= 0.5
P ሺ1000000 < x < 1100000ሻ= 0.5 − 0.3975 = 0.1025
17

Question 8
(a)The key aspect is that the sample size is 50. This is quite significant as
Central Limit Theorem states that a sample distribution can be assumed
to normal when the sample size is sufficiently large. The minimum
number is taken 30 and hence the given number sample of 50
observations would be sufficient to assume the given distribution as
normal (Hillier, 2016).
(b)P(p>0.30) =?
Proportion of sample p = 11 / 45 = 0.24
Standard error of proportion of sample = ට(1−p)p
n = ට0.24ሺ1−0.24ሻ
45 = 0.064
P ሺp > 30%ሻ= P ൬z > 0.3 − 0.24
0.064 ൰
P ሺp > 30%ሻ= P(z > 0.87)
P ሺz > 0.87ሻ= 0.192
Probability ሺp > 30%ሻ= 0.192
18