Building Mathematics 1: Comprehensive Mathematical Applications

This assignment provides detailed solutions to various mathematical problems under the title Building Mathematics 1. It covers scenarios involving calculations of area, forfeits, conversions, and unit analysis. The assignment also delves into arithmetic and geometric progressions, solving logarithmic and hyperbolic equations. Furthermore, it includes statistical analysis, such as determining mode, median, interquartile range, and standard deviation from revenue data. The assignment also addresses normal distribution, replacement intervals for light bulbs, and hypothesis testing using tailed tests. Desklib is a valuable resource for students seeking similar solved assignments and study materials.

Building Mathematics
1

TABLE OF CONTENTS
Table of Contents.............................................................................................................................1
TASK 1............................................................................................................................................2
Scenario 1....................................................................................................................................2
Scenario 2....................................................................................................................................2
Scenario 3....................................................................................................................................3
TASK 2............................................................................................................................................6
Scenario 1....................................................................................................................................6
Scenario 2..................................................................................................................................10
TASK 3..........................................................................................................................................15
Scenario 1..................................................................................................................................15
Scenario 2..................................................................................................................................18
TASK 4..........................................................................................................................................21
Scenario 1..................................................................................................................................21
Scenario 2..................................................................................................................................23
Scenario 3..................................................................................................................................25
Scenario 4..................................................................................................................................26
2

TASK 1
Scenario 1
(a) Length and width of rectangle
Solution
Area = Lb = 26.5 m2
Where L is length and b is width
Given b = L – 3.2
L*(L – 3.2) = 26.5
L2 – 3.2L -265 = 0
L = { - (-3.2) +- √ [(-3.2)2- 4*1* (26.5)] } / 2*1
L = 6.99 and l = -3.79
AS L cannot be negative so neglecting negative value
Length = 6.990 m
b = 6.99-3.2 = 3.790 m
(a) Daily Forfeit
Solution
Let forfeit amount of one day is = £v and original amount of contract = £u
If there is delay of 5 days, then total amount which will be deducted from contract amount is £5v
Amount received by contract if there is delay of 5 days is expressed as:
u – 5v = £4250
Similarly, if there is 12 day delay then forfeit amount for 12 days = £12v
Amount received by contract:
u – 12v = £2120
On solving both equations:
u – 5v = £4250 (i)
u – 12v = £2120 (ii)
On subtracting both the equations we have:
7v = 2130
v = £304.28
On substituting this value in equation 1
3

u – 5(304.28) = £4250
u = £5771.4
Contract amount u = £5771.4
Forfeit v = £304.28
Scenario 2
(a) Conversions
Solution
Speed = 65 miles per hour
(i) Speed in m/s :
1 mile = 1609.344 meter
1 hour = 3600 seconds so for converting mile/hour into meter/ second * by (1609.344/3600)
65 * 0.44704 = 29.05 meter per second
(ii) Time to cover distance of 100 miles:
Solution
Time = distance/ speed
= 100/65 = 1 hour 53 minutes
For covering distance of 100 miles nearly 1 hour and 53 minutes will be needed.
(iii) Average fuel consumption = 30 miles per gallon
Solution
30 miles per gallon to litre per kilometre:
1 Mile per gallon = 2.35 litre per km
30 miles/ gallon = 30 * 2.35 = 70.5 litre / km
(iv) Fuel required for the journey in litters
Solution
Fuel required for 1 km = 70.5 litre
Total journey 100 miles = 160 km
So fuel required for journey = 11280 litre
4

(a) Unit of lift
Solution
Lift = k *V2 * A * p
A = area = m2 = [M0L2T0]
p = air density = kg / m3 = [M1L-3T0]
k is dimensionless as its constant so = [M0L0T0]
V is speed in m/second = [M0L1T-1]
So V2 = [M0L2T-2]
Lift = [M0L2T0] * [M1L-3T0] * [M0L0T0] * [M0L2T-2]
Lift = [M1L1T-2] = kg meter/ second2
Scenario 3
(1) Arithmetic sequence
Solution
b , 2b/3 , b/3 , 0 .....
Sixth term:
First term a = b
Common difference d = 2b/3 – b = - b/3
Sixth term = a + (n-1) *d
= b + 5(-b/3)
= b – 5b/3
= -2b/3
Sixth term = -2b/3
Kth term : a + (k -1) *d where a is first term and d is common difference
For given AP
Kth term = b + (k -1) *(-b/3)
20th value = 15
20th value can be find as:
b + 19 *(-b/3) = 15
so b = -2.81
Sum of first 20 values:
5

Sum = (n/2) * [2a + (n-1)*d]
On substituting values:
Sum = (20/2) * [2*(-2.81) + (20-1)*(-2.8)/3]
= 10 [-5.62 – 19b/3]
= 10/3 [-16.86 + 53.39]
= 10/3 *36.53
= 121.76
Sum of 20 terms = 121.76
(2) Geometric progression
Solution
1, 1/2 , 1/4 ....
a = 1
Formula for nth term = a * r (n-1)
n = 20 and r = 0.5
20th term = 1 * 0.5 (20-1)
20th term = 1/ 524288
(2.) Value of sum
The sum of GP up to infinite number of terms is given by formula: S = a / (1-r)
On substituting values: a = 1 and r = 0.5
Sum = 1 / (1-0.5) = 2
Thus sum is equals to 2
(3) Equations
a.) 2 log 3x + log 18x = 27
Solution
Log 18x = log (3x*6)
2 log 3x + log (3x*6) = 27
2 log 3x + log 3x + log 6 = 27
2 log 3x + log 3x = 26.22
6

3 log x = 26.22
x = 10 (27 – log 162)/3 or 183440402.7
(b) 2 ln 3x + ln 18x = 9
Solution
2 ln 3x + ln 18x = 9
Using the formula: ln (ab) = ln a + ln b
We can write ln 18x = ln3x + ln 6x
2 ln 3x + ln 3x + ln 6 = 9
2 ln 3x + ln 3x = 9 – ln 6
3ln 3x = 9 – ln 6
Using the property: ln xm = m*ln x
So 3ln 3x = ln (3x)3
ln (3x)3 = 9 – ln 6
x = e (9 – ln 162) /3 = 3.68
(c1) coshx + sinhx = 5
Solution
coshx = ex + e-x / 2
sinhx = ex - e-x / 2
[ex + e-x / 2] + [ex - e-x / 2 ] = 5
ex + e-x + ex - e-x = 5*2
2ex = 10
ex = 5
X = ln 5 = 1.60
(c2) cosh2y - sinh2y = 3
Solution
Cosh2y = e2y + e-2y / 2
Sinh2y = e2y - e-2y / 2
[e2y + e-2y / 2] - [e2y - e-2y / 2] = 3
7

e2y + e-2y - e2y + e-2y = 6
2 e-2y = 6
e-2y = 3
-2y = ln 3
Y = -0.5 ln 3
y = -0.5 ln 3 = -0.54
(c3) coshk * sinhk = 2
Solution
coshk = ek + e-k / 2
sinhk = ek - e-k / 2
[ek + e-k / 2] * [ek - e-k / 2] = 2
ek + e-k + ek - e-k = 4
2ek =4
ek = 1
k = 0.5 ln (4 + √17) = 1.19
(c4) coshM / sinhM = 2
Solution
[eM + e-M / 2] / [eM - e-M / 2 ] = 2
X = 0.5 ln 3 = 0.54
TASK 2
Scenario 1
(a) Mode for rectangle distribution and histogram
Solution
Revenu
e
Januar
y July
8

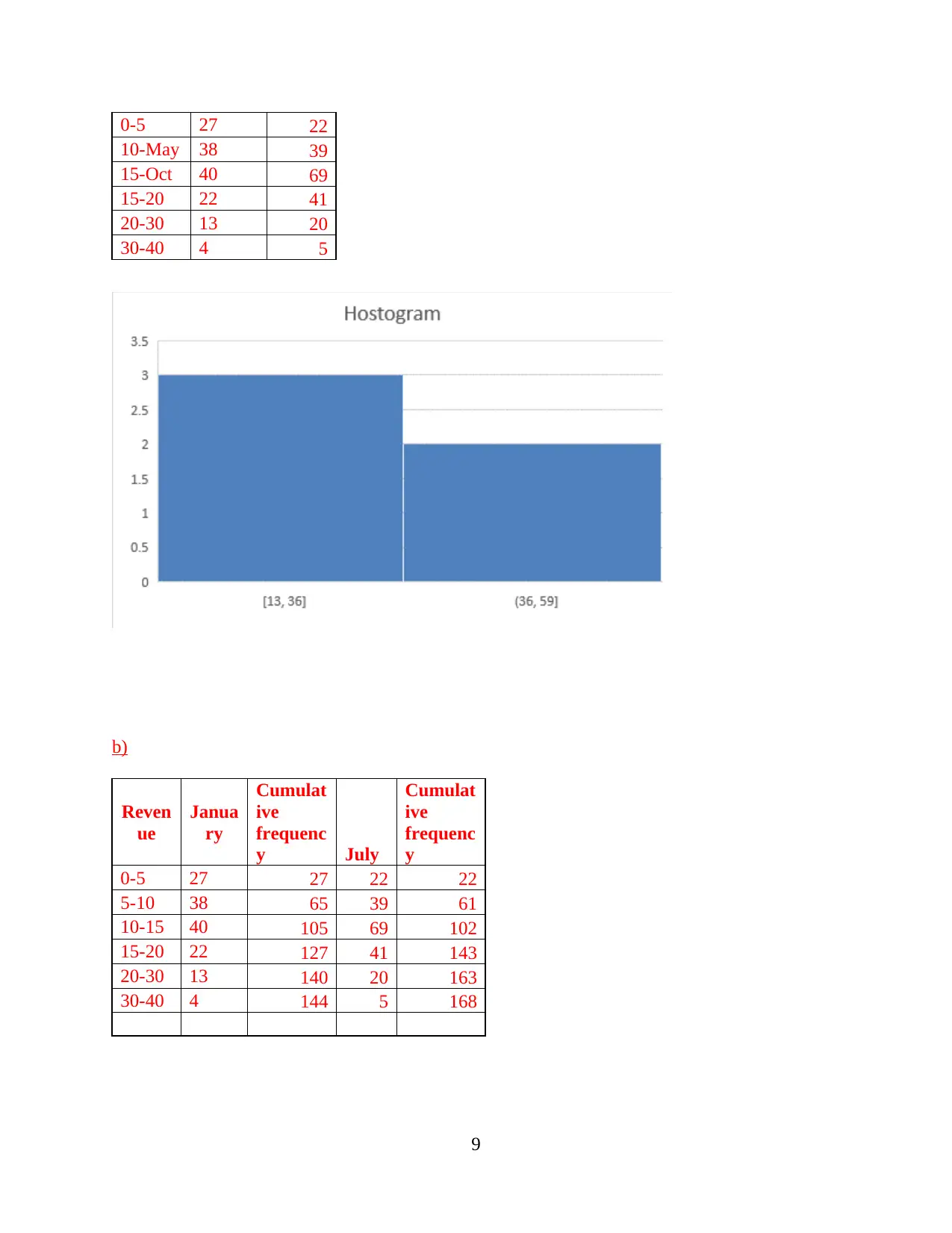
0-5 27 22
10-May 38 39
15-Oct 40 69
15-20 22 41
20-30 13 20
30-40 4 5
b)
Reven
ue
Janua
ry
Cumulat
ive
frequenc
y July
Cumulat
ive
frequenc
y
0-5 27 27 22 22
5-10 38 65 39 61
10-15 40 105 69 102
15-20 22 127 41 143
20-30 13 140 20 163
30-40 4 144 5 168
9

0-5 5-10 10-15 15-20 20-30 30-40
0
20
40
60
80
100
120
140
160
180
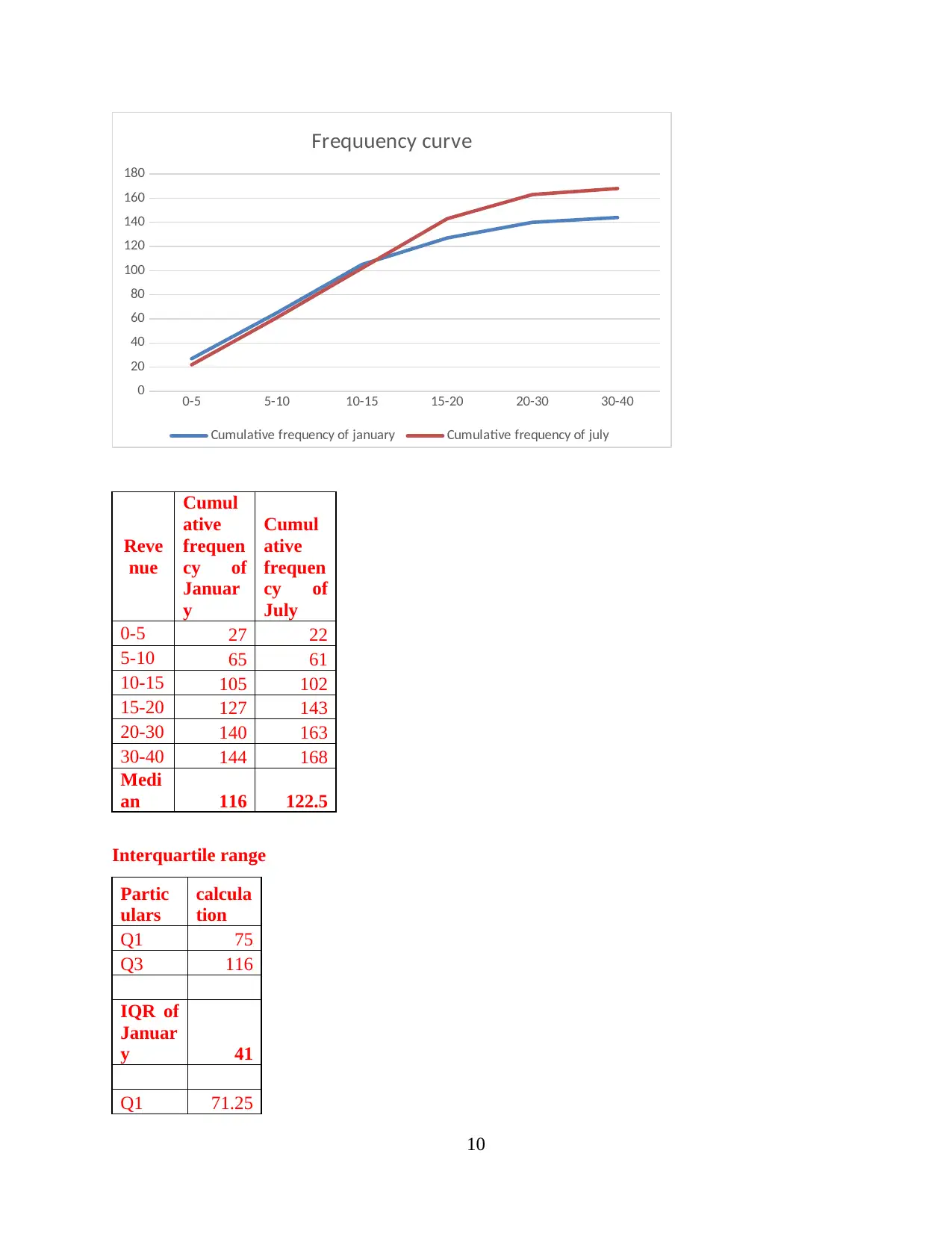
Frequuency curve
Cumulative frequency of january Cumulative frequency of july
Reve
nue
Cumul
ative
frequen
cy of
Januar
y
Cumul
ative
frequen
cy of
July
0-5 27 22
5-10 65 61
10-15 105 102
15-20 127 143
20-30 140 163
30-40 144 168
Medi
an 116 122.5
Interquartile range
Partic
ulars
calcula
tion
Q1 75
Q3 116
IQR of
Januar
y 41
Q1 71.25
10

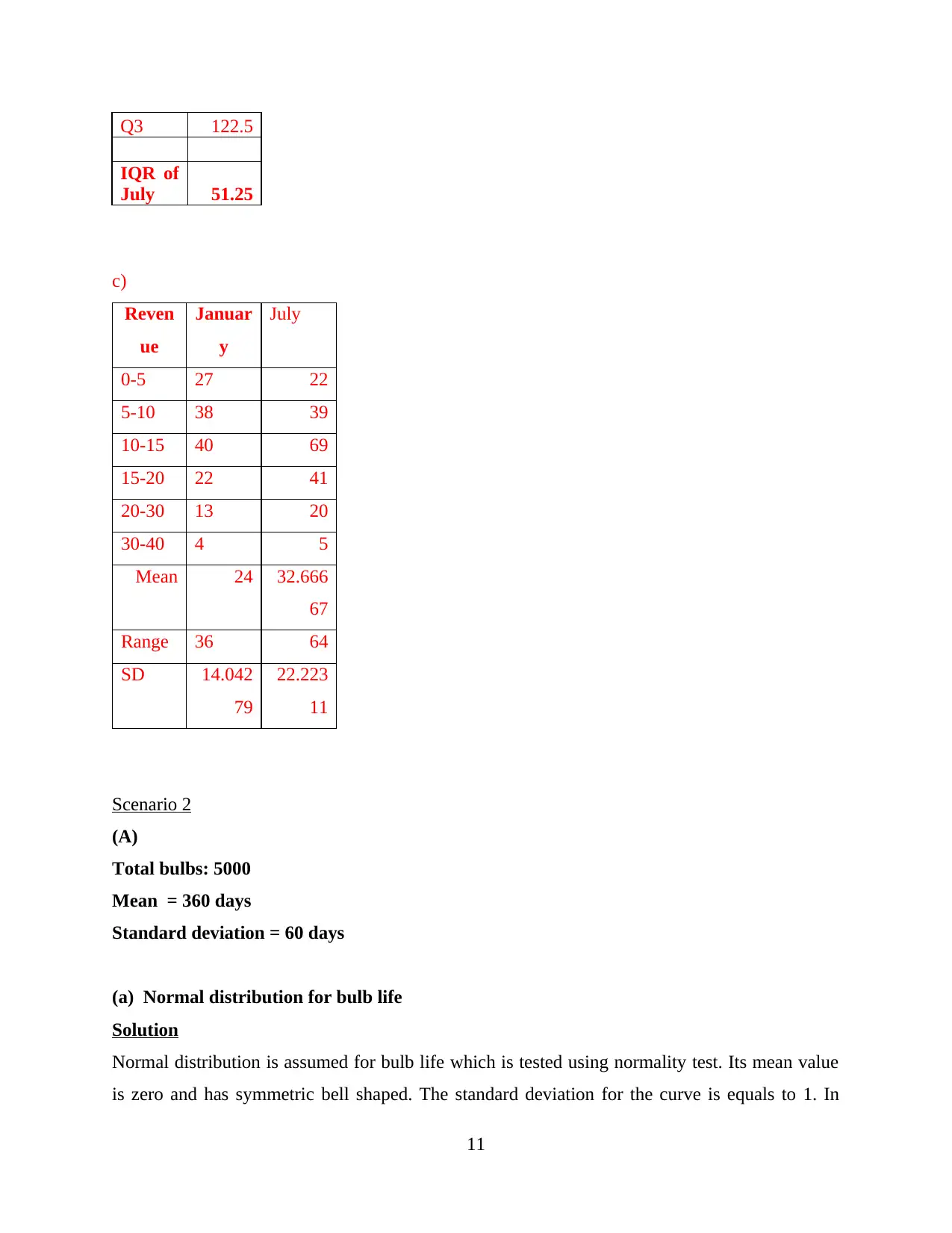
Q3 122.5
IQR of
July 51.25
c)
Reven
ue
Januar
y
July
0-5 27 22
5-10 38 39
10-15 40 69
15-20 22 41
20-30 13 20
30-40 4 5
Mean 24 32.666
67
Range 36 64
SD 14.042
79
22.223
11
Scenario 2
(A)
Total bulbs: 5000
Mean = 360 days
Standard deviation = 60 days
(a) Normal distribution for bulb life
Solution
Normal distribution is assumed for bulb life which is tested using normality test. Its mean value
is zero and has symmetric bell shaped. The standard deviation for the curve is equals to 1. In
11

normal distribution Kurtosis range value is between +7 and -7 while that of skewness range is
given as +2 and -2. On plotting Q-Q plot using both observed and expected value it is seen that
values varying through straight line denotes false assumption and is not representing normal
distribution otherwise it has normal distribution.
(b) Replacement interval
Solution
As given only maximum of 10% bulbs can be permitted to fail prior replacement
Mean and standard deviation values are given as 360 and 60 days respectively.
As per z sore the finalised interval is 0.10. It underlines on -1.28. Hence
Expected time interval of replacement is:
(t-360) / 60 = -1.28 where t represents number of days for replacement
Thus t = 283.2 days
c.) Practical consideration influencing replacement
Solution
12