BUS 270 Test 2 Statistics Solutions - Probability and Distributions

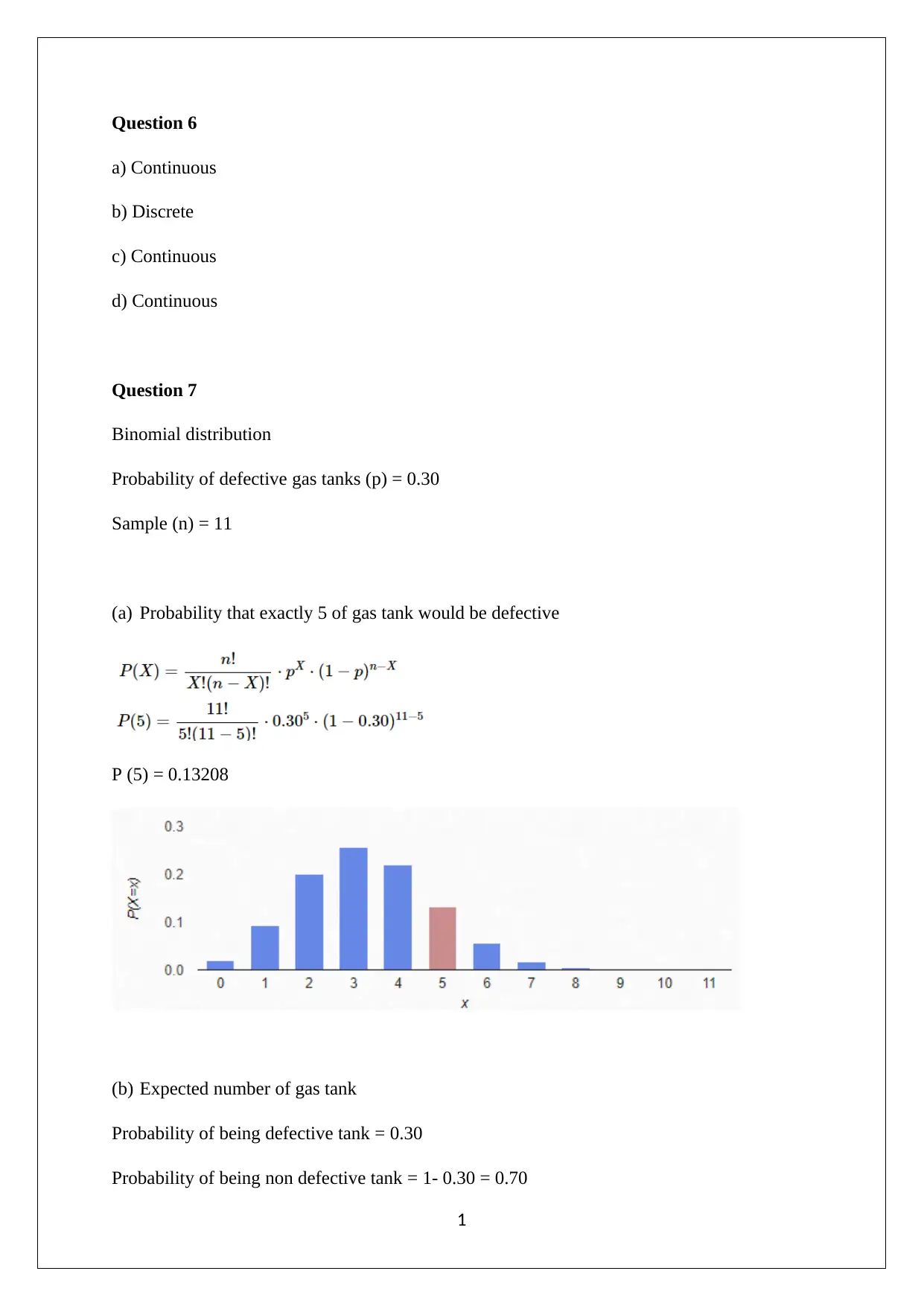
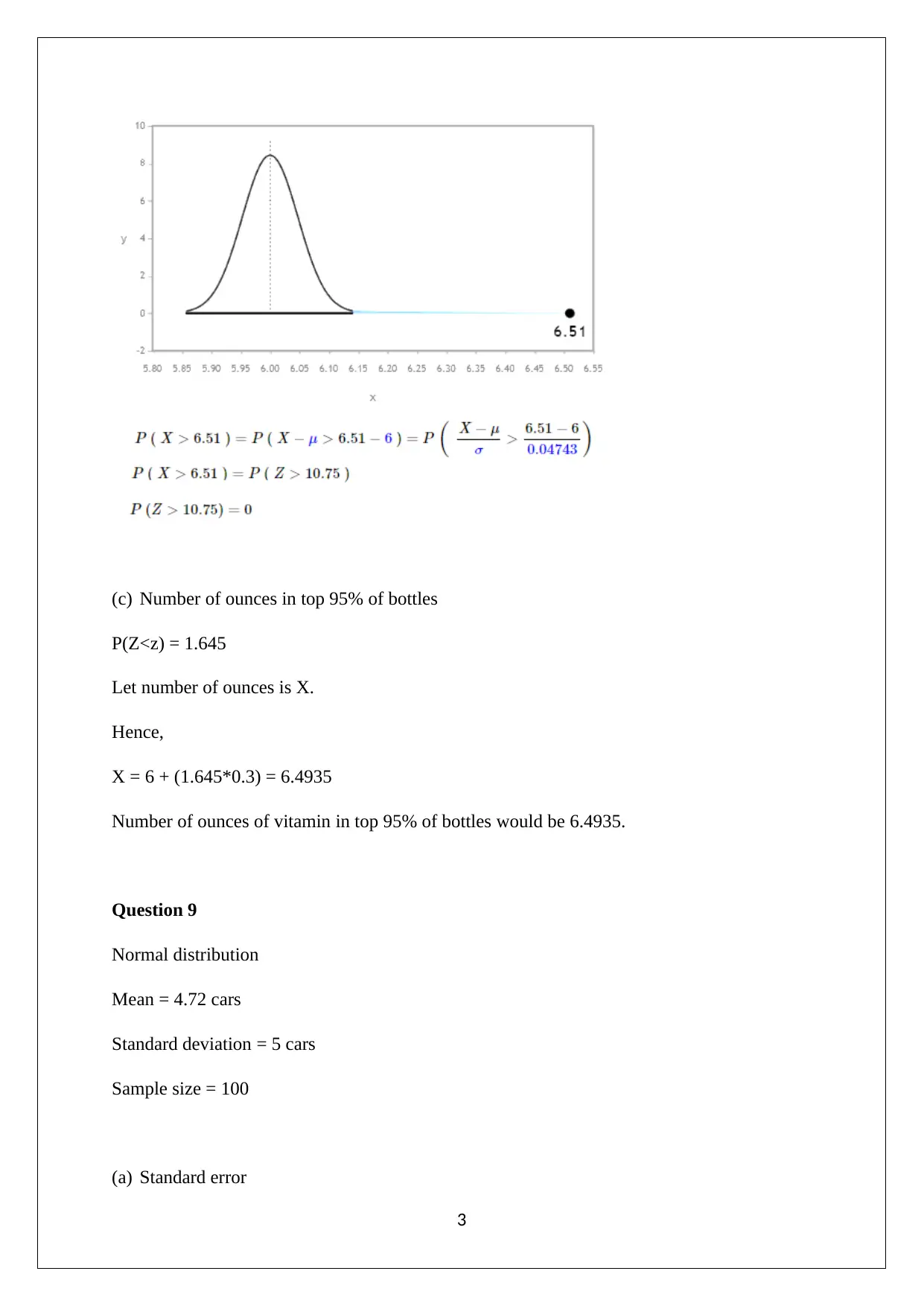
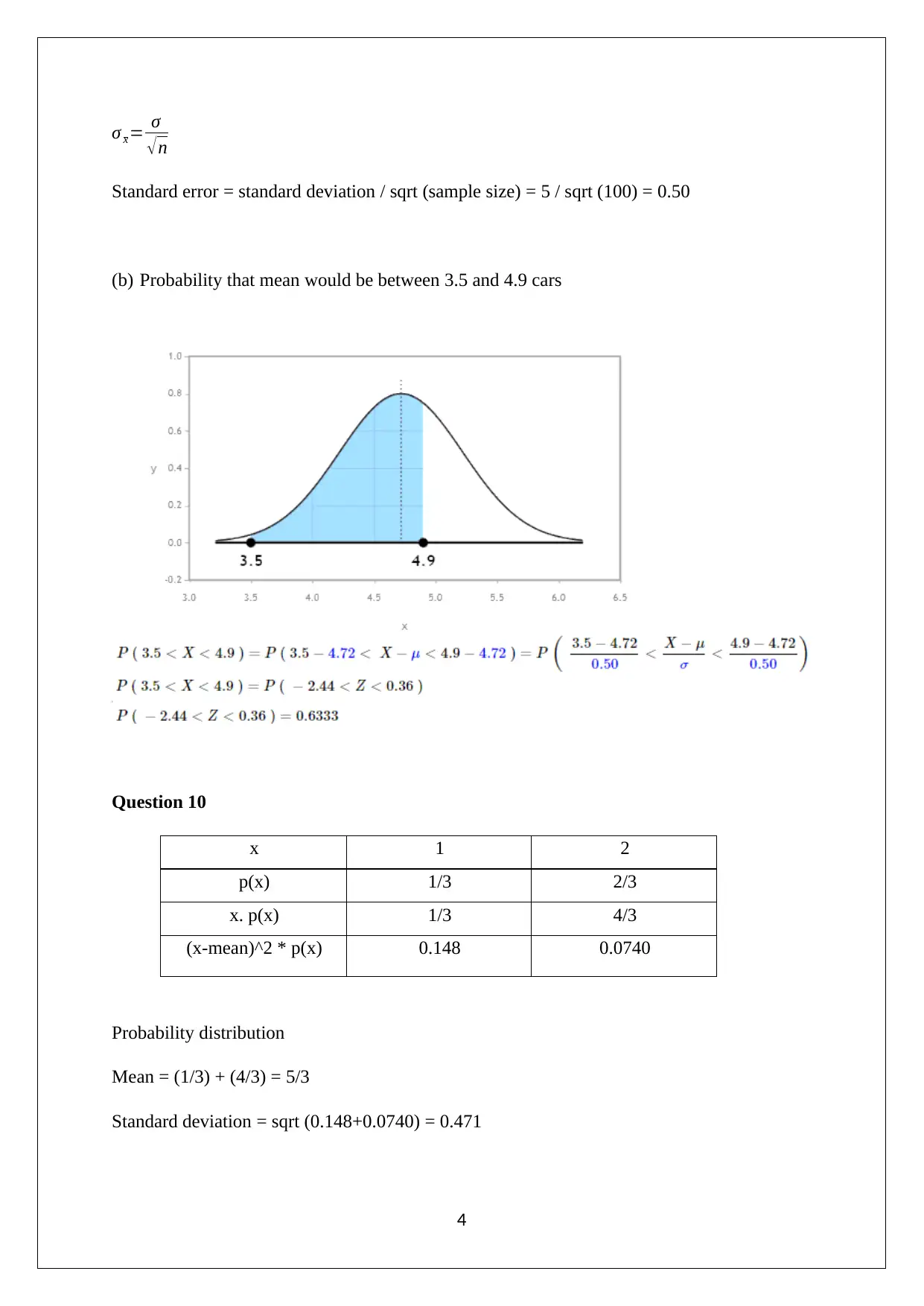
This document contains the solutions to a BUS 270 Statistics Test 2, covering various statistical concepts. The solutions address questions on continuous and discrete variables, binomial distributions, and normal distributions. Calculations include probabilities, expected values, and standard deviations. The document also provides solutions for problems related to the central limit theorem, point estimation, and probability distributions. Specific examples include calculating probabilities for defective gas tanks, determining the percentage of bottles containing a certain amount of vitamin, and finding the probability of a mean value falling within a specific range. The document also includes solutions for extra credit questions related to sample proportions and defective items. Overall, the document provides a comprehensive set of solutions to the test questions, demonstrating a solid understanding of statistical concepts and calculations.

Statistics
[Document subtitle]
[DATE]

Question 6
a) Continuous
b) Discrete
c) Continuous
d) Continuous
Question 7
Binomial distribution
Probability of defective gas tanks (p) = 0.30
Sample (n) = 11
(a) Probability that exactly 5 of gas tank would be defective
P (5) = 0.13208
(b) Expected number of gas tank
Probability of being defective tank = 0.30
Probability of being non defective tank = 1- 0.30 = 0.70
1

Expected number of gas tank = np = 11*0.70 = 77
Question 8
Normal distribution
Mean = 6 ounces
Standard deviation = 0.3 ounces
(a) % of bottles contains greater than 6.51 ounces of vitamin
4.46% of bottles contains greater than 6.51 ounces of vitamin.
(b) Number of bottles of vitamin = 40
Probability that bottle would contain greater than 6.51 ounces of vitamin
σ x= σ
√n
Standard error = standard deviation/ sqrt (sample size) = 0.3 / sqrt (40) = 0.04743
2

(c) Number of ounces in top 95% of bottles
P(Z<z) = 1.645
Let number of ounces is X.
Hence,
X = 6 + (1.645*0.3) = 6.4935
Number of ounces of vitamin in top 95% of bottles would be 6.4935.
Question 9
Normal distribution
Mean = 4.72 cars
Standard deviation = 5 cars
Sample size = 100
(a) Standard error
3

σ x= σ
√n
Standard error = standard deviation / sqrt (sample size) = 5 / sqrt (100) = 0.50
(b) Probability that mean would be between 3.5 and 4.9 cars
Question 10
x 1 2
p(x) 1/3 2/3
x. p(x) 1/3 4/3
(x-mean)^2 * p(x) 0.148 0.0740
Probability distribution
Mean = (1/3) + (4/3) = 5/3
Standard deviation = sqrt (0.148+0.0740) = 0.471
4

Question 11
Distribution
Number sold in a d a y ( x ) 0 1 2 3 4
Probability (Number s o ld ) 0 .0 6 0 .1 8 0 .1 3 0 .1 0 0 .5 3
(a) The probability distribution is valid because the given probabilities are non-negative and
sum of distribution is equal to 1. The two conditions required here is highlighted below.
 The sum of all probabilities of probability distribution must be 1.
 Probabilities must be non-negative.
(b) P(X>=2)
P(X>=2) = 0.13 + 0.10 + 0.53 = 0.76
(c) Number of cheesecakes sells
x p(x) x p(x)
1 0.18 0.18
2 0.13 0.26
3 0.10 0.3
4 0.53 2.12
Total 2.86
Expected value = E(x) = ∑ x . p ( x ) =2.86
Number of cheesecakes sells in a day would be 2.86 or 3.
Question 12 (Extra Credit)
5

Sample = 200
Number of defective items = 10% of 3100 = 3100*10% = 310
(a) Point estimate of proportion of defective item
P = 0.10
(b) Standard error of sample proportion of defective item
Standard erro r = √ p ( 1− p )
n = √0.1 0 1−0.10
2 00 =0.0212
6