BUS105 Computing Assignment: Data Analysis and Interpretation, 2017
VerifiedAdded on 2020/04/01
|15
|2448
|75
Homework Assignment
AI Summary
This document presents a comprehensive solution to a BUS105 computing assignment, encompassing several statistical analysis techniques. The assignment involves analyzing datasets using Excel, focusing on descriptive statistics, hypothesis testing, and confidence intervals. Section 1 analyzes a scatterplot and regression, calculating a z-score and estimating ranks. Section 2 utilizes pivot tables to compare investment types (risky vs. safe) and their profit/loss proportions, including z-score calculations and p-value determination. Section 3 involves further pivot table analysis to compare low and high-risk investments, calculating z-scores and performing hypothesis tests to compare means. Section 4 addresses customer support for a business change, using pivot tables, calculating z-scores, and determining a confidence interval. Section 5 involves creating pivot tables and summarizing the relationship between education level and monthly income. Finally, Section 6 provides a summary of a YouTube video explaining risk and return, including computations of rate of return and risk using provided data. The solution includes graphs, comments on relationships between variables, and interpretations of statistical results.

Title: bus105 computing assignment semester 2, 2017
Name:
Student number:
Allocated sample: 116
Name:
Student number:
Allocated sample: 116
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Section 1
Use the dataset given below you must use the sample allocated to you based on your student
number
https://app.box.com/s/56pb6hqu0ypcg0f3lhy6cl5szt1jgdla
Note that for section 1 the answers are provided so you can check your work, the answers
will not be provided for the other sections.
A) paste in the scatterplot for your sample into your word document and give a simple
comment about the relationship between the variables, (you do not need to submit the
excel file)
Solution
B) Estimate the annual contribution if the income is $200,000 using the regression line
from part (a)
Solution
Regression equation is;
y=0.1379 x−1668.2
With an income of $200,000 we have annual contribution s;
y=0.1379∗( 200000 ) −1668.2
y=$ 25911.8
Thus the estimated annual contribution is $25911.8
C) Find the z-score of the estimate in part (B) note that average of the estimates is
$27,000 with standard deviation $2,100, remember to show your work.
Solution
2
Use the dataset given below you must use the sample allocated to you based on your student
number
https://app.box.com/s/56pb6hqu0ypcg0f3lhy6cl5szt1jgdla
Note that for section 1 the answers are provided so you can check your work, the answers
will not be provided for the other sections.
A) paste in the scatterplot for your sample into your word document and give a simple
comment about the relationship between the variables, (you do not need to submit the
excel file)
Solution
B) Estimate the annual contribution if the income is $200,000 using the regression line
from part (a)
Solution
Regression equation is;
y=0.1379 x−1668.2
With an income of $200,000 we have annual contribution s;
y=0.1379∗( 200000 ) −1668.2
y=$ 25911.8
Thus the estimated annual contribution is $25911.8
C) Find the z-score of the estimate in part (B) note that average of the estimates is
$27,000 with standard deviation $2,100, remember to show your work.
Solution
2

Z= x −μ
σ =25911.8−27000
2100 =−0.51819
D) using the z-score from part (C) Find P(Z<z-score) , you can find out the answer using
www.wolframalpha.com
for example found the z-score was 1.5 if the z-score is 1.5 type in
P(Z<1.5)
into wolfram alpha.com
Solution
P ( Z <z−score ) =P ( Z <−0.51819 ) =0.3022
E) If there was a list of 10,000 estimates ranked from lowest to highest, what rank do you
think your estimate would be close to?
Hint: just use the formula
expected rank = P(Z<z-score)*10000, remember to show your work.
Solution
Expected rank =P ( Z < z−score )∗10000=0.3022∗10000=3022
Section 2
Use the dataset given below you must use the sample allocated to you based on your student
number
https://app.box.com/s/yvhk3e3oymbs3toy6j5xetid82dsjyz4
A) Use the PivotTable feature in excel to find appropriate summary statistics for your
sample, This will probably require two PivotTables. You should paste both into word,
you do not need the excel file.
Make sure the pivotable (or pivottables) include the following statistics
*Just considering the high risk (riskier type) investments what is the sample size n1
and the proportion of high risk investments that made a loss ^p1
*Just considering the low risk (safer type) investments what is the sample size =n2 and
What is the proportion of low risk investments that made a loss ^p2
Solution
3
σ =25911.8−27000
2100 =−0.51819
D) using the z-score from part (C) Find P(Z<z-score) , you can find out the answer using
www.wolframalpha.com
for example found the z-score was 1.5 if the z-score is 1.5 type in
P(Z<1.5)
into wolfram alpha.com
Solution
P ( Z <z−score ) =P ( Z <−0.51819 ) =0.3022
E) If there was a list of 10,000 estimates ranked from lowest to highest, what rank do you
think your estimate would be close to?
Hint: just use the formula
expected rank = P(Z<z-score)*10000, remember to show your work.
Solution
Expected rank =P ( Z < z−score )∗10000=0.3022∗10000=3022
Section 2
Use the dataset given below you must use the sample allocated to you based on your student
number
https://app.box.com/s/yvhk3e3oymbs3toy6j5xetid82dsjyz4
A) Use the PivotTable feature in excel to find appropriate summary statistics for your
sample, This will probably require two PivotTables. You should paste both into word,
you do not need the excel file.
Make sure the pivotable (or pivottables) include the following statistics
*Just considering the high risk (riskier type) investments what is the sample size n1
and the proportion of high risk investments that made a loss ^p1
*Just considering the low risk (safer type) investments what is the sample size =n2 and
What is the proportion of low risk investments that made a loss ^p2
Solution
3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
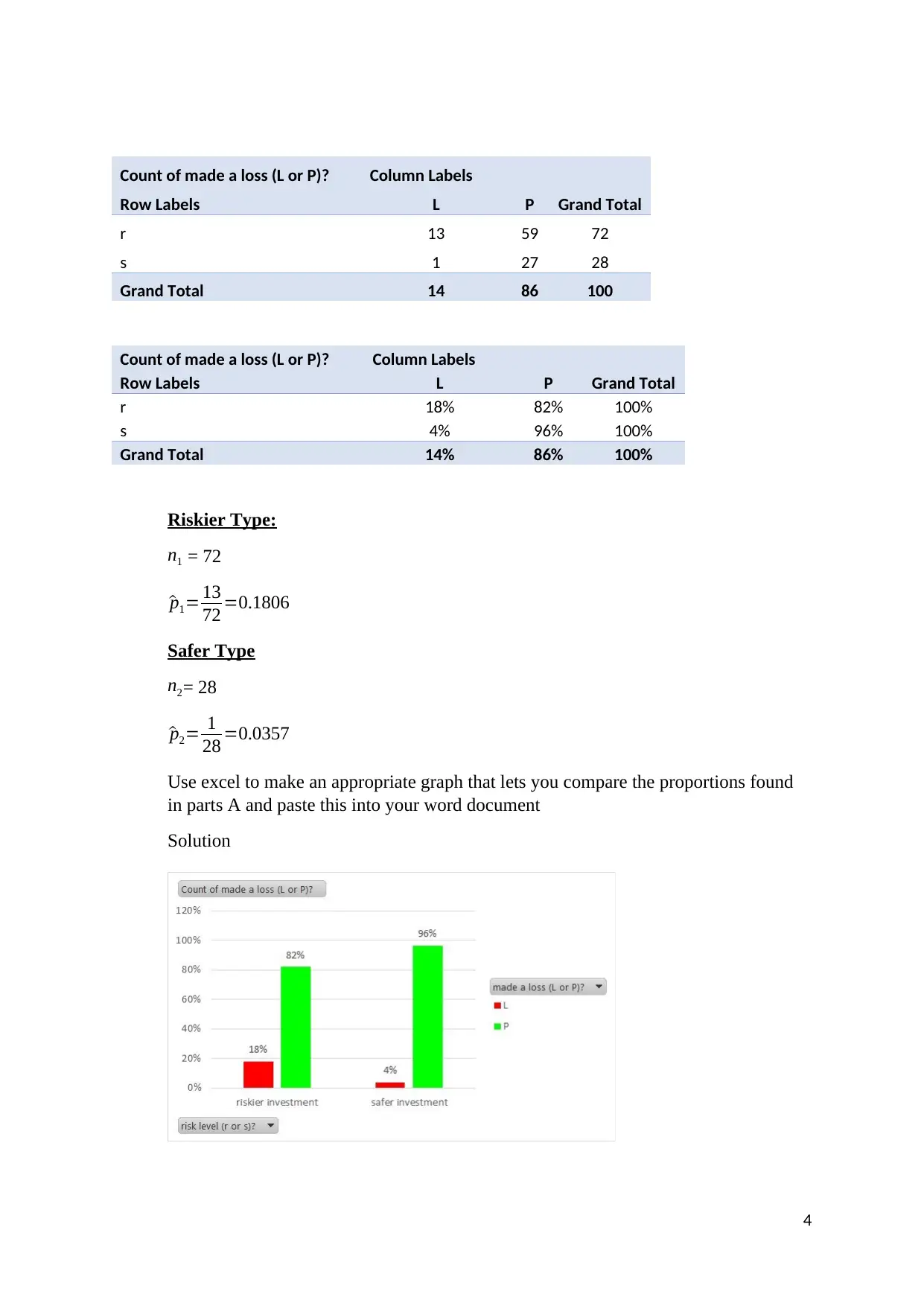
Count of made a loss (L or P)? Column Labels
Row Labels L P Grand Total
r 13 59 72
s 1 27 28
Grand Total 14 86 100
Count of made a loss (L or P)? Column Labels
Row Labels L P Grand Total
r 18% 82% 100%
s 4% 96% 100%
Grand Total 14% 86% 100%
Riskier Type:
n1 = 72
^p1= 13
72 =0.1806
Safer Type
n2= 28
^p2= 1
28 =0.0357
Use excel to make an appropriate graph that lets you compare the proportions found
in parts A and paste this into your word document
Solution
4
Row Labels L P Grand Total
r 13 59 72
s 1 27 28
Grand Total 14 86 100
Count of made a loss (L or P)? Column Labels
Row Labels L P Grand Total
r 18% 82% 100%
s 4% 96% 100%
Grand Total 14% 86% 100%
Riskier Type:
n1 = 72
^p1= 13
72 =0.1806
Safer Type
n2= 28
^p2= 1
28 =0.0357
Use excel to make an appropriate graph that lets you compare the proportions found
in parts A and paste this into your word document
Solution
4
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

B) Looking at your answers to parts (A) and (B) Make a simple comment about the
relationship between the variables
investment type (risky or safe ) and
Made a profit (made a profit/made a loss)
Solution
Large proportion (96%) of safer investments recorded profits as compared to the
riskier investments (82% made profits).
i) Using your sample what is the estimate for p1- p2? In other words what is the
difference between the sample proportions ^p1 - ^p2
Solution
^p1− ^p2=0.1806−0.0357=0. 1449
ii) Find the z-score of the estimate in part (i) note that average of the estimates is
0.1 with standard deviation 0.0743
Solution
z= 0.1449−0.1
0.0743 =0.6043
iii) Using part (ii) find P(Z<z-score) using www.wolframalpha.com
for example if the z-score is 0.5 type in
P(Z<0.5)”
into wolframalpha.com
Solution
P ( Z < z−score ) =P ( Z <0.06043 )=0.7272
iv) IF there was a list of 4000 estimates ranked from lowest to highest, roughly
what rank do you expect your estimate to have?
Hint: just use the formula
expected rank = P(Z<z-score)*4000
5
relationship between the variables
investment type (risky or safe ) and
Made a profit (made a profit/made a loss)
Solution
Large proportion (96%) of safer investments recorded profits as compared to the
riskier investments (82% made profits).
i) Using your sample what is the estimate for p1- p2? In other words what is the
difference between the sample proportions ^p1 - ^p2
Solution
^p1− ^p2=0.1806−0.0357=0. 1449
ii) Find the z-score of the estimate in part (i) note that average of the estimates is
0.1 with standard deviation 0.0743
Solution
z= 0.1449−0.1
0.0743 =0.6043
iii) Using part (ii) find P(Z<z-score) using www.wolframalpha.com
for example if the z-score is 0.5 type in
P(Z<0.5)”
into wolframalpha.com
Solution
P ( Z < z−score ) =P ( Z <0.06043 )=0.7272
iv) IF there was a list of 4000 estimates ranked from lowest to highest, roughly
what rank do you expect your estimate to have?
Hint: just use the formula
expected rank = P(Z<z-score)*4000
5

Solution
Expected rank =P ( Z < z−score )∗10000=0.7272∗4000=2909
C) Test the claim there is a difference in the proportions use a 5% level of significance
i) State an appropriate H0 and H1
Solution
ii) Find the p-value Only using the answers to part (A) and the webpage
http://epitools.ausvet.com.au/content.php?page=z-test-2
Do NOT use any other method to find the p-value
Do NOT use any other software package such as SPSS or Analysis tookpak
Solution
Sample 1 Sample 2 Difference
Sample proportion 0.1806 0.0357 0.1449
95% CI (asymptotic) 0.0917 - 0.2695 -0.033 - 0.1044 -0.0066 - 0.2964
z-value 1.9
P-value 0.0608
Interpretation
Not significant,
accept null hypothesis that
sample proportions are equal
n by pi n * pi <=5, test inappropriate
iii) State whether or not you reject the H0
Solution
Since p-value is greater than α = 0.05. we fail to reject the null hypothesis
iv) Give a conclusion in plain English
Solution
6
Expected rank =P ( Z < z−score )∗10000=0.7272∗4000=2909
C) Test the claim there is a difference in the proportions use a 5% level of significance
i) State an appropriate H0 and H1
Solution
ii) Find the p-value Only using the answers to part (A) and the webpage
http://epitools.ausvet.com.au/content.php?page=z-test-2
Do NOT use any other method to find the p-value
Do NOT use any other software package such as SPSS or Analysis tookpak
Solution
Sample 1 Sample 2 Difference
Sample proportion 0.1806 0.0357 0.1449
95% CI (asymptotic) 0.0917 - 0.2695 -0.033 - 0.1044 -0.0066 - 0.2964
z-value 1.9
P-value 0.0608
Interpretation
Not significant,
accept null hypothesis that
sample proportions are equal
n by pi n * pi <=5, test inappropriate
iii) State whether or not you reject the H0
Solution
Since p-value is greater than α = 0.05. we fail to reject the null hypothesis
iv) Give a conclusion in plain English
Solution
6
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
We conclude that there is no significant evidence to show that the proportion
of loss for the two types of investments (safer and riskier investments) is
different at 5% level of significance.
Section 3
Use the dataset given below you must use your own sample
https://app.box.com/s/z0mbtcfsdqxz1rm7rhw3p9sb75aq7174
A) Use the pivot table feature in excel to find appropriate summary statistics for your
sample. The following sample statistics must be found
Just considering the low risk investments, what is the sample size n1 , the sample
average return of low risk investments x1 , and the sample standard deviation s1
Just considering the high risk investments , what is the sample size n2 , the sample
average return of high risk investments x2 , and the sample standard deviation s2
Paste the pivot table into the word document you do not need to submit the excel file
Solution
Row Labels
Average of
return
StdDev of
return
Count of High
risk?
Low risk investment 0.03542 0.00311 69
High risk investment 0.07613 0.08570 31
Grand Total 0.04804 0.05090 100
Low risk investments
n1 = 69
x1 = 0.03542
s1 = 0.00311
7
of loss for the two types of investments (safer and riskier investments) is
different at 5% level of significance.
Section 3
Use the dataset given below you must use your own sample
https://app.box.com/s/z0mbtcfsdqxz1rm7rhw3p9sb75aq7174
A) Use the pivot table feature in excel to find appropriate summary statistics for your
sample. The following sample statistics must be found
Just considering the low risk investments, what is the sample size n1 , the sample
average return of low risk investments x1 , and the sample standard deviation s1
Just considering the high risk investments , what is the sample size n2 , the sample
average return of high risk investments x2 , and the sample standard deviation s2
Paste the pivot table into the word document you do not need to submit the excel file
Solution
Row Labels
Average of
return
StdDev of
return
Count of High
risk?
Low risk investment 0.03542 0.00311 69
High risk investment 0.07613 0.08570 31
Grand Total 0.04804 0.05090 100
Low risk investments
n1 = 69
x1 = 0.03542
s1 = 0.00311
7
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

High risk investments
n2 = 31
x2 = 0.07613
s2 = 0.08570
B) Give an appropriate graph that shows the relationship between variables, Note that the
information in part A is NOT Suitable for a graph you have to get different
information
Solution
C) Make a simple comment about the relationship between the variables using the
answers to (A) and (B)
The highest proportion of investments (69%) is the high risk investment, low
investment was represented by 31%. However, the low risk investment had the lowest
average returns (0.03542) compared to the high risk investment (0.07613).
D)
i) Using your sample what is the estimate for μ1- μ2? In other words what is the
difference between the sample means x1- x2
8
n2 = 31
x2 = 0.07613
s2 = 0.08570
B) Give an appropriate graph that shows the relationship between variables, Note that the
information in part A is NOT Suitable for a graph you have to get different
information
Solution
C) Make a simple comment about the relationship between the variables using the
answers to (A) and (B)
The highest proportion of investments (69%) is the high risk investment, low
investment was represented by 31%. However, the low risk investment had the lowest
average returns (0.03542) compared to the high risk investment (0.07613).
D)
i) Using your sample what is the estimate for μ1- μ2? In other words what is the
difference between the sample means x1- x2
8

Solution
x1−x2
0.03542 - 0.07613 = -0.04071
ii) Find the z-score of the estimate in part (i) note that average of the estimates -
0.0256 with standard deviation 0.0173
Solution
z=−0.04071
0.0173 =−2.35317
iii) Using part (ii) What is P(Z<z-score), you can find out the answer using
www.wolframalpha.com
for example if the z-score =-1 type in
P(Z<-1)
into wolfram alpha
Solution
P(Z<z-score) = P(Z< -2.353179) = 0.0093
iv) If there was a list of 2000 estimates ranked from lowest to highest, what rank
do you think your would be close to, hint just use the formula
expected rank = P(Z<z-score)*2000
Solution
Expected rank = P(Z<z-score)*2000
Expected rank = 0.0093*2000 = 19
E) Test the claim that there is a difference between the means using a 5% level of
significance
i) State an appropriate H0 and H1
Solution
9
x1−x2
0.03542 - 0.07613 = -0.04071
ii) Find the z-score of the estimate in part (i) note that average of the estimates -
0.0256 with standard deviation 0.0173
Solution
z=−0.04071
0.0173 =−2.35317
iii) Using part (ii) What is P(Z<z-score), you can find out the answer using
www.wolframalpha.com
for example if the z-score =-1 type in
P(Z<-1)
into wolfram alpha
Solution
P(Z<z-score) = P(Z< -2.353179) = 0.0093
iv) If there was a list of 2000 estimates ranked from lowest to highest, what rank
do you think your would be close to, hint just use the formula
expected rank = P(Z<z-score)*2000
Solution
Expected rank = P(Z<z-score)*2000
Expected rank = 0.0093*2000 = 19
E) Test the claim that there is a difference between the means using a 5% level of
significance
i) State an appropriate H0 and H1
Solution
9
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

H0 : μ1−μ2=0
H1 : μ1−μ2 ≠ 0
ii) Find the p-value using the answers to part (A))and the webpage
https://www.medcalc.org/calc/comparison_of_means.php
Do NOT find the p-value using any other method.
Do NOT use any other software package such as SPSS or Analysis tookpak
Solution
Difference 0.041
Standard error 0.010
95% CI 0.0203 to 0.0611
t-statistic 3.965
DF 98
Significance level P = 0.0001
iii) State whether or not you reject H0
Solution
Since the p-value is less than α = 0.05, we reject the null hypothesis
iv) Give a conclusion in plain English
Solution
We can conclude that there is significant evidence that the mean returns for
the two investments are different. Specifically, the mean returns for the high
risk investment is higher than that of the low risk investment.
10
H1 : μ1−μ2 ≠ 0
ii) Find the p-value using the answers to part (A))and the webpage
https://www.medcalc.org/calc/comparison_of_means.php
Do NOT find the p-value using any other method.
Do NOT use any other software package such as SPSS or Analysis tookpak
Solution
Difference 0.041
Standard error 0.010
95% CI 0.0203 to 0.0611
t-statistic 3.965
DF 98
Significance level P = 0.0001
iii) State whether or not you reject H0
Solution
Since the p-value is less than α = 0.05, we reject the null hypothesis
iv) Give a conclusion in plain English
Solution
We can conclude that there is significant evidence that the mean returns for
the two investments are different. Specifically, the mean returns for the high
risk investment is higher than that of the low risk investment.
10
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Section 4
Use the dataset given below you must use your own sample
https://app.box.com/s/kzc6ivy10gvy4vz6d0pgy0lzh929ivx9
Suppose A business has conducted an opinion poll to find out if their customers support a
change to the Business
a) Use the PivotTable feature in excel to find appropriate summary statistics for your
sample,. You should paste both into word, you do not need the excel file.
This pivot table must have the number of people that answer yes and the number of
people that answer no
Solution
Row Labels Count of do you support proposed change?
no 91
yes 102
Grand Total 193
b) What is sample size and the sample proportion ^p of people that support the change,
Note that ^p is the estimate for the population proportion p
Solution
^p= 102
193 =0.5285
c)
i) Find the z-score of the estimate in part (a) note that average of the estimates
0.6 is with standard deviation 0.0357
Solution
z= 0.5285−0.6
0.0357 =−2.0028
11
Use the dataset given below you must use your own sample
https://app.box.com/s/kzc6ivy10gvy4vz6d0pgy0lzh929ivx9
Suppose A business has conducted an opinion poll to find out if their customers support a
change to the Business
a) Use the PivotTable feature in excel to find appropriate summary statistics for your
sample,. You should paste both into word, you do not need the excel file.
This pivot table must have the number of people that answer yes and the number of
people that answer no
Solution
Row Labels Count of do you support proposed change?
no 91
yes 102
Grand Total 193
b) What is sample size and the sample proportion ^p of people that support the change,
Note that ^p is the estimate for the population proportion p
Solution
^p= 102
193 =0.5285
c)
i) Find the z-score of the estimate in part (a) note that average of the estimates
0.6 is with standard deviation 0.0357
Solution
z= 0.5285−0.6
0.0357 =−2.0028
11

ii) Using part (i) what is P(Z<z-score) you can find out the answer using
www.wolframalpha.com
For example if the z-score is 2 then enter
P(Z<2)
into www.wolframalpha.com
Solution
P(Z< z−score)=P( Z←2.0028)=0.0226
iii) If there was a list of 1000 estimates ranked from lowest to highest, what rank
do you think your would be close to, hint just use the formula
expected rank = P(Z<z-score)*1000
Solution
Expected rank = P(Z<z-score)*1000
Expected rank = 0.0226*1000 = 3
d) Find a 95% confidence interval for the proportion of people that support the change
Solution
Confidence Interval is given as;
P ± Zα / 2 Sp
Sp= √ P(1−P)
n = √ 0.5285 (1−0.5285)
193 =0.035932
P ± Zα / 2 Sp
0.5285 ± 1.96 ( 0.035932 )
0.5285 ± 0.070427
Lower bound: 0.4581
Upper bound: 0.5989
Thus the C.I: [0.4581, 0.5989]
Section 5
12
www.wolframalpha.com
For example if the z-score is 2 then enter
P(Z<2)
into www.wolframalpha.com
Solution
P(Z< z−score)=P( Z←2.0028)=0.0226
iii) If there was a list of 1000 estimates ranked from lowest to highest, what rank
do you think your would be close to, hint just use the formula
expected rank = P(Z<z-score)*1000
Solution
Expected rank = P(Z<z-score)*1000
Expected rank = 0.0226*1000 = 3
d) Find a 95% confidence interval for the proportion of people that support the change
Solution
Confidence Interval is given as;
P ± Zα / 2 Sp
Sp= √ P(1−P)
n = √ 0.5285 (1−0.5285)
193 =0.035932
P ± Zα / 2 Sp
0.5285 ± 1.96 ( 0.035932 )
0.5285 ± 0.070427
Lower bound: 0.4581
Upper bound: 0.5989
Thus the C.I: [0.4581, 0.5989]
Section 5
12
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 15
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





