Bus105 Computing Assignment: Statistical Analysis in Finance

The Bus 105 computing assignment from the second semester of 2017 focuses on applying statistical methods in finance. Section 1 covers regression analysis where predictions are made based on income levels. Z-scores and p-values are computed for probability assessments. In Section 2, hypothesis testing is used to compare sample proportions with population parameters, employing confidence intervals. Section 3 awaits instructor-provided data samples. Finally, Section 6 discusses the importance of mean and standard deviation in finance, emphasizing their role in risk and return analysis. Statistical tools provide a snapshot view essential for financial planning and investment decisions.

Title : Bus105 computing assignment semester 2, 2017
Name:
Student number
Allocated sample: 56

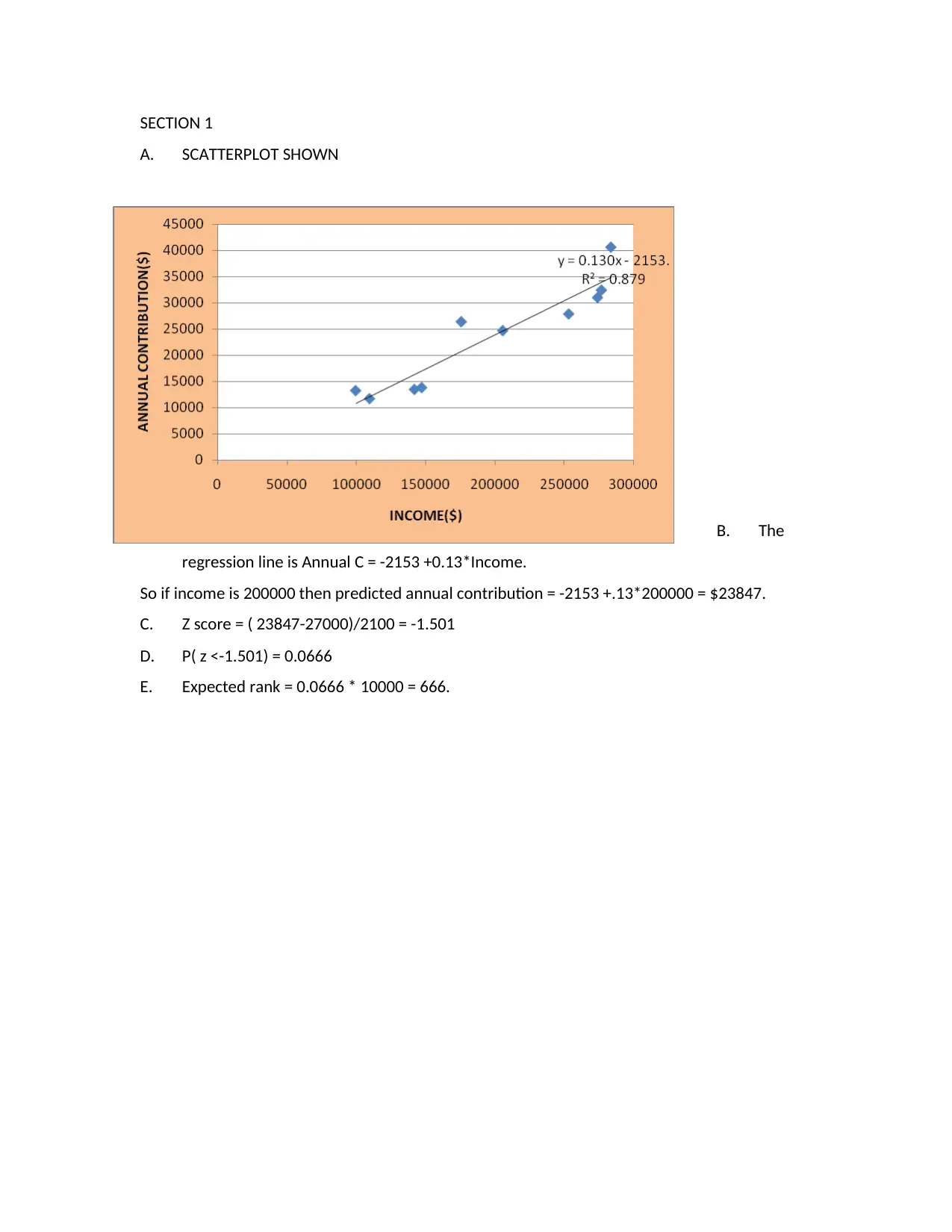
SECTION 1
A. SCATTERPLOT SHOWN
B. The
regression line is Annual C = -2153 +0.13*Income.
So if income is 200000 then predicted annual contribution = -2153 +.13*200000 = $23847.
C. Z score = ( 23847-27000)/2100 = -1.501
D. P( z <-1.501) = 0.0666
E. Expected rank = 0.0666 * 10000 = 666.

Section 2
A. p1 = 0.176 , n1 = 68; n2 = 32 and p2 = 0.125.
B. the graph is below for sample size and risk separately:
C. The probability of a making a loss on risky investment is 0.176. the probability of making a loss
on safe investments is lower at 0.125.
D. i. Using the values p1-p2 = 0.0514
ii. Z score = ( 0.0514 -0.1)/0.0743 = -0.653
iii. P(z < -0.653) = 0.2568
iv. Expected rank = 4000 *.2568 = 1027.3 or 1028 after rounding off.
E. i. Ho: p1-p2 = 0
H1: p1 - p2 ≠ 0
ii. p value = 2*P( z < -.653) = 0.513 ( we multiply with 2 as this is a 2 tail test)
iii. as the level of significance is 0.05 we compare p value with 0.05. p value > 0.05 so we DO NOT
REJECT the null hypothesis.

iv. We can say that there is no difference in the chances of making a loss, across safe and risky
investments.

Section 3
A. Pivot table is shown below
Average of
return
Count of
retu
rn
StdDev of
retur
n
low risk 0.0345 65 0.0032
HighRisk 0.0591 35 0.0942
the sample size n1 = 65
sample average return of low risk investments = 0.0345
sample standard deviation s1 = 0.0032
the sample size n2 = 35
sample average return of high risk investments = 0.0591
sample standard deviation s2 = 0.0942
B.

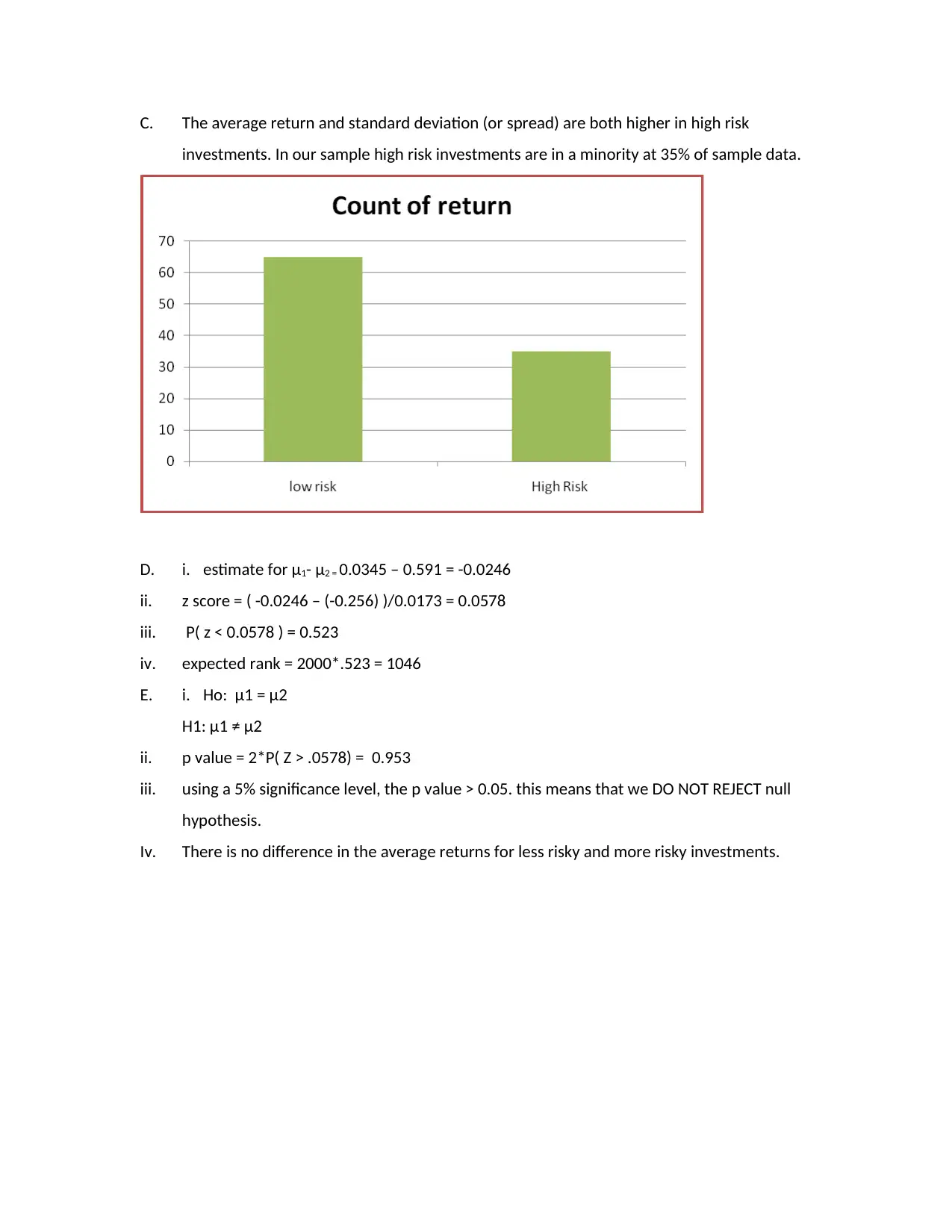
C. The average return and standard deviation (or spread) are both higher in high risk
investments. In our sample high risk investments are in a minority at 35% of sample data.
D. i. estimate for μ1- μ2 = 0.0345 – 0.591 = -0.0246
ii. z score = ( -0.0246 – (-0.256) )/0.0173 = 0.0578
iii. P( z < 0.0578 ) = 0.523
iv. expected rank = 2000*.523 = 1046
E. i. Ho: μ1 = μ2
H1: μ1 ≠ μ2
ii. p value = 2*P( Z > .0578) = 0.953
iii. using a 5% significance level, the p value > 0.05. this means that we DO NOT REJECT null
hypothesis.
Iv. There is no difference in the average returns for less risky and more risky investments.

Section 4
a.
Values
Yes no
119 102
b. n1 = 221 and p = 119/221 = 0.538
c. i. z score = (0.538 -0.6)/0.0357 = -1.737
ii. P ( z < -1.737) = 0.041.
iv. expected rank = 1000*0.041 = 41
d. the confidence interval is proportion estimate ± 1.96*( SE)
where SE = standard error = (0.538*(1-0.538)/221)^.5 = 0.0335
the interval is 0.538 ± 1.96*0.0335 = (0.4722 , 0.6037)

SECTION 5
Waiting for your instructor’s data sample
Section 6
The use of mean and standard deviation is commonplace in subjects as varied as psychology
and economics. Their use in finance is particularly important as finance deals with
numbers. The use of these numbers is the base of any finance related issue or topic.
Mean is a convenient tool that summarizes a dataset easily, ad it is open to
mathematical complexities and arrangements. Though it is affected by extreme values
it is a good measure of central tendency when such extremities are absent. Its ease of
calculation and ability to handle all kinds of variables adds t its benefits. In the same
way, standard deviation is a simple tool to measure the spread of data.
In areas of risk and reward, which form the core of finance the use of mean and standard
deviation is common and well established. These two provide a good and quick
snapshot of the data. The average returns on any asset, for example gives a good view
of what to expect in terms of returns over time. The unevenness of these returns is
captured by standard deviation.
In other areas like rates and returns on assets, the men can be good way to iron out the
highs and lows, and present a balanced kind of view on what returns can be expected
from any asset. This becomes critical when investments are being planned.
The use of mean and standard deviation (or variance) is so common that it is often the first
characteristic that everyone looks at, and are routinely used in articles, news reports
etc. This proves their usefulness to a non statistical person as well.

REFERENCES
Kean.edu, n.d. Confidence Inteval for Mean. [Online] Available at:
http://www.kean.edu/~fosborne/bstat/06amean.html [Accessed 16 Sep 2017].
Learn,bu.edu, n.d. The 5 steps in Hypothesis testing. [Online] Available at:
https://learn.bu.edu/bbcswebdav/pid-826908-dt-content-rid-2073693_1/courses/
13sprgmetcj702_ol/week04/metcj702_W04S01T05_fivesteps.html [Accessed 15 Sep 2017].
stat.ualberta.ca, n.d. What isa P value. [Online] Available
athttp://www.stat.ualberta.ca/~hooper/teaching/misc/Pvalue.pdf [Accessed 19 Sep 2017].