Business Analytics Project: CAT Inc. Optimization Solution

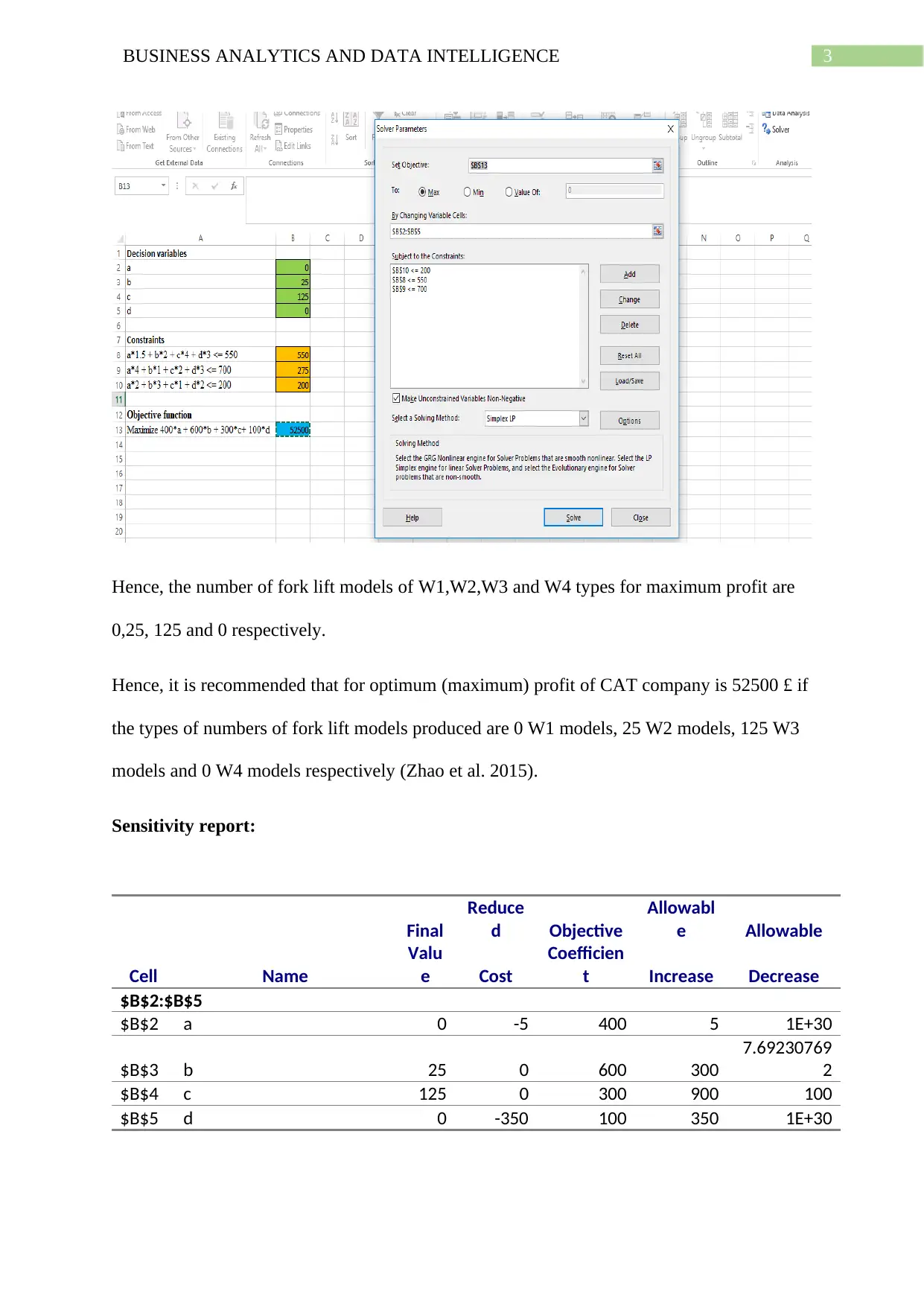
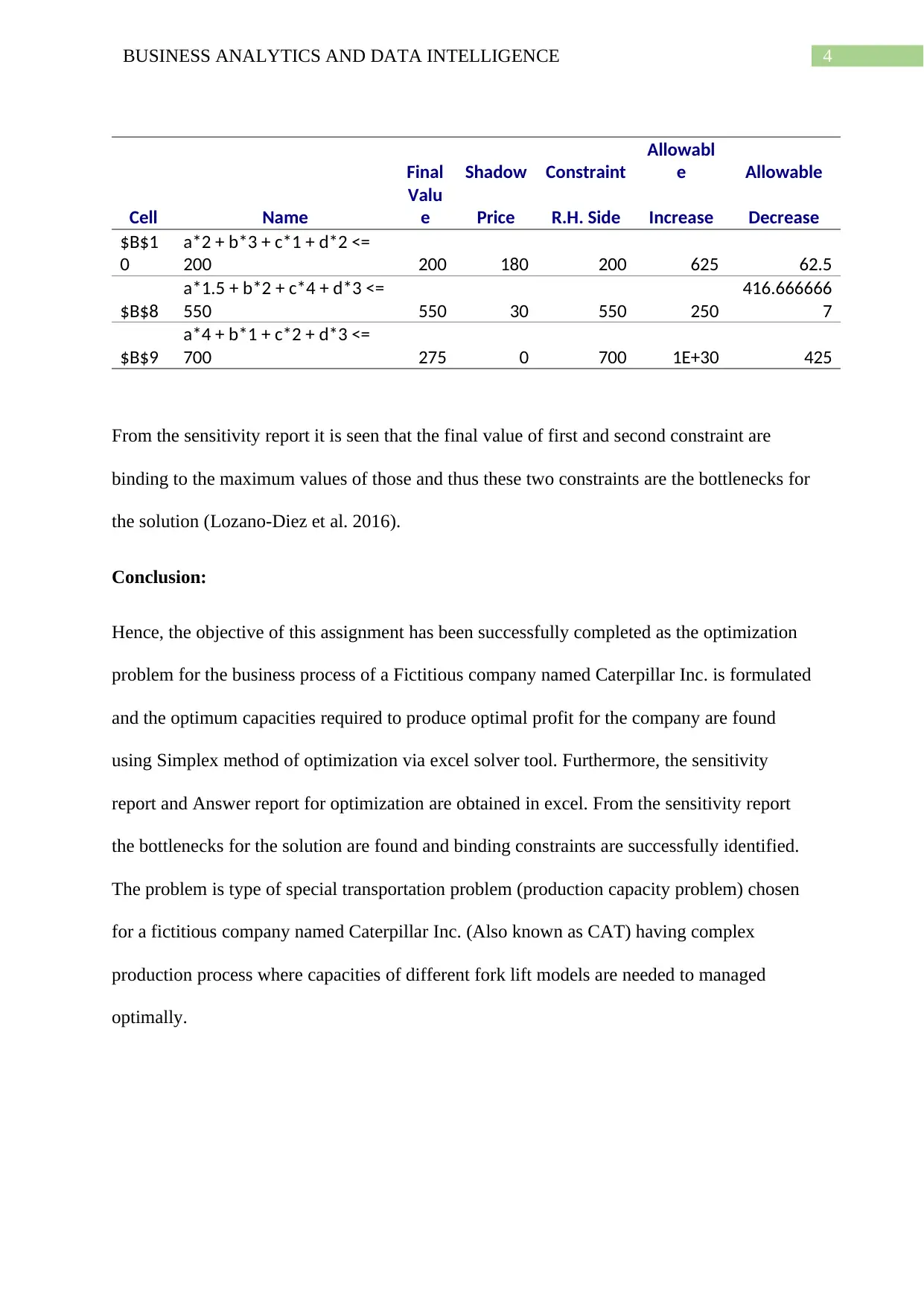
This project focuses on optimizing the production process of Caterpillar Inc. (CAT) using business analytics techniques. The assignment formulates an optimization problem with the objective of maximizing CAT's profit by determining the optimal production quantities of four forklift models (W1, W2, W3, and W4) across three assembly stages. The problem is solved using Excel Solver, employing the Simplex method to find the values of the decision variables that maximize the objective function, considering constraints related to assembly hours. The solution reveals the optimal production mix and the maximum achievable profit. A sensitivity report is also analyzed to identify the binding constraints and potential bottlenecks in the production process. The project successfully demonstrates the application of optimization techniques to a real-world business scenario, providing insights into production capacity management and profit maximization. The assignment is a practical application of business analytics principles.

Running head: BUSINESS ANALYTICS AND DATA INTELLIGENCE
BUSINESS ANALYTICS AND DATA INTELLIGENCE
Name of the Student
Name of the University
Author Note

1BUSINESS ANALYTICS AND DATA INTELLIGENCE
Introduction:
In this particular assignment the optimization technique by excel solver is used to find the
optimum values of capacities that are needed to be used for a fictitious company named
Caterpillar Inc. The objective of the problem is to maximize the profit of Caterpillar Inc. by
optimal use of the capacities in the three departments. The four types of fork lift models that
are produced by CAT are W1,W2,W3 and W4 and each of the fork lift model give 400£,
600£, 300£ and 100£ profit to the company in one month (ALJASSER and Sasidhar 2018).
There are 3 stages in the process of the assembly which are stage 1, stage 2 and stage 3
assembly process. In the stage 1 assembly process maximum 550 hours per month can be
used. W1, W2, W3, W4 require 1.5,2,4 and 3 hours/unit in the stage 1 process. The stage 2
process is limited by 700 hours and the W1, W2, W3 and W4 require 4, 1, 2,1 hours/unit in
the stage 2 process. The stage 3 process is limited by monthly capacity of 200 hours and in
this stage W1,W2,W3 and W4 require 2,3,1,2 hours/unit respectively.
Optimization problem formulation and Solution:
Now, let a, b, c and d are the number of fork lift models of W1,W2,W3 and W4 respectively
and these will produce the maximum profit for CAT Inc.
Hence, the objective function will be
Maximize 400*a + 600*b + 300*c+ 100*d
The decision variables in the optimization problem are the variables with the optimum value
gives maximum profit. Hence, the number of fork lift models of W1, W2, W3 and W4 which
are a, b, c and d are the decision variables (Gonçalves et al. 2015).
Hence, the constraints of the system in equation form will be,

2BUSINESS ANALYTICS AND DATA INTELLIGENCE
a*1.5 + b*2 + c*4 + d*3 <= 550
a*4 + b*1 + c*2 + d*3 <= 700
a*2 + b*3 + c*1 + d*2 <= 200
The created spreadsheet for solving the maximization problem in solver is shown below.
Decision variables
a 0
b 25
c 125
d 0
Constraints
a*1.5 + b*2 + c*4 + d*3 <= 550 550
a*4 + b*1 + c*2 + d*3 <= 700 275
a*2 + b*3 + c*1 + d*2 <= 200 200
Objective function
Maximize 400*a + 600*b + 300*c+ 100*d 52500
Result:
Now, from the above table it is found that the maximum profit will be obtained when the
values of variable are a = 0, b= 25, c= 125 and d = 0. The maximum profit found using the
Simplex method in excel solver is 52500£.
Solver screenshot of optimization parameters:

3BUSINESS ANALYTICS AND DATA INTELLIGENCE
Hence, the number of fork lift models of W1,W2,W3 and W4 types for maximum profit are
0,25, 125 and 0 respectively.
Hence, it is recommended that for optimum (maximum) profit of CAT company is 52500 £ if
the types of numbers of fork lift models produced are 0 W1 models, 25 W2 models, 125 W3
models and 0 W4 models respectively (Zhao et al. 2015).
Sensitivity report:
Final
Reduce
d Objective
Allowabl
e Allowable
Cell Name
Valu
e Cost
Coefficien
t Increase Decrease
$B$2:$B$5
$B$2 a 0 -5 400 5 1E+30
$B$3 b 25 0 600 300
7.69230769
2
$B$4 c 125 0 300 900 100
$B$5 d 0 -350 100 350 1E+30

4BUSINESS ANALYTICS AND DATA INTELLIGENCE
Final Shadow Constraint
Allowabl
e Allowable
Cell Name
Valu
e Price R.H. Side Increase Decrease
$B$1
0
a*2 + b*3 + c*1 + d*2 <=
200 200 180 200 625 62.5
$B$8
a*1.5 + b*2 + c*4 + d*3 <=
550 550 30 550 250
416.666666
7
$B$9
a*4 + b*1 + c*2 + d*3 <=
700 275 0 700 1E+30 425
From the sensitivity report it is seen that the final value of first and second constraint are
binding to the maximum values of those and thus these two constraints are the bottlenecks for
the solution (Lozano-Diez et al. 2016).
Conclusion:
Hence, the objective of this assignment has been successfully completed as the optimization
problem for the business process of a Fictitious company named Caterpillar Inc. is formulated
and the optimum capacities required to produce optimal profit for the company are found
using Simplex method of optimization via excel solver tool. Furthermore, the sensitivity
report and Answer report for optimization are obtained in excel. From the sensitivity report
the bottlenecks for the solution are found and binding constraints are successfully identified.
The problem is type of special transportation problem (production capacity problem) chosen
for a fictitious company named Caterpillar Inc. (Also known as CAT) having complex
production process where capacities of different fork lift models are needed to managed
optimally.

5BUSINESS ANALYTICS AND DATA INTELLIGENCE
References:
Zhao, X., Qi, F., Yuan, C., Du, W. and Liu, D., 2015. Lipase-catalyzed process for biodiesel
production: enzyme immobilization, process simulation and optimization. Renewable and
Sustainable Energy Reviews, 44, pp.182-197.
ALJASSER, I.A. and Sasidhar, B., 2018. Scheduling in A Single-Stage, Multi-Item
Compatible Process Using Multiple ARC Network Model and Excel Solver. International
Review of Management and Business Research, 7(1), pp.23-31.
Gonçalves, C.A., de Almeida, M.A., Faria-Júnior, M.J.A., Pinto, M.F. and Garcia-Neto, M.,
2015. Accuracy of Nonlinear Formulation of Broiler Diets: Maximizing Profits. Brazilian
Journal of Poultry Science, 17(2), pp.173-180.
Lozano-Diez, A., Silnova, A., Matejka, P., Glembek, O., Plchot, O., Pešán, J., Burget, L. and
Gonzalez-Rodriguez, J., 2016. Analysis and optimization of bottleneck features for speaker
recognition. In Proceedings of Odyssey (Vol. 2016, pp. 352-357). ISCA Bilbao, Spain.