GB513: Business Analytics - Unit 3 Assignment on Hypothesis Testing

This document presents a comprehensive solution to a Business Analytics assignment, focusing on probability calculations and hypothesis testing. The solution includes detailed answers to questions involving z-values, t-tests, and the application of statistical concepts to real-world business scenarios. The assignment covers various aspects, including calculating probabilities based on normal distributions, hypothesis testing for population means and proportions, and the use of Excel for statistical analysis. The solution provides step-by-step calculations, null and alternative hypotheses, and conclusions based on p-values and significance levels. The assignment also involves interpreting the results of statistical tests and drawing meaningful conclusions about the data. The document provides a valuable resource for students studying business analytics, offering insights into the application of statistical methods in solving business problems.

Unit 3: Answers by (Name)

Answer 1
1 Z= 3
Answers 2
2a P= 0.98
2b P=0.68
Answers 3
3a P=0.22
3b P= 0.56
Answers 4
Null hypothesis: H0: ( μ=3 . 16 ) : Mean price of a “gallon gasoline in the United States” is $
3.16.
Alternative hypothesis: HA: ( μ≠3 . 16 ) : Mean price of a “gallon gasoline in the United States”
is significantly different from $ 3.16.
T value: t0.01, 24 = 1.647
Conclusion: The null hypothesis failed to get rejected at 1% level of significance as the p-value
is greater (“not less than”) the alpha level. There is not adequate statistical substantiation to
prove that price of gasoline per gallon in the USA is greater or less than the average price of
$3.16.

Answer 5
Null hypothesis: H0: ( P=0 . 47 ) : Proportion of “money news” received from newspaper is 0.47
for the CFOs.
Alternative hypothesis: HA: ( P≠0 . 47 ) : Proportion of “money news” received from newspaper
is significantly different from 0.47 for the CFOs.
Z-value: Z –calculated = 1.05
Conclusion: The null hypothesis failed to get rejected at 5% level as the calculated Z-value was
smaller than the critical Z-value, and was in the acceptance region. There is not adequate
statistical substantiation to conclude that percentage of people receiving “money news” from
newspaper is any different from 47%.
Answer 6
Null hypothesis: H0: ( μm =μw ) : Average spending of men for “Valentine’s Day gift” is same
with average spending of the women.
Alternate hypothesis: HA: ( μm > μw ) : On an average, men spend significantly more compared
to average spending of the women for “Valentine’s Day gift”.
P or t value: t0. 01 , 22=1. 72 with p-value = 0.052 > 0.01
Conclusion: The null hypothesis failed to get rejected at alpha = 0.01 level, as the p-value is
greater than the alpha level. There is not enough adequate statistical substantiation to conclude
that any significant dissimilarity existed between average spending of men and women for

Valentine’s Day gift. Therefore, on an average, men spend almost same amount of money for
“Valentine’s Day gift” compared to women.
Work
Question 1
Let X = “Marks in Exam”, where ‘X’ ~ N ( μ = 75 and σ = 10)
According to the problem X = 105
The standard normal variable is calculated as Z = (X - μ )/ σ
So, Z = (105 – 75)/ 10 = 3
Hence, P (X = 105) = P (Z = 3)
Therefore, we have to look for Z = 3 in the standard normal table.
Question 2
According to the problem, X = “Monthly household cellular phone bill”, where ‘X’ ~ N ( μ = $
73 and σ =$ 11).
a. Required probability of any selected monthly cellular bill will be less than $ 95 = P (X <
95)
The standard normal variable is calculated as Z = (X - μ )/ σ
Now, X = $ 95 => Z = (95 – 73) / 11 = 2
So, P (X < 95) = P (Z < 2) = 0.9772 = 0.98 (using standard normal table).
b. Required probability of any selected monthly cellular bill will be greater than $ 62 and
less than $ 84 = P (62 < X < 84)

Now, X = $ 62 => Z = (62 – 73) / 11 = -1, and X = $ 84 => Z = (84 – 73) / 11 = 1.
So, P (62 < X < 84) = P (-1 < Z < 1) = 2* P (0 < Z < 1) (as normal curve is symmetric)
Hence, P (62 < X < 84) = 2* P (0 < Z < 1) = 2 * 0.3413 = 0.6826 = 0.68 (using standard
normal table).
Question 3
Sample size N = 950, and proportion of response about internal company visit = 19% => P =
0.19.
a. Here required response from business travellers about their trip being internal company
visit is more than 20%.
Let p = “Proportion of business travellers saying that their last visit was a internal
company visit”.
The standard normal variable is calculated as Z = (p - P)/ σ
Here,
σ = √ P ( 1−P )
N = √ 0 . 19∗( 1−0 .19 )
950 = 0.013
So, required probability is calculated as, P (p > 0.2) = P (Z > (0.2 – 0.19) / 0.013) = P (Z
> 0.77)
Now, P (Z > 0.77) = 1 – P (Z ≤ 0.77) = 1 – 0.7794 = 0.2206 = 0.22 (using standard
normal table).
b. Probability that the ratio of people saying recent business trip as internal visit lies
between 18% and 20% is = P (0.18 < p < 0.2)

So, required probability is calculated as, P (0.18 < p < 0.2) = P ((0.18 – 0.19) / 0.013) < Z
< (0.2 – 0.19) / 0.013) = P (- 0.77 < Z < 0.77) = 2* P (0 < Z < 0.77) = 2* 0.2794 = 0.5587
= 0.56 (using standard normal table).
Question 4
Let X = “price for a gallon self-serve regular unleaded gasoline”, which is normally distributed
with μ = $ 3.16.
Number of gasoline stations surveyed N = 25
The problem is to test the hypothesis that average price of a “gallon of gasoline” is $ 3.16 at
alpha = 0.01.
Null hypothesis: H0: ( μ=3 . 16 ) : Mean price of a “gallon gasoline in the United States” is $
3.16.
Alternate hypothesis: HA: ( μ≠3 . 16 ) : Mean price of a “gallon gasoline in the United States” is
significantly different from $ 3.16.
Level of significance: α = 0.01
Choice of test: One sample t-test (as standard deviation of price for population not available).
Test Statistics: Sample mean = X
¿
= 80.04 / 25 = 3.2
Sample SD = s = √ ∑ ( Xi−X
¿
) 2
N−1 = √ 0 . 3828
24 = 0.126 = 0.13

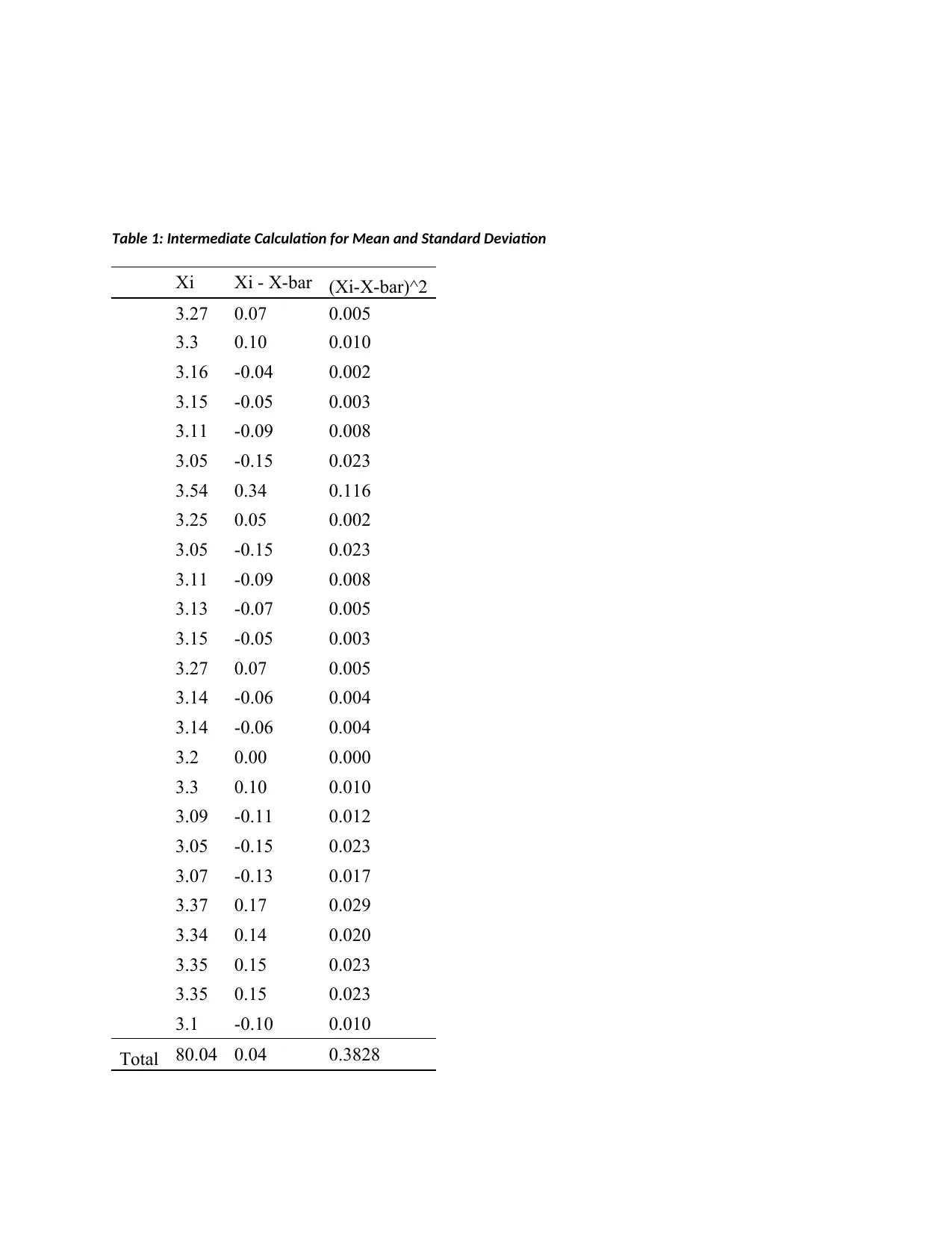
Table 1: Intermediate Calculation for Mean and Standard Deviation
Xi Xi - X-bar (Xi-X-bar)^2
3.27 0.07 0.005
3.3 0.10 0.010
3.16 -0.04 0.002
3.15 -0.05 0.003
3.11 -0.09 0.008
3.05 -0.15 0.023
3.54 0.34 0.116
3.25 0.05 0.002
3.05 -0.15 0.023
3.11 -0.09 0.008
3.13 -0.07 0.005
3.15 -0.05 0.003
3.27 0.07 0.005
3.14 -0.06 0.004
3.14 -0.06 0.004
3.2 0.00 0.000
3.3 0.10 0.010
3.09 -0.11 0.012
3.05 -0.15 0.023
3.07 -0.13 0.017
3.37 0.17 0.029
3.34 0.14 0.020
3.35 0.15 0.023
3.35 0.15 0.023
3.1 -0.10 0.010
Total 80.04 0.04 0.3828

Calculated t value: Hence, t0.01, 24 =
X
¿
−μ
s
√ N =
3 . 2−3 . 16
0 .13
√ 25 = 1.647 = 1.65
The p-value is P (|t| > 1.65) = 0.113 > 0.01
Decision: The null hypothesis failed to get rejected at 1% level of significance as the p-value is
greater than the alpha level (“level of significance”).
Conclusion: There is not adequate statistical substantiation to prove that price of gasoline per
gallon in the USA is different from $ 3.16.
Question 5
Let p = “percentage of money news from newspaper”, with P = 0.47, and assumed to be
normally distributed (Wang, 2010).
Number of surveyed CFOs “n” = 76
The problem is to test the null hypothesis that proportion of money news from newspaper is 0.47
at 5% level of significance.
Null hypothesis: H0: ( P=0 . 47 ) : Proportion of “money news” received from newspaper is 0.47
for the CFOs.
Alternate hypothesis: HA: ( P≠0 . 47 ) : Proportion of “money news” received from newspaper is
significantly different from 0.47 for the CFOs.
Level of significance: α = 0.05

Choice of test: Z-test for one sample proportion
Test Statistics: Sample proportion of CFOs receiving money news from newspaper is = p = 40 /
76 = 0.53.
Calculated z value: Hence, Z –calculated=
p−P
√ P ( 1−P )
n =
0. 53−0. 47
√ 0 . 47∗0 .53
76 = 1.048 = 1.05
Z-critical = ±1.645 at 5% level of significance (Gerstman, 2019).
|Z|-calculated < |Z|-critical, and the p-value P (|Z| > 1.05) = 0.295 > 0.05
Decision: The null hypothesis failed to get rejected at 5% level, as the p-value is greater (“not
less”) than the alpha level (De Winter, 2013).
Conclusion: There is not adequate statistical substantiation to conclude that percentage of people
receiving “money news” from newspaper is any different from 47%. Therefore, Robert Half
International was providing correct information.
Question 6
Problem: Evaluate the difference in money spend between men and women for Valentine’s Day
gift, which is noted to be normally distributed. The related hypothesis is tested using MS “Excel
Data Analysis Tool pack” (De Winter, 2013).
Null hypothesis: H0: ( μm =μw ) : There is no inequality between average spending of men and
women for “Valentine’s Day gift”.
Alternate hypothesis: HA: ( μm > μw ) : On an average, men spend significantly more compared
to that of the women for “Valentine’s Day gift”.

Level of significance: α = 0.01
Test statistics: Calculated p or t value:
The “two sample t-test with equal variances” is evaluated from the excel output as t0. 01 , 22=1. 72
with p-value = 0.052 > 0.01
Decision: The null hypothesis failed to get rejected at alpha = 0.01 level, where p-value is greater
the alpha level.
Conclusion: There is not adequate statistical substantiation to conclude that there is any
significant difference between average spending of men and women for “Valentine’s Day gift”.
Therefore, on an average, men spend almost equal money for “Valentine’s Day gift” compared
to women.
Table 2: Excel output of two sample t-Test assuming equal variances

References
De Winter, J. C. (2013). Using the Student's t-test with extremely small sample sizes. Practical
Assessment, Research & Evaluation, 18(10).
Gerstman, B. (2019). Standard Normal Table. Retrieved 6 August 2019, from
http://www.sjsu.edu/faculty/gerstman/EpiInfo/z-table.htm.
Wang, W. (2010). On construction of the smallest one-sided confidence interval for the
difference of two proportions. The Annals of Statistics, 38(2), 1227-1243.