Business Data Analysis Assignment - Higher Diploma in Data Analytics

This assignment solution addresses a Business Data Analysis exam from the National College of Ireland, covering multiple statistical methods. Question one involves a paired t-test to compare contestant weights before and after a weight-loss program, including hypothesis formulation, test statistic calculation, error probability specification, and result interpretation. Question two presents an unpaired t-test to determine if there's a significant difference between the test scores of two classes, detailing hypothesis testing, test statistic calculation, error probability, and decision-making. Question three utilizes one-way ANOVA to analyze the difference between three training methods, covering hypothesis, F-statistic calculation, error probability specification, and result interpretation. Question four explores Chi-square to analyze road traffic accident data and time series analysis using moving average and exponential smoothing to forecast stock prices. The solution provides detailed calculations and interpretations for each question.

Student Name
Course Name
Institution Affiliation

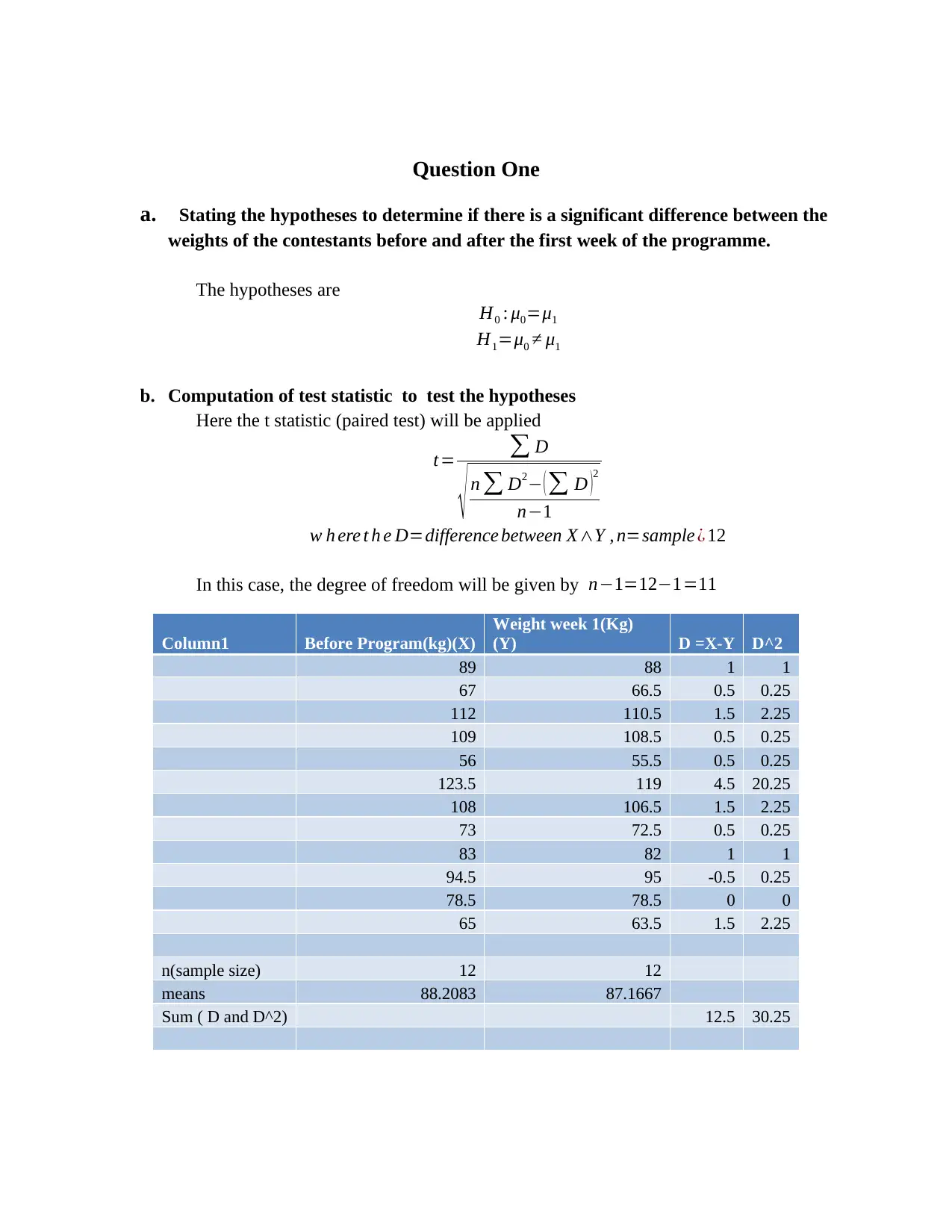
Question One
a. Stating the hypotheses to determine if there is a significant difference between the
weights of the contestants before and after the first week of the programme.
The hypotheses are
H0 : μ0=μ1
H1=μ0 ≠ μ1
b. Computation of test statistic to test the hypotheses
Here the t statistic (paired test) will be applied
t= ∑ D
√ n ∑ D2− ( ∑ D )
2
n−1
w h ere t h e D=difference between X∧Y , n=sample ¿ 12
In this case, the degree of freedom will be given by n−1=12−1=11
Column1 Before Program(kg)(X)
Weight week 1(Kg)
(Y) D =X-Y D^2
89 88 1 1
67 66.5 0.5 0.25
112 110.5 1.5 2.25
109 108.5 0.5 0.25
56 55.5 0.5 0.25
123.5 119 4.5 20.25
108 106.5 1.5 2.25
73 72.5 0.5 0.25
83 82 1 1
94.5 95 -0.5 0.25
78.5 78.5 0 0
65 63.5 1.5 2.25
n(sample size) 12 12
means 88.2083 87.1667
Sum ( D and D^2) 12.5 30.25

Therefore,
t= 12.5
√ 12 ( 30.5 )−12.52
12−1
= 12.5
√ 363−156.25
11
¿ 12.5
√ 206.75
11
= 12.5
4.3354
¿ 2.8833
Hence, tcomputed=2.8833
c. Specification and justification of an appropriate probability for committing
Type I error (α)
The probability of committing type I error will be 5%, which is the probability of
incorrectly rejecting the null hypothesis. This will be attained at the significance level
of 95%, which is the probability of rejecting or accepting the null hypothesis
accurately.
To make the decision, in this case, the critical value of need to determine from
t-tables
t0.05 ( 11 df ) ( twotailed ) =1.796
d. Reporting of the decision and clearly explain your result.
The tcomputed=2.8833 ¿ tα =1.796 , therefore, null hypothesis, H0 t h e t h e t h e : μ0=μ1
is rejected. This suggest that there is significant difference between the weights
of the contestants before and after the first week of the programme .

In this case, alternative hypothesis H1=μ0 ≠ μ1 is accepted. In conclusion the
weight of the contestant is not the same before and after the programme, the t-
test conducted reveals this.
Question Two
a. Stating the hypotheses determine if there is a significant difference between the test
scores of both classes
The hypotheses to be determined are
H0 : μ0=μ1
H1=μ0 ≠ μ1
b. Calculation of test statistic to test the hypotheses
Due to an unequal sample size of the two variables, t-statistics (unpaired test), equal
variance, will be conducted.
t= ( X −Y )
√ ( sx
2
n1
+ sy
2
n2 )
where , sx
2∧s y
2 are the variance of X ∧Y respectively , X∧Y are the means of X
Y are the means of X∧Y respectively , n1∧n2 are the sample ¿ X a nd Y

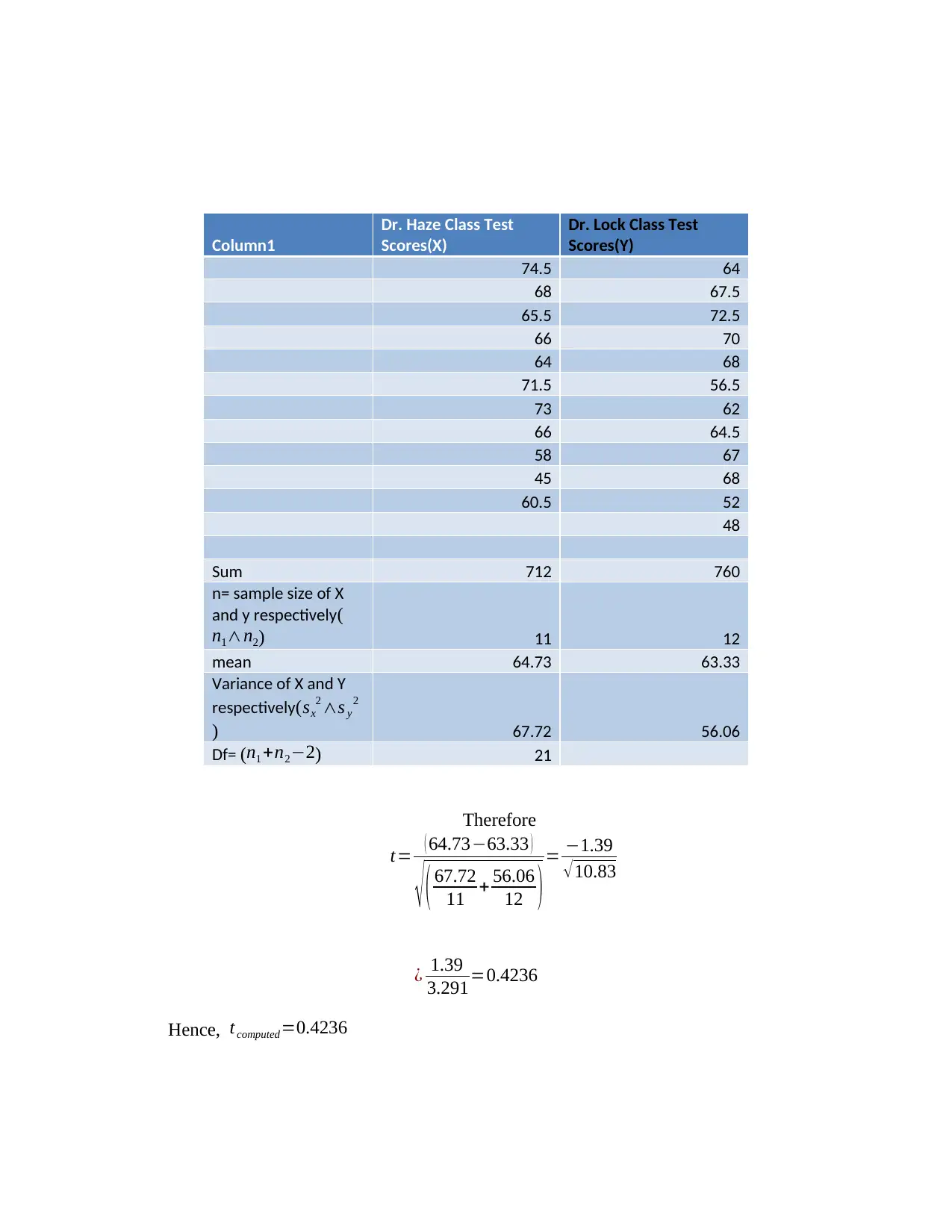
Column1
Dr. Haze Class Test
Scores(X)
Dr. Lock Class Test
Scores(Y)
74.5 64
68 67.5
65.5 72.5
66 70
64 68
71.5 56.5
73 62
66 64.5
58 67
45 68
60.5 52
48
Sum 712 760
n= sample size of X
and y respectively(
n1∧n2) 11 12
mean 64.73 63.33
Variance of X and Y
respectively( sx
2 ∧s y
2
) 67.72 56.06
Df= (n1 +n2−2) 21
Therefore
t= ( 64.73−63.33 )
√ ( 67.72
11 + 56.06
12 )= −1.39
√10.83
¿ 1.39
3.291=0.4236
Hence, tcomputed=0.4236

c. Specifying and justifying an appropriate probability of committing a
Type I error (α).
To make the decision critical value of t at 95% significance level from t-table is needed.
This will set the probability of incorrectly rejecting the null hypothesis at 5%, which is
the chance of committing type I error. This is a reasonable level at which the end results
of the statistical test are reasonable.
For the above case, the critical value of t at 95% significance level will be,
t0.05 (21 df ) ( twotailed )=1.721
d. Decision and clear explanation of the result
Since, tcomputed=0.4236 < critical value 1.721, null hypothesis H0 is accepted. This
indicates that there is no significant difference between the test scores of both classes, Dr
Haze Class Scores and Dr Lock Class Scores. This suggest that the student taking the
same statistical test from the two classes are likely to get similar results, the class
does not matter as revealed by the t-s statistic test results.

Question Three
a. Stating the hypotheses to determine if there is a significant difference between
the different methods of training
The hypotheses will be,
H0 : μ0=μ1 =μ2
H0 : μ0 ≠ μ1∨μ0 ≠ μ2∨μ1=μ2
The concern will be whether there are differences among the means of three methods of
training.
b. Calculation of test statistic to test the hypotheses
For the case above, one-way ANOVA is required, where F-statistic will be determined,
because the sample has more than two groups, has three. This involves comparison of
the between the groups and within the groups.
F=
SSb
Df b
SSW
Df W
= Mean Squareb etween
Mean Squarewithin
Within-group Sum of Square ( SSW )
SSW =∑
j=1
p
∑
i=1
n
( Xi , j −X j ) 2
where , Xi , j are theobservations ∈groups∧X j average of group J

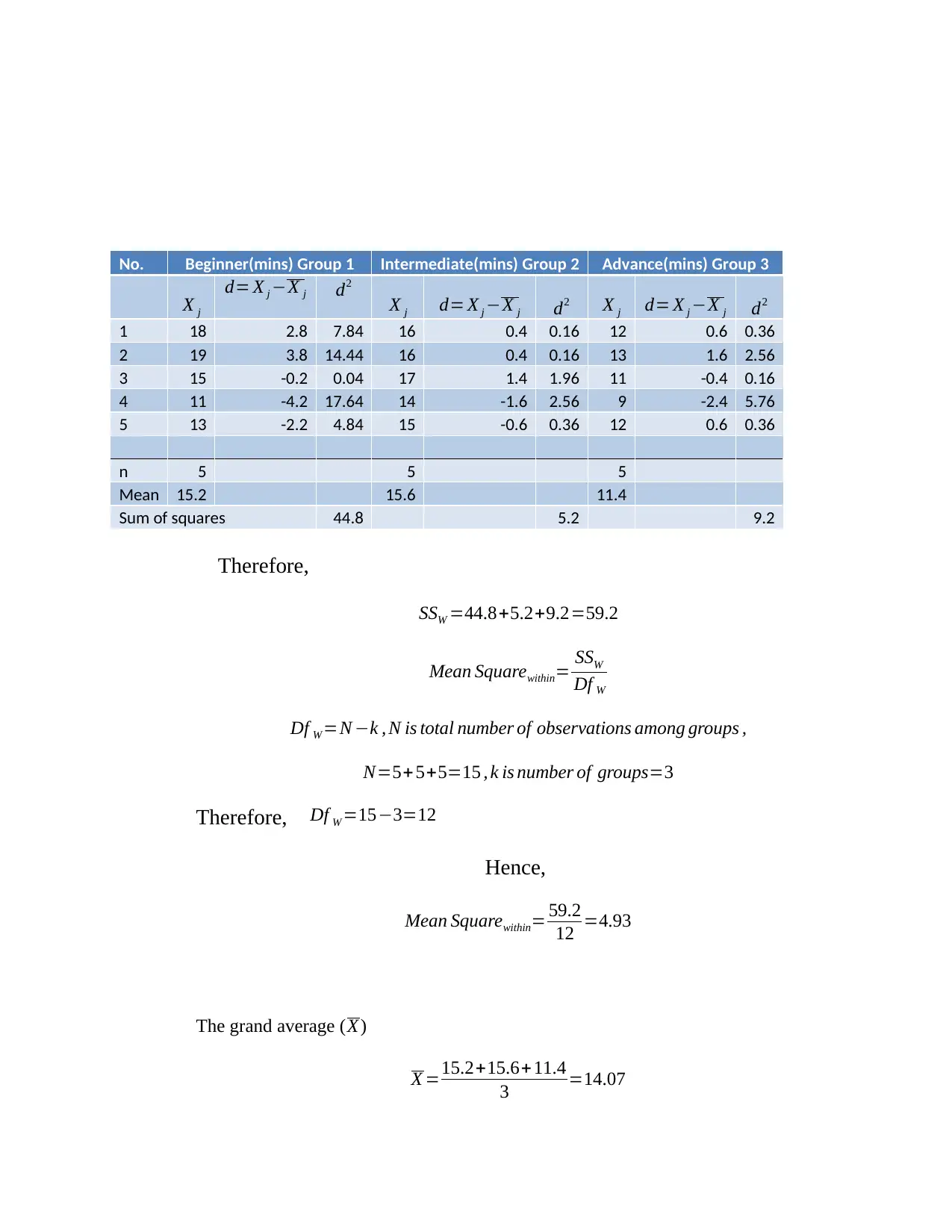
No. Beginner(mins) Group 1 Intermediate(mins) Group 2 Advance(mins) Group 3
X j
d= X j −X j d2
X j d= X j −X j d2 X j d= X j −X j d2
1 18 2.8 7.84 16 0.4 0.16 12 0.6 0.36
2 19 3.8 14.44 16 0.4 0.16 13 1.6 2.56
3 15 -0.2 0.04 17 1.4 1.96 11 -0.4 0.16
4 11 -4.2 17.64 14 -1.6 2.56 9 -2.4 5.76
5 13 -2.2 4.84 15 -0.6 0.36 12 0.6 0.36
n 5 5 5
Mean 15.2 15.6 11.4
Sum of squares 44.8 5.2 9.2
Therefore,
SSW =44.8+5.2+9.2=59.2
Mean Squarewithin= SSW
Df W
Df W =N −k , N is total number of observations among groups ,
N=5+ 5+5=15 , k is number of groups=3
Therefore, Df W =15−3=12
Hence,
Mean Squarewithin= 59.2
12 =4.93
The grand average ( X )
X =15.2+15.6+ 11.4
3 =14.07

Between-Group
Here Sum of Squares ( SSb) will be computed
SSb =n∑
j=1
p
( X j−X )2
where X j is average group J ∧ X is Grand average
SSb =5 (15.2−14.07 )2 +5 ( 15.6−14.07 )2+5 (11.4−14.07)2
¿ 6.42+11.76+35.56=53.73
Mean Squarebetween= SSb
Df b
Df b=k −1=3−1=2 , k is number of groups=3
Hence,
Mean Squarebetween=53.73
2 =26.87
Thus,
F=
SSb
Df b
SSW
Df W
= Mean Squarebetween
Mean Squarewithin
= 26.87
4.93
¿ 5.4459
Fcomputed=5.4459
c. The probability of committing type I error
To make the decision critical value of F at 95% significance level from F-table is needed.
This will set the probability of incorrectly rejecting the null hypothesis at 5%, which is
the chance of committing type I error. This is a reasonable level at which the end results
of the statistical test are reasonable.

For the above case, the critical value of F at 95% significance level will be,
Fα ( 2 ,12 df ) =3.89
a. Decision
d. Since
Fcomputed=5.4459 ¿ Fα=3.89 , the null hypothesis H0 : μ0=μ1 =μ2 will be rejected.
In this case, the alternative hypothesis accepted. This suggests that there is a
significant difference between the different methods of training. This means that
employees from different level will not complete a task within the same period
of time, some will spend more time, while others will take less time.
In conclusion, the time takes to complete a task depends on the method of training
the employee has undergone. This revealed by the test statistic conducted on the data.
Question Four
a. Road traffic data from Road Safety Authority
i. Stating the hypotheses to test if there is a difference
The hypotheses will be:
H0: There’s no difference
This leading to the determination of Expected results, for our case, all the days of
the will be said to have equal number of accidents, 11 accidents. This establishes
the claim there is no difference
H1: There’s difference

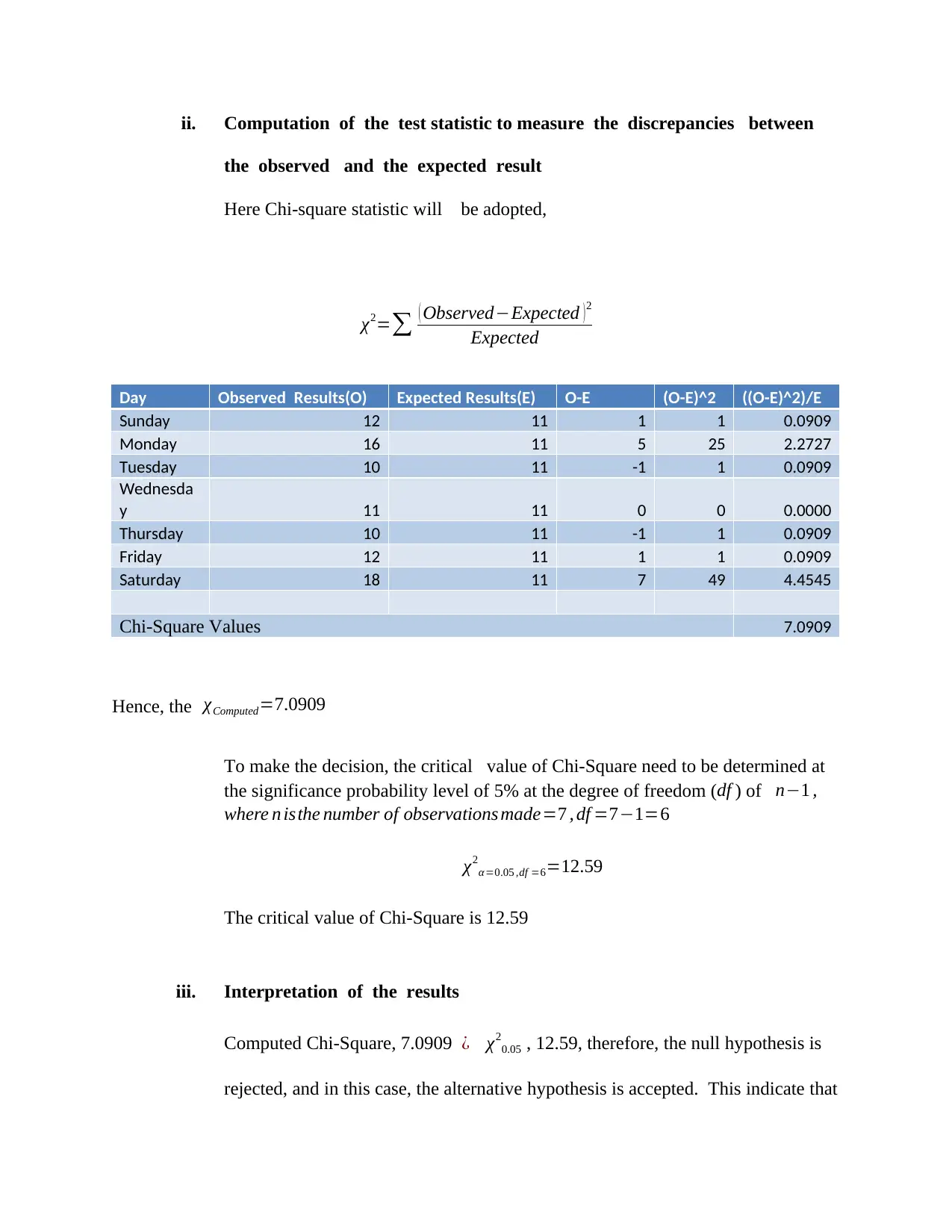
ii. Computation of the test statistic to measure the discrepancies between
the observed and the expected result
Here Chi-square statistic will be adopted,
χ2=∑ ( Observed−Expected )2
Expected
Day Observed Results(O) Expected Results(E) O-E (O-E)^2 ((O-E)^2)/E
Sunday 12 11 1 1 0.0909
Monday 16 11 5 25 2.2727
Tuesday 10 11 -1 1 0.0909
Wednesda
y 11 11 0 0 0.0000
Thursday 10 11 -1 1 0.0909
Friday 12 11 1 1 0.0909
Saturday 18 11 7 49 4.4545
Chi-Square Values 7.0909
Hence, the χComputed=7.0909
To make the decision, the critical value of Chi-Square need to be determined at
the significance probability level of 5% at the degree of freedom (df ) of n−1 ,
where n isthe number of observations made=7 , df =7−1=6
χ2
α =0.05 ,df =6=12.59
The critical value of Chi-Square is 12.59
iii. Interpretation of the results
Computed Chi-Square, 7.0909 ¿ χ2
0.05 , 12.59, therefore, the null hypothesis is
rejected, and in this case, the alternative hypothesis is accepted. This indicate that

there is a difference between the expected resulted and the observed results at
the significance probability level of 5%.
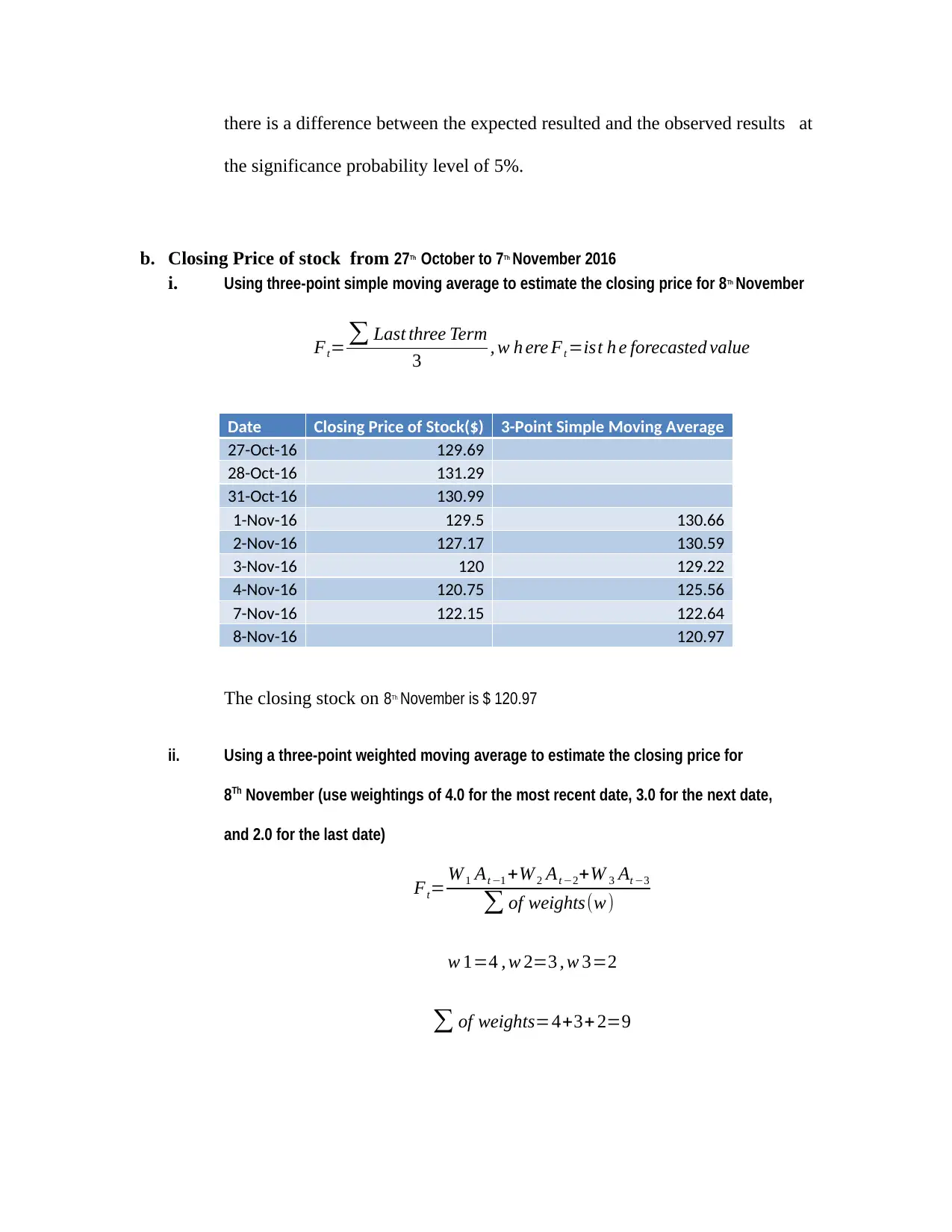
b. Closing Price of stock from 27Th October to 7Th November 2016
i. Using three-point simple moving average to estimate the closing price for 8Th November
Ft= ∑ Last three Term
3 , w h ere Ft =ist h e forecasted value
Date Closing Price of Stock($) 3-Point Simple Moving Average
27-Oct-16 129.69
28-Oct-16 131.29
31-Oct-16 130.99
1-Nov-16 129.5 130.66
2-Nov-16 127.17 130.59
3-Nov-16 120 129.22
4-Nov-16 120.75 125.56
7-Nov-16 122.15 122.64
8-Nov-16 120.97
The closing stock on 8Th November is $ 120.97
ii. Using a three-point weighted moving average to estimate the closing price for
8Th November (use weightings of 4.0 for the most recent date, 3.0 for the next date,
and 2.0 for the last date)
Ft= W 1 At −1 +W 2 At −2+W 3 At −3
∑ of weights(w)
w 1=4 , w 2=3 , w 3=2
∑ of weights=4+3+ 2=9