Report: Analyzing Normal Distribution in Business Mathematics
VerifiedAdded on 2021/05/31
|13
|1731
|374
Report
AI Summary
This report delves into the application of normal distribution within a business context, specifically analyzing electricity costs in a city. The study begins by calculating probabilities related to download times, demonstrating an understanding of z-scores and statistical inference. The core of the report focuses on the normal distribution, utilizing various statistical tools and techniques to assess the distribution of utility charges (electricity costs) for one-bedroom units. The analysis includes constructing and interpreting boxplots, histograms, and QQ-plots to determine the normality of the data. Summary statistics, including mean, median, skewness, and kurtosis, are calculated and discussed in relation to the data's distribution. The report also compares the data characteristics with theoretical assumptions of normal distribution, such as the 68-95-99.7 rule. Finally, the report concludes that the electricity costs are approximately normally distributed, with no extreme values, supported by the consistency of the results across the different analytical methods, including the normal table, histogram, and boxplot.

Mathematics for Business
Name
Course Number
Date
Faculty Name
Name
Course Number
Date
Faculty Name
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Mathematics for Business
PART A
The average download time is 2 seconds and a standard deviation of 0.5 seconds.
a) The probability that the download is above 1.8 seconds?
z−score= x−mean
standard deviation
1.8−2
0.5 =−0.4
The probability associated with the z-score value of -0.4 is less than 0.001. Therefore, the
probability of the download time being above 1.8 seconds is above 0.999.
b) The probability that the download is between 1.5 and 2.5
Z−scores= 1.5−2
0.5 <Z< 2.5−2
0.5
−1< Z<1
probability of Z ←1=0.1587
Probability of Z <1=0.8413
The probability of the download time is between 1.5 and 2.5 seconds is 0.8413−0.1587=0.6826
PART A
The average download time is 2 seconds and a standard deviation of 0.5 seconds.
a) The probability that the download is above 1.8 seconds?
z−score= x−mean
standard deviation
1.8−2
0.5 =−0.4
The probability associated with the z-score value of -0.4 is less than 0.001. Therefore, the
probability of the download time being above 1.8 seconds is above 0.999.
b) The probability that the download is between 1.5 and 2.5
Z−scores= 1.5−2
0.5 <Z< 2.5−2
0.5
−1< Z<1
probability of Z ←1=0.1587
Probability of Z <1=0.8413
The probability of the download time is between 1.5 and 2.5 seconds is 0.8413−0.1587=0.6826

c) 99% of the download times are slower than how many seconds?
Z score at 99 %=−2.33
−2.33= X−2
0.5
( 0.5∗−2.33 ) +2= X
X =2−1.165
0.835 seconds
PART B
Z score at 99 %=−2.33
−2.33= X−2
0.5
( 0.5∗−2.33 ) +2= X
X =2−1.165
0.835 seconds
PART B
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Introduction
Normal distribution is among the most used distributions in statistics. Their distribution
can be in different formats based on the mean and standard deviation. These statistics determine
the position and the shape. A widely distributed population has a normal distribution which has a
large kurtosis and longer tails. In addition, a population whose values are not approximately
distributed around the mean has a skewness statistic which is not equivalent to zero1. A negative
and positive skew indicates that the left and right tail are longer respectively – hence the mean
and median statistics are not equal. Therefore, using lower and higher moments of statistics, the
distribution of data can be effectively described. In a normally distributed population, respective
probability values can be estimated using the standard normal and inverse standard normal
tables2. There are various theoretical assumptions which can be used in determining whether a
sample is skewed or approximately normal. Also, boxplots, histograms and QQ-plots can be used
to check normality. In this paper, we will use the standard normal table, boxplot, histogram and
QQ-plot to check for normality of utility charges (electricity costs) of one-bedroom units in a
certain city.
Results & Discussions
a) Constructing Boxplot
Table 1: Summary statistics of Utility charges (Electricity costs)
Utility Charge (Electricity Costs)
Mean 147.06
Standard Error 4.482
Median 148.5
Mode 130
Standard Deviation 31.691
Sample Variance 1004.343
Kurtosis -0.544
1 Abdal-sahib et al., “Testing for Normality.”
2 Fletcher, “Normal Distribution.”
Normal distribution is among the most used distributions in statistics. Their distribution
can be in different formats based on the mean and standard deviation. These statistics determine
the position and the shape. A widely distributed population has a normal distribution which has a
large kurtosis and longer tails. In addition, a population whose values are not approximately
distributed around the mean has a skewness statistic which is not equivalent to zero1. A negative
and positive skew indicates that the left and right tail are longer respectively – hence the mean
and median statistics are not equal. Therefore, using lower and higher moments of statistics, the
distribution of data can be effectively described. In a normally distributed population, respective
probability values can be estimated using the standard normal and inverse standard normal
tables2. There are various theoretical assumptions which can be used in determining whether a
sample is skewed or approximately normal. Also, boxplots, histograms and QQ-plots can be used
to check normality. In this paper, we will use the standard normal table, boxplot, histogram and
QQ-plot to check for normality of utility charges (electricity costs) of one-bedroom units in a
certain city.
Results & Discussions
a) Constructing Boxplot
Table 1: Summary statistics of Utility charges (Electricity costs)
Utility Charge (Electricity Costs)
Mean 147.06
Standard Error 4.482
Median 148.5
Mode 130
Standard Deviation 31.691
Sample Variance 1004.343
Kurtosis -0.544
1 Abdal-sahib et al., “Testing for Normality.”
2 Fletcher, “Normal Distribution.”
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Skewness 0.016
Range 131
Minimum 82
1st quartile 126
3rd Quartile 168.75
Maximum 213
Sum 7353
Count 50
0
20
40
60
80
100
120
140
160
180
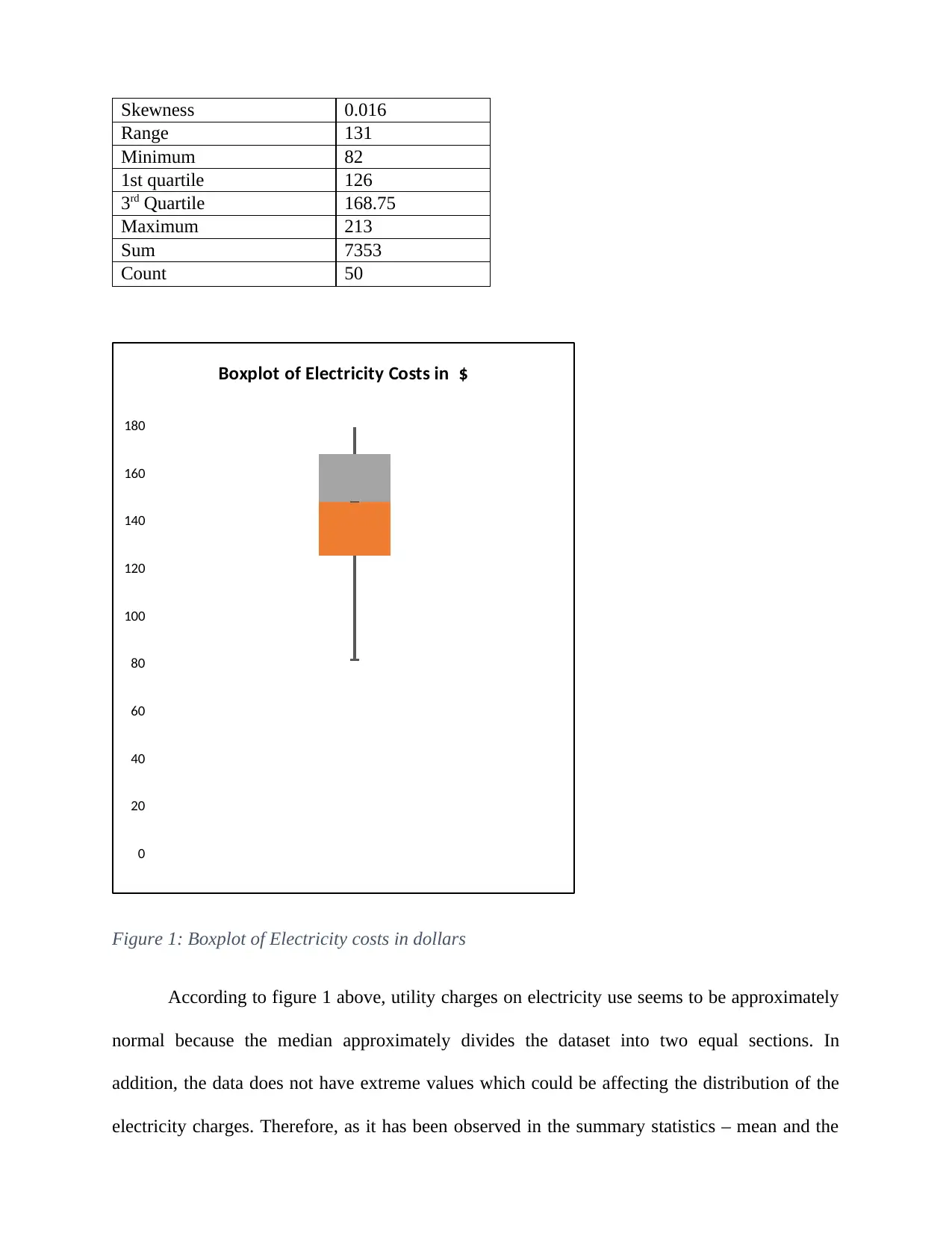
Boxplot of Electricity Costs in $
Figure 1: Boxplot of Electricity costs in dollars
According to figure 1 above, utility charges on electricity use seems to be approximately
normal because the median approximately divides the dataset into two equal sections. In
addition, the data does not have extreme values which could be affecting the distribution of the
electricity charges. Therefore, as it has been observed in the summary statistics – mean and the
Range 131
Minimum 82
1st quartile 126
3rd Quartile 168.75
Maximum 213
Sum 7353
Count 50
0
20
40
60
80
100
120
140
160
180
Boxplot of Electricity Costs in $
Figure 1: Boxplot of Electricity costs in dollars
According to figure 1 above, utility charges on electricity use seems to be approximately
normal because the median approximately divides the dataset into two equal sections. In
addition, the data does not have extreme values which could be affecting the distribution of the
electricity charges. Therefore, as it has been observed in the summary statistics – mean and the
median values are close to each other, the boxplot affirms the data is approximately normally
distributed.
b) Constructing Histogram
Table2: Histogram frequency table
Unsorted Bin Frequenc
y
Cumulative % Sorted
Bin
Frequenc
y
Cumulative %
80 0 0% 150 8 16%
90 2 4% 130 6 28%
100 2 8% 160 5 38%
110 3 14% 170 5 48%
120 4 22% 120 4 56%
130 6 34% 180 4 64%
140 3 40% 110 3 70%
150 8 56% 140 3 76%
160 5 66% 190 3 82%
170 5 76% 90 2 86%
180 4 84% 100 2 90%
190 3 90% 200 2 94%
200 2 94% 210 2 98%
210 2 98% 220 1 100%
220 1 100% 80 0 100%
More 0 100% More 0 100%
distributed.
b) Constructing Histogram
Table2: Histogram frequency table
Unsorted Bin Frequenc
y
Cumulative % Sorted
Bin
Frequenc
y
Cumulative %
80 0 0% 150 8 16%
90 2 4% 130 6 28%
100 2 8% 160 5 38%
110 3 14% 170 5 48%
120 4 22% 120 4 56%
130 6 34% 180 4 64%
140 3 40% 110 3 70%
150 8 56% 140 3 76%
160 5 66% 190 3 82%
170 5 76% 90 2 86%
180 4 84% 100 2 90%
190 3 90% 200 2 94%
200 2 94% 210 2 98%
210 2 98% 220 1 100%
220 1 100% 80 0 100%
More 0 100% More 0 100%
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 More
0
1
2
3
4
5
6
7
8
9
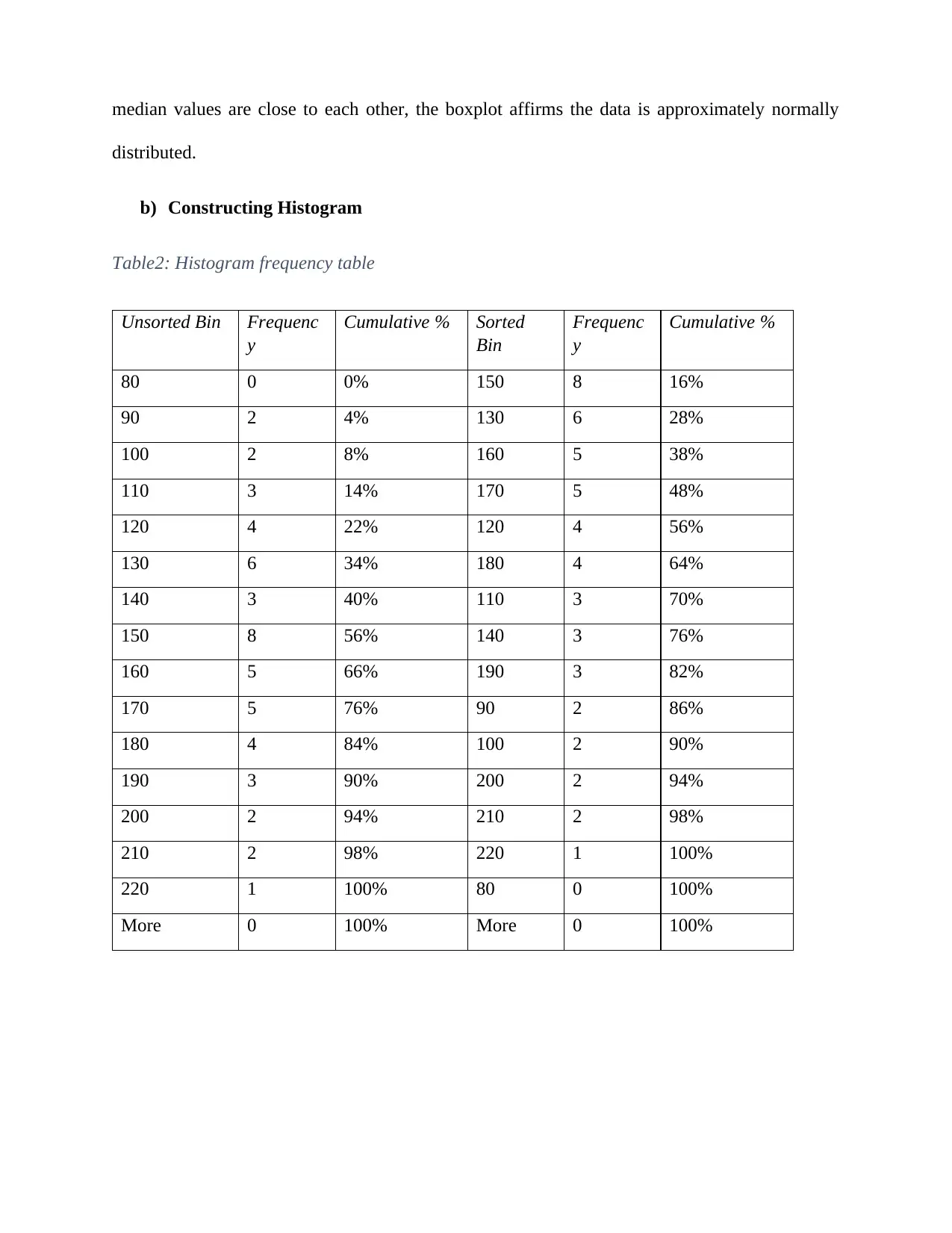
Histogram of Utility Charges (Electricity Costs)
Frequency
Figure 2: Unsorted Histogram of Utility Charges (Electricity costs)
Figure 2 above is a histogram chart with values of the electricity costs for the people in the city.
The histogram was plotted by using bins with differences of 10 from 80 to 220. The selection of
the bins was guided by the minimum and the maximum values. Most of the electricity bills were
between 140 and 140 dollars which had a frequency of 8 one-bedroomed apartments. According
to the distribution of the frequency in the histogram table and chart above, we can confirm that
the data is approximately equally distributed around the arithmetic mean3.
3 Scott, “Histogram.”
0
1
2
3
4
5
6
7
8
9
Histogram of Utility Charges (Electricity Costs)
Frequency
Figure 2: Unsorted Histogram of Utility Charges (Electricity costs)
Figure 2 above is a histogram chart with values of the electricity costs for the people in the city.
The histogram was plotted by using bins with differences of 10 from 80 to 220. The selection of
the bins was guided by the minimum and the maximum values. Most of the electricity bills were
between 140 and 140 dollars which had a frequency of 8 one-bedroomed apartments. According
to the distribution of the frequency in the histogram table and chart above, we can confirm that
the data is approximately equally distributed around the arithmetic mean3.
3 Scott, “Histogram.”
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
150 130 160 170 120 180 110 140 190 90 100 200 210 220 80 More
0
1
2
3
4
5
6
7
8
9
0%
20%
40%
60%
80%
100%
120%
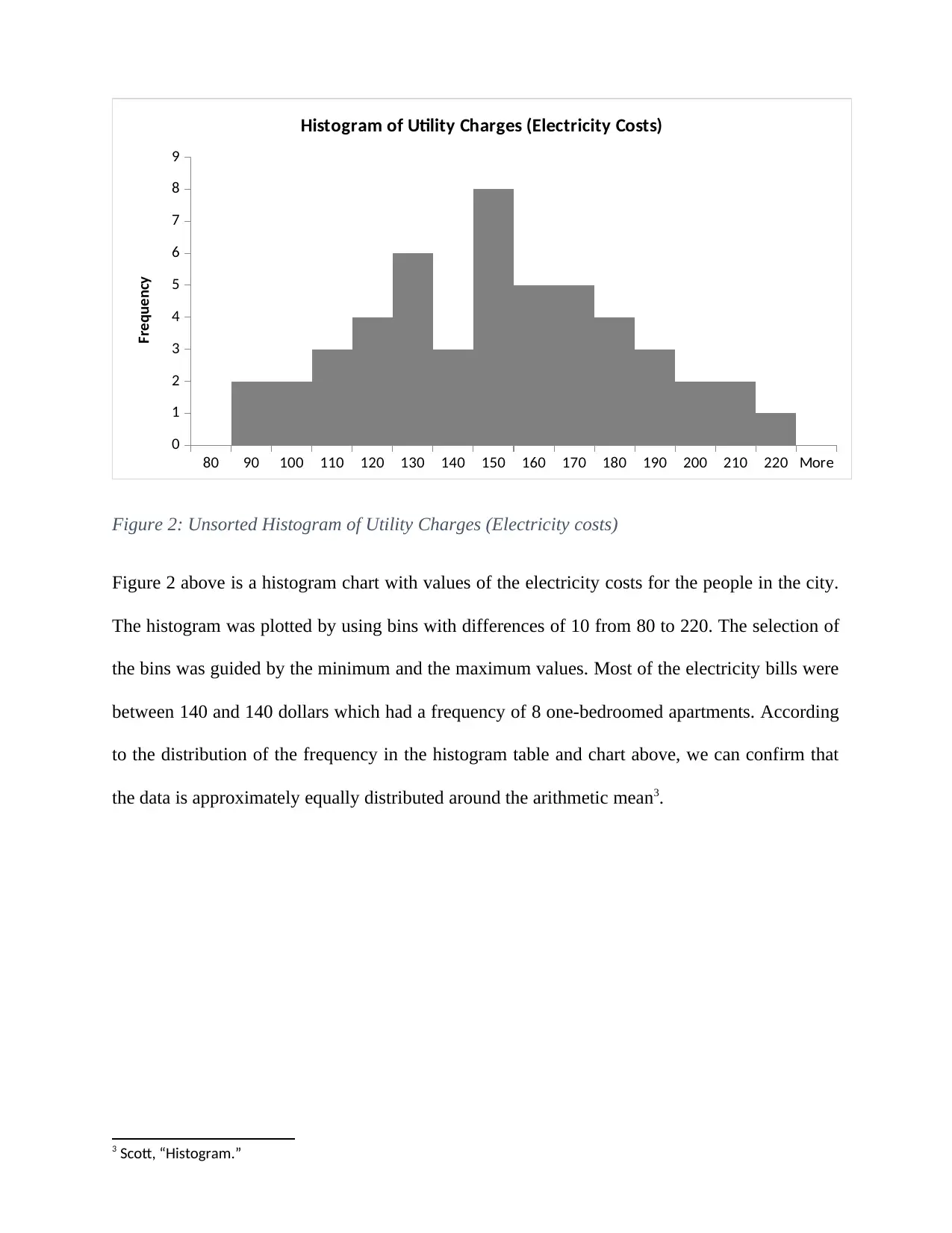
Sorted Histogram with Cumulative Percentage
Frequency Cumulative %
Frequency
Figure 3: Sorted Histogram with Cumulative frequencies
The sorted histogram above represents the bins in a chart from the one with the highest
frequency to the least. One-bedroom units in the 150, 130, 160, 170, 120 and 180 categories
cover 56% of the entire sample. 220 category had the least frequency and 150 had the highest.
c) Data Characteristics and Theoretical Properties
On average, the amount (in dollars) a resident in the city pays for the electricity is 147.06 dollars
with a standard deviation of 31.691 dollars. There is no much difference between the average
value and the median, indicating that the data is not highly skewed, hence approximately
normally distributed. Based on the skewness statistics which is 0.016, we can conclude the data
is slightly skewed to the right. The kurtosis is less than three hence concluding that the
distribution has less extreme values as compared to the standard normal distribution, hence the
0
1
2
3
4
5
6
7
8
9
0%
20%
40%
60%
80%
100%
120%
Sorted Histogram with Cumulative Percentage
Frequency Cumulative %
Frequency
Figure 3: Sorted Histogram with Cumulative frequencies
The sorted histogram above represents the bins in a chart from the one with the highest
frequency to the least. One-bedroom units in the 150, 130, 160, 170, 120 and 180 categories
cover 56% of the entire sample. 220 category had the least frequency and 150 had the highest.
c) Data Characteristics and Theoretical Properties
On average, the amount (in dollars) a resident in the city pays for the electricity is 147.06 dollars
with a standard deviation of 31.691 dollars. There is no much difference between the average
value and the median, indicating that the data is not highly skewed, hence approximately
normally distributed. Based on the skewness statistics which is 0.016, we can conclude the data
is slightly skewed to the right. The kurtosis is less than three hence concluding that the
distribution has less extreme values as compared to the standard normal distribution, hence the

peak is sharper. An individual who pays the highest amount of electricity cost in the city pays
around 213 dollars. In the same way, the least amount paid based on the sample was 82 dollars.
The interquartile range is 42.75, which is approximately equal to the theoretical assumption that
it should be 1.33 times the standard deviation (42.15). The range statistic for the one-bedroom
electricity costs is 131 and the theoretical assumption that it should be 6 times the standard
deviation has not been met (6 times of standard deviation is 190.146). There are 34 values
between negative and positive 1 standard score, which translate to 68%, hence the theoretical
assumption is met. 40 values lie between negative and positive 1.28 which is 80% as defined in
the normality theory. There are 48 values between negative and positive 2 which translates to
96%, hence the confirmation according to standard normal assumptions4.
d) Quantile-Quantile Normal Probability Plot
Table 3: Cumulative Distribution Function and Standardized Values
i Utility Charge CDF Z- Score Standardized Values
1 82 0.01 -2.32635 -65.06
2 90 0.03 -1.88079 -57.06
3 95 0.05 -1.64485 -52.06
4 96 0.07 -1.47579 -51.06
5 102 0.09 -1.34076 -45.06
6 108 0.11 -1.22653 -39.06
7 109 0.13 -1.12639 -38.06
8 111 0.15 -1.03643 -36.06
4 Fletcher, “Normal Distribution.”
around 213 dollars. In the same way, the least amount paid based on the sample was 82 dollars.
The interquartile range is 42.75, which is approximately equal to the theoretical assumption that
it should be 1.33 times the standard deviation (42.15). The range statistic for the one-bedroom
electricity costs is 131 and the theoretical assumption that it should be 6 times the standard
deviation has not been met (6 times of standard deviation is 190.146). There are 34 values
between negative and positive 1 standard score, which translate to 68%, hence the theoretical
assumption is met. 40 values lie between negative and positive 1.28 which is 80% as defined in
the normality theory. There are 48 values between negative and positive 2 which translates to
96%, hence the confirmation according to standard normal assumptions4.
d) Quantile-Quantile Normal Probability Plot
Table 3: Cumulative Distribution Function and Standardized Values
i Utility Charge CDF Z- Score Standardized Values
1 82 0.01 -2.32635 -65.06
2 90 0.03 -1.88079 -57.06
3 95 0.05 -1.64485 -52.06
4 96 0.07 -1.47579 -51.06
5 102 0.09 -1.34076 -45.06
6 108 0.11 -1.22653 -39.06
7 109 0.13 -1.12639 -38.06
8 111 0.15 -1.03643 -36.06
4 Fletcher, “Normal Distribution.”
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
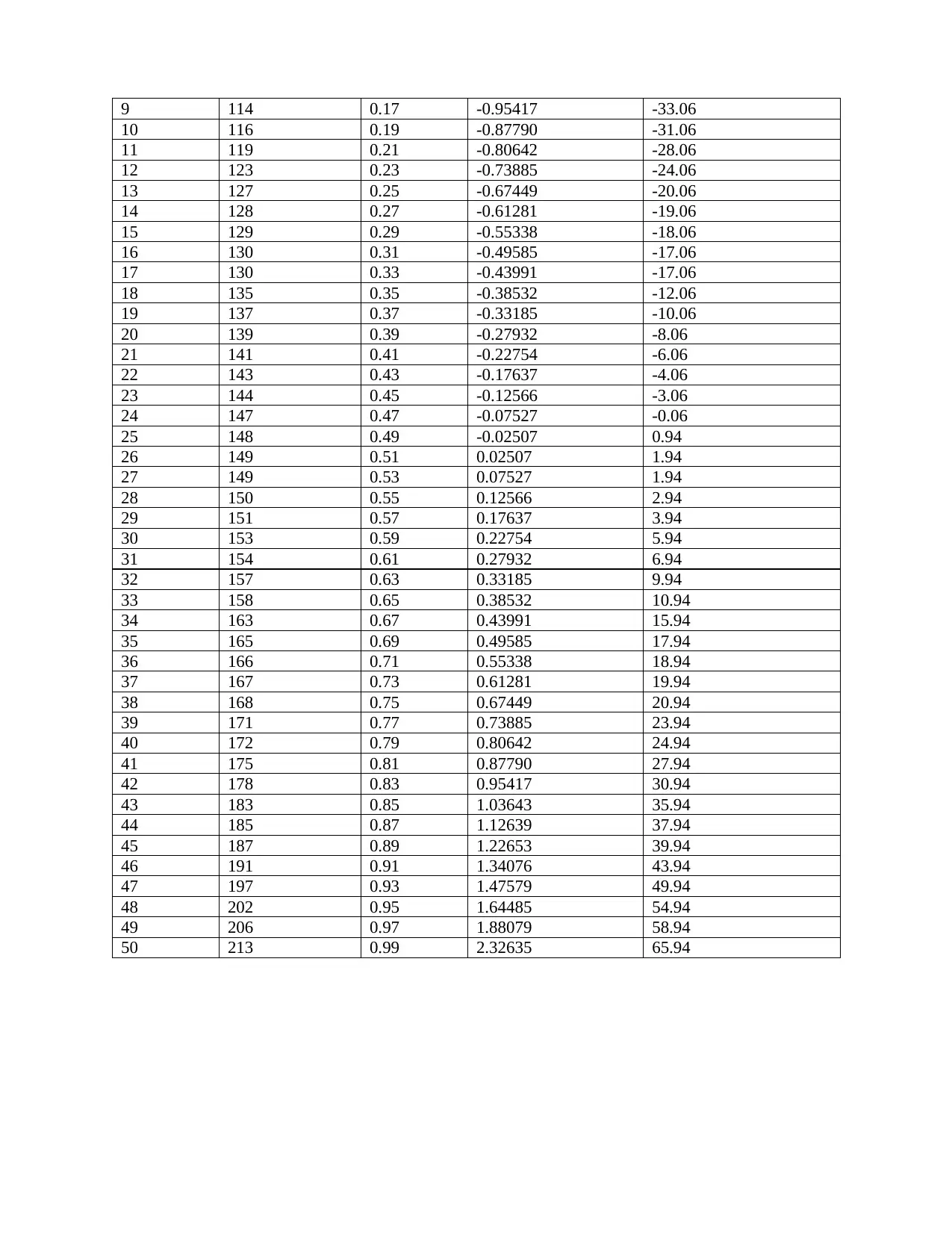
9 114 0.17 -0.95417 -33.06
10 116 0.19 -0.87790 -31.06
11 119 0.21 -0.80642 -28.06
12 123 0.23 -0.73885 -24.06
13 127 0.25 -0.67449 -20.06
14 128 0.27 -0.61281 -19.06
15 129 0.29 -0.55338 -18.06
16 130 0.31 -0.49585 -17.06
17 130 0.33 -0.43991 -17.06
18 135 0.35 -0.38532 -12.06
19 137 0.37 -0.33185 -10.06
20 139 0.39 -0.27932 -8.06
21 141 0.41 -0.22754 -6.06
22 143 0.43 -0.17637 -4.06
23 144 0.45 -0.12566 -3.06
24 147 0.47 -0.07527 -0.06
25 148 0.49 -0.02507 0.94
26 149 0.51 0.02507 1.94
27 149 0.53 0.07527 1.94
28 150 0.55 0.12566 2.94
29 151 0.57 0.17637 3.94
30 153 0.59 0.22754 5.94
31 154 0.61 0.27932 6.94
32 157 0.63 0.33185 9.94
33 158 0.65 0.38532 10.94
34 163 0.67 0.43991 15.94
35 165 0.69 0.49585 17.94
36 166 0.71 0.55338 18.94
37 167 0.73 0.61281 19.94
38 168 0.75 0.67449 20.94
39 171 0.77 0.73885 23.94
40 172 0.79 0.80642 24.94
41 175 0.81 0.87790 27.94
42 178 0.83 0.95417 30.94
43 183 0.85 1.03643 35.94
44 185 0.87 1.12639 37.94
45 187 0.89 1.22653 39.94
46 191 0.91 1.34076 43.94
47 197 0.93 1.47579 49.94
48 202 0.95 1.64485 54.94
49 206 0.97 1.88079 58.94
50 213 0.99 2.32635 65.94
10 116 0.19 -0.87790 -31.06
11 119 0.21 -0.80642 -28.06
12 123 0.23 -0.73885 -24.06
13 127 0.25 -0.67449 -20.06
14 128 0.27 -0.61281 -19.06
15 129 0.29 -0.55338 -18.06
16 130 0.31 -0.49585 -17.06
17 130 0.33 -0.43991 -17.06
18 135 0.35 -0.38532 -12.06
19 137 0.37 -0.33185 -10.06
20 139 0.39 -0.27932 -8.06
21 141 0.41 -0.22754 -6.06
22 143 0.43 -0.17637 -4.06
23 144 0.45 -0.12566 -3.06
24 147 0.47 -0.07527 -0.06
25 148 0.49 -0.02507 0.94
26 149 0.51 0.02507 1.94
27 149 0.53 0.07527 1.94
28 150 0.55 0.12566 2.94
29 151 0.57 0.17637 3.94
30 153 0.59 0.22754 5.94
31 154 0.61 0.27932 6.94
32 157 0.63 0.33185 9.94
33 158 0.65 0.38532 10.94
34 163 0.67 0.43991 15.94
35 165 0.69 0.49585 17.94
36 166 0.71 0.55338 18.94
37 167 0.73 0.61281 19.94
38 168 0.75 0.67449 20.94
39 171 0.77 0.73885 23.94
40 172 0.79 0.80642 24.94
41 175 0.81 0.87790 27.94
42 178 0.83 0.95417 30.94
43 183 0.85 1.03643 35.94
44 185 0.87 1.12639 37.94
45 187 0.89 1.22653 39.94
46 191 0.91 1.34076 43.94
47 197 0.93 1.47579 49.94
48 202 0.95 1.64485 54.94
49 206 0.97 1.88079 58.94
50 213 0.99 2.32635 65.94
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
-3.00000 -2.00000 -1.00000 0.00000 1.00000 2.00000 3.00000
-80
-60
-40
-20
0
20
40
60
80
Q-Q Plot of Utility Charges (Electricity Costs)
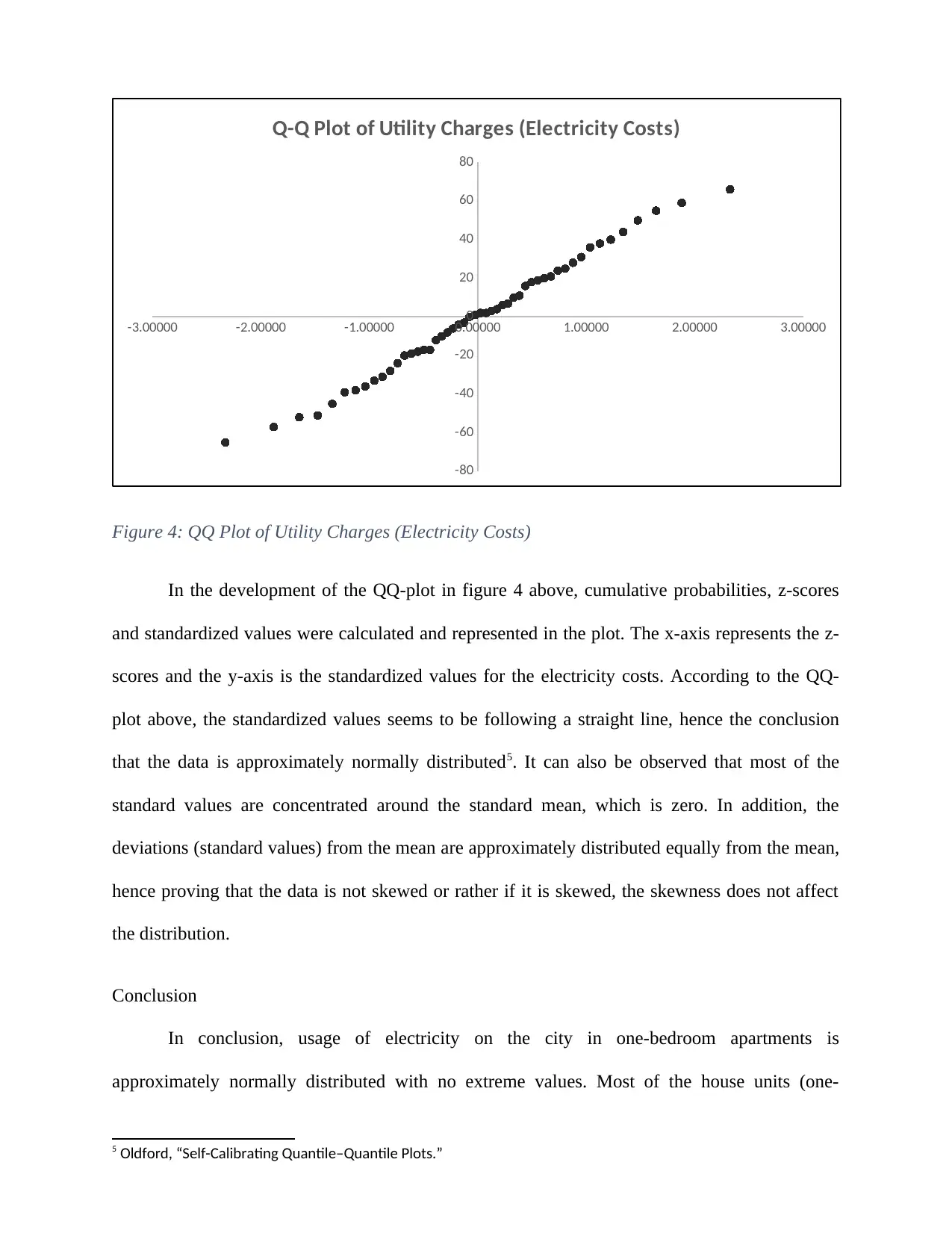
Figure 4: QQ Plot of Utility Charges (Electricity Costs)
In the development of the QQ-plot in figure 4 above, cumulative probabilities, z-scores
and standardized values were calculated and represented in the plot. The x-axis represents the z-
scores and the y-axis is the standardized values for the electricity costs. According to the QQ-
plot above, the standardized values seems to be following a straight line, hence the conclusion
that the data is approximately normally distributed5. It can also be observed that most of the
standard values are concentrated around the standard mean, which is zero. In addition, the
deviations (standard values) from the mean are approximately distributed equally from the mean,
hence proving that the data is not skewed or rather if it is skewed, the skewness does not affect
the distribution.
Conclusion
In conclusion, usage of electricity on the city in one-bedroom apartments is
approximately normally distributed with no extreme values. Most of the house units (one-
5 Oldford, “Self-Calibrating Quantile–Quantile Plots.”
-80
-60
-40
-20
0
20
40
60
80
Q-Q Plot of Utility Charges (Electricity Costs)
Figure 4: QQ Plot of Utility Charges (Electricity Costs)
In the development of the QQ-plot in figure 4 above, cumulative probabilities, z-scores
and standardized values were calculated and represented in the plot. The x-axis represents the z-
scores and the y-axis is the standardized values for the electricity costs. According to the QQ-
plot above, the standardized values seems to be following a straight line, hence the conclusion
that the data is approximately normally distributed5. It can also be observed that most of the
standard values are concentrated around the standard mean, which is zero. In addition, the
deviations (standard values) from the mean are approximately distributed equally from the mean,
hence proving that the data is not skewed or rather if it is skewed, the skewness does not affect
the distribution.
Conclusion
In conclusion, usage of electricity on the city in one-bedroom apartments is
approximately normally distributed with no extreme values. Most of the house units (one-
5 Oldford, “Self-Calibrating Quantile–Quantile Plots.”

bedroom) pay for electricity between 120 to 200 dollars. Finally, usage of electricity in the city
for one-bedroomed apartments does not differ extensively from one unit to another and the
distribution produces less extreme values (outliers) compared to the ideal standard normal. Using
standard normal tables, histogram, and boxplot, we conclude that the data is normally
distributed. Therefore, the results from these methods are homogenous.
Bibliography
Abdal-sahib, Reem, Shahah Musaed Altammar, Haffiezhah An-nadiah Azlan, Ali Aytemur,
Stephanie Balters, Martin Steinert, Christo A. Bisschoff, et al. “Testing for Normality.”
Frontiers in Psychology 98, no. 1 (2013): 1–8. https://doi.org/10.3389/fpsyg.2014.01470.
Fletcher, J. “Normal Distribution.” BMJ 338, no. feb18 2 (February 18, 2009): b646–b646.
https://doi.org/10.1136/bmj.b646.
for one-bedroomed apartments does not differ extensively from one unit to another and the
distribution produces less extreme values (outliers) compared to the ideal standard normal. Using
standard normal tables, histogram, and boxplot, we conclude that the data is normally
distributed. Therefore, the results from these methods are homogenous.
Bibliography
Abdal-sahib, Reem, Shahah Musaed Altammar, Haffiezhah An-nadiah Azlan, Ali Aytemur,
Stephanie Balters, Martin Steinert, Christo A. Bisschoff, et al. “Testing for Normality.”
Frontiers in Psychology 98, no. 1 (2013): 1–8. https://doi.org/10.3389/fpsyg.2014.01470.
Fletcher, J. “Normal Distribution.” BMJ 338, no. feb18 2 (February 18, 2009): b646–b646.
https://doi.org/10.1136/bmj.b646.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 13
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





