Business Numeracy Portfolio Assignment - Weeks 1-8 - [University Name]

This Numeracy Portfolio assignment showcases a student's understanding of fundamental mathematical and financial concepts relevant to business. The assignment covers a wide range of topics, including the laws of indices, roots, and logarithms; simple and compound interest calculations, including semi-annual and quarterly compounding; linear relationships and solving linear equations; the future value of money and net present value (NPV) calculations; and the presentation of data using histograms. The student demonstrates proficiency in applying these concepts to solve practical problems, providing detailed workings and explanations. The assignment also includes skills audits to self-assess the understanding of each concept. The student has successfully calculated the Net Present Value (NPV) of an investment project and provided reasoning for whether to proceed with the project. The student also analyzed a dataset and created a histogram to represent the data.

Student Name
Student ID
Tutor
Portfolio Contents
1

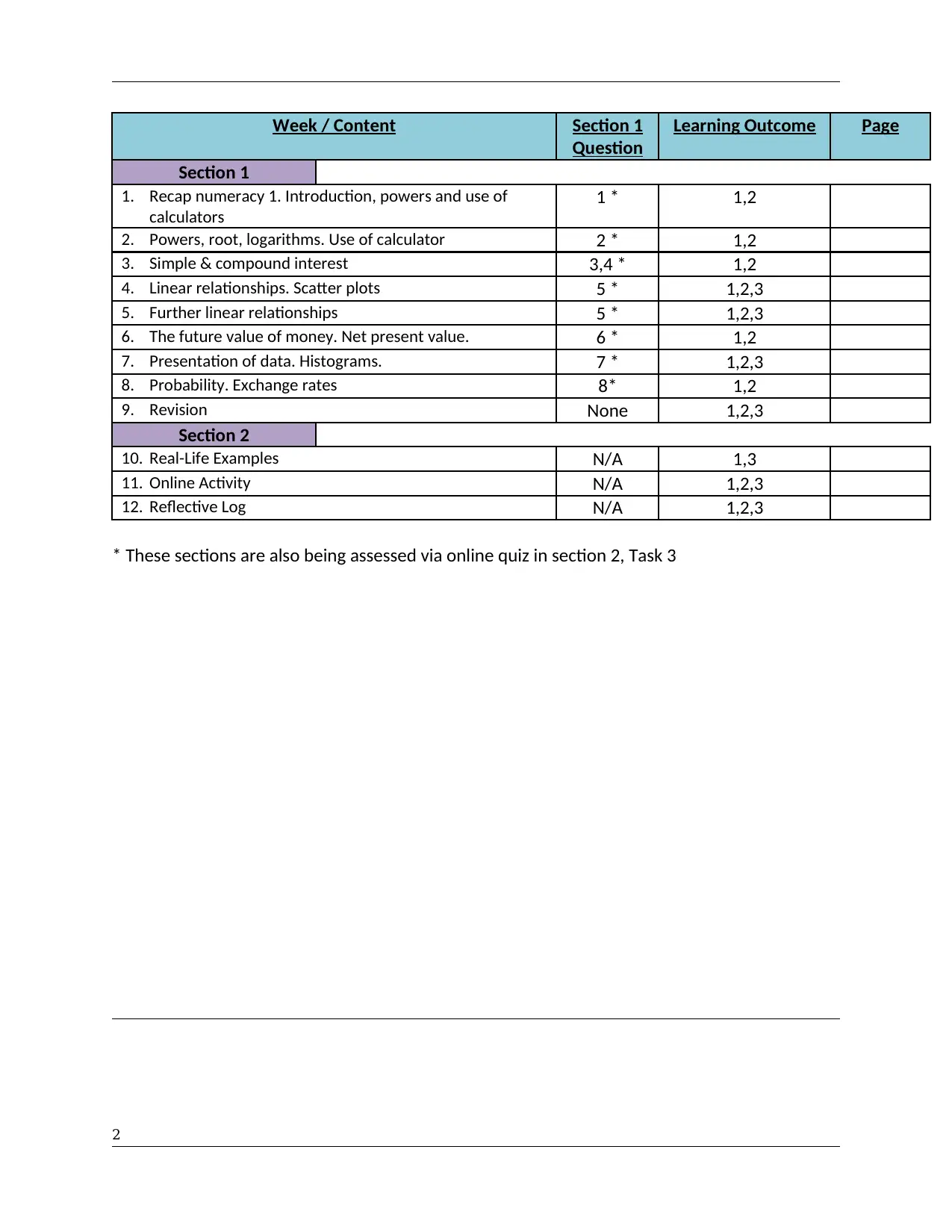
Week / Content Section 1
Question
Learning Outcome Page
Section 1
1. Recap numeracy 1. Introduction, powers and use of
calculators
1 * 1,2
2. Powers, root, logarithms. Use of calculator 2 * 1,2
3. Simple & compound interest 3,4 * 1,2
4. Linear relationships. Scatter plots 5 * 1,2,3
5. Further linear relationships 5 * 1,2,3
6. The future value of money. Net present value. 6 * 1,2
7. Presentation of data. Histograms. 7 * 1,2,3
8. Probability. Exchange rates 8* 1,2
9. Revision None 1,2,3
Section 2
10. Real-Life Examples N/A 1,3
11. Online Activity N/A 1,2,3
12. Reflective Log N/A 1,2,3
* These sections are also being assessed via online quiz in section 2, Task 3
2

Section 1
You are required to complete this section immediately after completing the class sessions
related to each question.
Answer all questions and show your workings and/or explain your results.
Marks will be awarded for good presentation.
You may use your calculator as required.
You must show your workings.
QUESTION 1 [7 marks]
Powers and Roots:
a) State three Laws of indices and provide an example of each law (5 marks)
b) Simplify (1 mark)
c) Evaluate (1 mark)
[TYPE YOUR ANSWER HERE]
a) Indices is the way of representing the large numbers into short way. Three laws which can
represent indices in the better way are
Law 1: a^m * a^n = a^(m+n)
This is the first law which shows that when multiplying two identical numbers with
similar power, the final result will be same to the power of both exponents when they are
added together.
Example: 2^2 * 2^3 = 2^5
Law 2: a^m / a^n = a^(m-n)
Second law tells that when we divide two same numbers having different power, then
the power will be subtracted.
Example: 3^4 / 3^2 = 3^2
Law 3: (a^m)^n = a^(m*n)
The last and third law tells that if any number is having the power and that power is also
having the power, then to get the final result we have to multiply both the powers.
Example: (4^2)^3 = 4^6
b) 10^3 * 10^2
= (10)^5 = 100000
c) (5^3)^4 = 5^12 = 244140625
3

4

QUESTION 2 [7 marks]
a) Finding a root is the inverse of raising a number to a power
List three examples of root laws and explain what they are (5 marks)
b) Evaluate (1 mark)
c) Scientific notation is a special way to express very large or very small numbers and make
them easy to handle. Express 680,000 in a scientific notation (1 mark)
a) Square root is the function which takes any positive number as an input and return the
positive number in output, which would have been doubled or squared. The square root of any
number say x is denoted by
√ x
Example 1: if x ≥ 0 and y ≥ 0, the equation is
√ (x*y) = √a * √b
This only works in the multiplying factors.
Example 2: √ x^2 = I x I
√ (-2)^2 = I -2 I = 2
The square root will always give the positive number.
Example 3: if a ≥ 0, then √a^2 = a
√ 5^2 = 5
b) (1,000,000)^(1/6) = 10
c) scientific notation of 680,000 is = 6.8 * 10^5
[TYPE YOUR ANSWER TO QUESTION 2 HERE]
5

SKILLS AUDIT: WEEKS 1 – 2
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t do
1. I understand what a power of a number is ☐ ☐ ☐ ☐
2. I can perform calculations and
simplifications using indices
☐ ☐ ☐ ☐
3. I understand what a root of a number is ☐ ☐ ☐ ☐
4. I can perform calculations and
simplifications using roots, using a scientific
or financial calculator when required
☐ ☐ ☐ ☐
QUESTION 3 [10 marks]
Nelofa invests £50,000 at an interest rate of 3% per annum.
Calculate the final balance after 5 years:
a) Using the simple interest? (1 mark)
b) Using the interest compounded annually? (3 marks)
c) Using the interest compounded semi-annually? (3 marks)
d) Using the interest compounded quarterly? (3 marks)
[TYPE YOUR ANSWER TO QUESTION 3 HERE]
a) SI= P*R*T/100
where P = total amount occurred
A = capital amount
r = interest rate
t =given time period
therefore, A = 50,000*3*5/100
A = £7500
6

b) Compound interest annually = A = P[(1+r) n-1]
P =principle amount
r = rate of interest
t = total number of years
n = number of time interest is compound
= 50000 [(1+0.03)5-1]
= 50000*0.1592
= £7960
c) Compound interest semi-annually= P[(1+r/2) 2*n-1]
here, n=2
Therefore A = 50,000 [(1+0.03/2) 2*5-1]
= £8025
d) compound interest quarterly, then n = 4
therefore, A = 50,000 [(1+0.03/4) 4*5-1]
= £8060
7

QUESTION 4 [7 marks]
a) Jojoba invests £80,000 at a 4.5% interest rate annually.
Compounding the interest annually, how long will it take his investment
to double? (3
marks)
b) Roger deposits £8,000 in a bank savings account and after 10 years his balance is
£9751.96
Calculate the compound interest he received? Give your answer in three
significant figures. (4 marks)
[TYPE YOUR ANSWER TO QUESTION 4 HERE]
a) P0 = £80,000, r = 4.5%
Lets take P0 = initial investment
P = the amount after time t
r = interest rate
t = time
lets take x = initial investment (P0)
2x = final amount (P)= 1, 60, 000
C= P[(1+r)n]
160000= 80000 (1+0.04.5)n
= 15.8 years
It is therefore calculating the same by considering the rule of 72, it is expected to double in 16
years and will stand to 72/4.5
b) P0 = £8000
P = 9751.96
t = 10 years
We have to calculate interest rate first on the basis of given figures
P = P0(1+rt)
9751.96 = 8000(1+r*10)
9751.96/8000 = 1+10r
0.21 = 10r
r = 0.021
r = 2%
I) The compound interest received by roger annually i.e. n=1
A = p(1+r/n)^(rt)
A = 8000(1+0.021)^(10)
A = 8000(1.021)^10

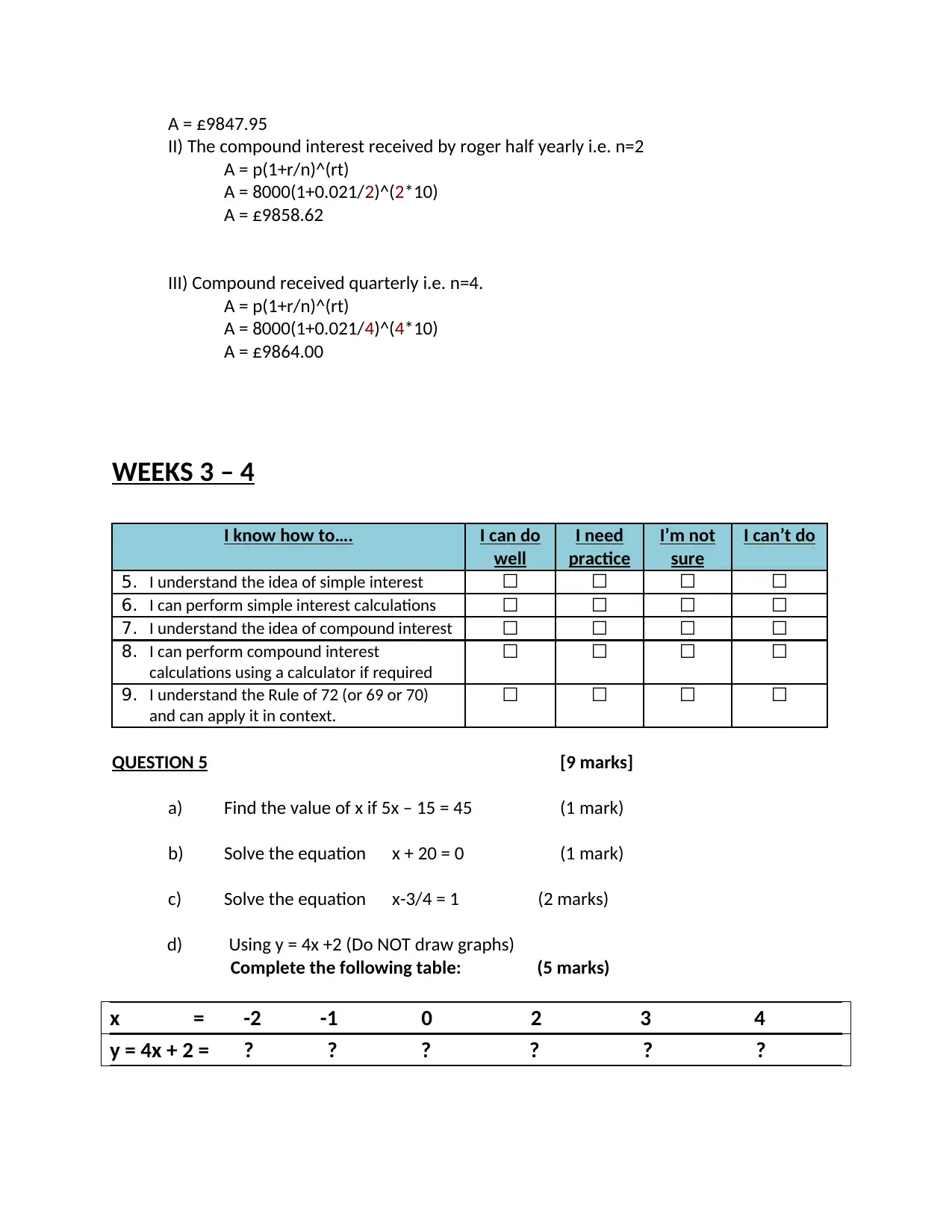
A = £9847.95
II) The compound interest received by roger half yearly i.e. n=2
A = p(1+r/n)^(rt)
A = 8000(1+0.021/2)^(2*10)
A = £9858.62
III) Compound received quarterly i.e. n=4.
A = p(1+r/n)^(rt)
A = 8000(1+0.021/4)^(4*10)
A = £9864.00
WEEKS 3 – 4
I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t do
5. I understand the idea of simple interest ☐ ☐ ☐ ☐
6. I can perform simple interest calculations ☐ ☐ ☐ ☐
7. I understand the idea of compound interest ☐ ☐ ☐ ☐
8. I can perform compound interest
calculations using a calculator if required
☐ ☐ ☐ ☐
9. I understand the Rule of 72 (or 69 or 70)
and can apply it in context.
☐ ☐ ☐ ☐
QUESTION 5 [9 marks]
a) Find the value of x if 5x – 15 = 45 (1 mark)
b) Solve the equation x + 20 = 0 (1 mark)
c) Solve the equation x-3/4 = 1 (2 marks)
d) Using y = 4x +2 (Do NOT draw graphs)
Complete the following table: (5 marks)
x = -2 -1 0 2 3 4
y = 4x + 2 = ? ? ? ? ? ?

[TYPE YOUR ANSWER TO QUESTION 5 HERE]
a) 5x – 15 = 45
5x = 45+15
x = 60/5
x = 12
b) if x+20 = 0, then
X = -20
c) x-3/4 = 1
x = 4+3
x = 7
d) y = 4x + 2
values of x = -2 -1 0 2 3 4
values of y = 4*-2 + 2 (4*-1+2) 4*0+2 4*2+2 4*3+2 4*4+2
values of x= -2 -1 0 2 3 4
values of y = -6 -2 2 10 14 18
WEEK 5

I know how to…. I can do
well
I need
practice
I’m not
sure
I can’t do
10.I understand linear relationship between
two variables
☐ ☐ ☐ ☐
11.I can work out linear equation problems
given in this session
☐ ☐ ☐ ☐
12.I can plot a scatter graph from a set of data ☐ ☐ ☐ ☐
13.I understand the y-intercept and slope
(gradient) of a line graph and interpret their
meaning in real situations ().
☐ ☐ ☐ ☐
14.I can use scatter plot to derive a linear
relationship between two variables ().
☐ ☐ ☐ ☐
15.I am able to explain the use of scatter
graphs in business context
☐ ☐ ☐ ☐

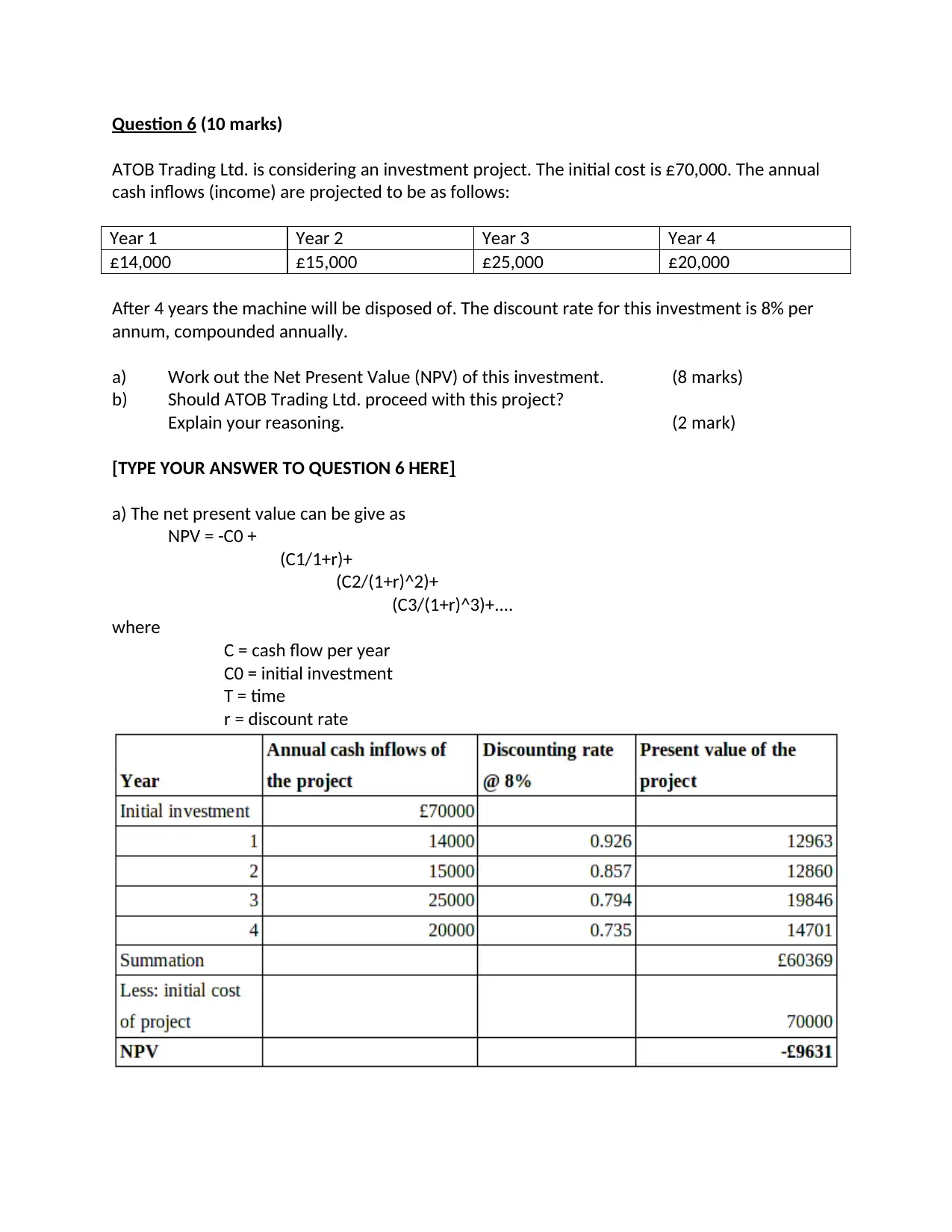
Question 6 (10 marks)
ATOB Trading Ltd. is considering an investment project. The initial cost is £70,000. The annual
cash inflows (income) are projected to be as follows:
Year 1 Year 2 Year 3 Year 4
£14,000 £15,000 £25,000 £20,000
After 4 years the machine will be disposed of. The discount rate for this investment is 8% per
annum, compounded annually.
a) Work out the Net Present Value (NPV) of this investment. (8 marks)
b) Should ATOB Trading Ltd. proceed with this project?
Explain your reasoning. (2 mark)
[TYPE YOUR ANSWER TO QUESTION 6 HERE]
a) The net present value can be give as
NPV = -C0 +
(C1/1+r)+
(C2/(1+r)^2)+
(C3/(1+r)^3)+....
where
C = cash flow per year
C0 = initial investment
T = time
r = discount rate