Statistics for Business: Analysis of Data and Probability
VerifiedAdded on 2020/03/16
|12
|877
|39
Homework Assignment
AI Summary
This document presents a comprehensive solution to a statistics assignment, focusing on business applications. It begins by classifying data types and measurement levels for various variables like gender, GPA, and number of children. The assignment then delves into calculating measures of central tendency (mean, median, mode) and standard deviation, along with identifying unusual observations and outliers. The solution includes the analysis of quiz scores, determining skewness and average performance. Furthermore, it addresses probability calculations related to a scenario involving alternator failures. Finally, the assignment concludes with constructing a 95% confidence interval and determining the required sample size, utilizing the t-distribution due to a sample size less than 30. A line chart illustrating the trend of data is also provided, demonstrating the decrease in the number of steps over time.

STATISTICS FOR BUSINESS
Assignment
STUDENT ID
[Pick the date]
Assignment
STUDENT ID
[Pick the date]
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 1
1. Gender
Data type: Categorical
Measurement level: Nominal
This is because gender type male and female is measured at nominal scale.
2. Approximate undergraduate college GPA
Data type: Continuous
Measurement level: Ratio
This is because undergraduate college GPA such as 1.0 to 4.0 would be a mathematical operation
and hence, ratio is the measurement level.
3. Number of hours per week
Data type: Continuous
Measurement level: Ratio
This is because number of hours per week would be a mathematical operation and hence, ratio is
the measurement level.
4. Ideal number of children for a married couple
Data type: Discrete
Measurement level: Ratio
1. Gender
Data type: Categorical
Measurement level: Nominal
This is because gender type male and female is measured at nominal scale.
2. Approximate undergraduate college GPA
Data type: Continuous
Measurement level: Ratio
This is because undergraduate college GPA such as 1.0 to 4.0 would be a mathematical operation
and hence, ratio is the measurement level.
3. Number of hours per week
Data type: Continuous
Measurement level: Ratio
This is because number of hours per week would be a mathematical operation and hence, ratio is
the measurement level.
4. Ideal number of children for a married couple
Data type: Discrete
Measurement level: Ratio

This is because number of children would be a mathematical operation and hence, ratio is the
measurement level.
5. Describe parents
Data type: Categorical
Measurement level: Ordinal
This is because the given statistics shows the order 1 for the respective month which dominate up
to order 5 for father and hence, the ordinal is the measurement level.
Question 2
Given data
(a) Computation of mean, median and mode
These values have been computed with the help of excel functions i.e.
Mean = AVERAGE ()
Median = MEDIAN ()
measurement level.
5. Describe parents
Data type: Categorical
Measurement level: Ordinal
This is because the given statistics shows the order 1 for the respective month which dominate up
to order 5 for father and hence, the ordinal is the measurement level.
Question 2
Given data
(a) Computation of mean, median and mode
These values have been computed with the help of excel functions i.e.
Mean = AVERAGE ()
Median = MEDIAN ()
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Mode = MODE ()
(b) It can be seen that measures of central tendency i.e. mean, median and mode are not
equal and hence, the measure of central tendency is not agreed.
Mean ≠ Median≠ Mode
(c) Standard deviation
This has been computed with the help of excel functions STDEV ().
(d) Sort and standardized the data
x=724.67
s=114.28
For each of the given value, it is essential to find the standardized score as highlighted below:
zi= ( xi−x
s )
(b) It can be seen that measures of central tendency i.e. mean, median and mode are not
equal and hence, the measure of central tendency is not agreed.
Mean ≠ Median≠ Mode
(c) Standard deviation
This has been computed with the help of excel functions STDEV ().
(d) Sort and standardized the data
x=724.67
s=114.28
For each of the given value, it is essential to find the standardized score as highlighted below:
zi= ( xi−x
s )
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

(e) Empirical rule suggests that unusual observation are those which are beyond x ± 2 s and
the outliers are those which are beyond x ± 3 s .
Unusual observations:
x ± 2 s=724.67 ± ( 2∗114.3 ) =496.1 , 953.3
the outliers are those which are beyond x ± 3 s .
Unusual observations:
x ± 2 s=724.67 ± ( 2∗114.3 ) =496.1 , 953.3

The observation 1030 fall outsides the range (496.1953.3)and hence, it is termed as unusual
observation.
Outliers:
x ± 3 s=724.67 ± ( 3∗114.3 )=381.8 1067.6
There are no outliers present because based on empirical rule none of the value lies outside the
above highlighted range.
(f) Based on the three sigma empirical rule, it can be said that the data is from normal
population because nearly 99.7% of the data is fall within the range of three standard
deviation of the mean.
x ± 3 s=724.67 ± ( 3∗114.3 )=381.8 1067.6 (All values fall under this range)
Question 3
(a) Computation of mean, median and mode
For quiz 1
Quiz 1: 60, 60, 60, 60, 71, 73, 74, 75, 88, 99.
Mean= 60+60+60+60+71+73+74 +75+88+ 99
10 =720
10 =72
Median= ( 71+73 )
2 =72
Mode=60
For quiz 2
observation.
Outliers:
x ± 3 s=724.67 ± ( 3∗114.3 )=381.8 1067.6
There are no outliers present because based on empirical rule none of the value lies outside the
above highlighted range.
(f) Based on the three sigma empirical rule, it can be said that the data is from normal
population because nearly 99.7% of the data is fall within the range of three standard
deviation of the mean.
x ± 3 s=724.67 ± ( 3∗114.3 )=381.8 1067.6 (All values fall under this range)
Question 3
(a) Computation of mean, median and mode
For quiz 1
Quiz 1: 60, 60, 60, 60, 71, 73, 74, 75, 88, 99.
Mean= 60+60+60+60+71+73+74 +75+88+ 99
10 =720
10 =72
Median= ( 71+73 )
2 =72
Mode=60
For quiz 2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Quiz 2: 65, 65, 65, 65, 70, 74, 79, 79, 79, 79
Mean= 65+65+65+65+70+ 74+79+79+79+79
10 = 720
10 =72
Median= ( 70+74 )
2 =72
Mode=65∧79
For quiz 3
Quiz 3: 66, 67, 70, 71, 72, 72, 74, 74, 95, 99
Mean= 66+67+70+71+72+72+74+ 74+95+ 99
10 =760
10 =76
Median= ( 72+72 )
2 =72
Mode=72∧74
For quiz 4
Quiz 4: 10, 49, 70, 80, 85, 88, 90, 93, 97, 98
Mean=10+ 49+70+80+ 85+88+ 90+93+97+98
10 = 760
10 =76
Median= ( 85+88 )
2 =86.50
Mode=¿ There is no mode for the data of quiz 4.
Mean= 65+65+65+65+70+ 74+79+79+79+79
10 = 720
10 =72
Median= ( 70+74 )
2 =72
Mode=65∧79
For quiz 3
Quiz 3: 66, 67, 70, 71, 72, 72, 74, 74, 95, 99
Mean= 66+67+70+71+72+72+74+ 74+95+ 99
10 =760
10 =76
Median= ( 72+72 )
2 =72
Mode=72∧74
For quiz 4
Quiz 4: 10, 49, 70, 80, 85, 88, 90, 93, 97, 98
Mean=10+ 49+70+80+ 85+88+ 90+93+97+98
10 = 760
10 =76
Median= ( 85+88 )
2 =86.50
Mode=¿ There is no mode for the data of quiz 4.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

(b) It is apparent that measures of central tendency i.e. mean, median and mode are not same
and hence, the measures of central tendency are not agreed.
(c) The value of mean, median has been computed for all the quizzes. However, quiz four
does not have mode.
(d) For quiz 1 – Data is skewed and direction is towards the left.
For quiz 2 – Data is roughly symmetric.
For quiz 3 – Data is skewed and direction is towards the right.
For quiz 4 – Data is skewed and direction is towards the left.
(e) For quiz 1 – The avg. performance is 72.
For quiz 2 - The avg. performance is 72.
For quiz 3 - The avg. performance is 76.
For quiz 4 - The avg. performance is 76.
The average performance of students in quiz 1 and quiz 2 are lower than the performance in quiz
3 and 4.
Question 4
Probability that in a given alternator will fail on a one hour flight = 0.02
(a) Probability that both will fail
P ( bothwill fail )=¿
and hence, the measures of central tendency are not agreed.
(c) The value of mean, median has been computed for all the quizzes. However, quiz four
does not have mode.
(d) For quiz 1 – Data is skewed and direction is towards the left.
For quiz 2 – Data is roughly symmetric.
For quiz 3 – Data is skewed and direction is towards the right.
For quiz 4 – Data is skewed and direction is towards the left.
(e) For quiz 1 – The avg. performance is 72.
For quiz 2 - The avg. performance is 72.
For quiz 3 - The avg. performance is 76.
For quiz 4 - The avg. performance is 76.
The average performance of students in quiz 1 and quiz 2 are lower than the performance in quiz
3 and 4.
Question 4
Probability that in a given alternator will fail on a one hour flight = 0.02
(a) Probability that both will fail
P ( bothwill fail )=¿

P ( bothwill fail )=0.0004
(b) Probability that neither will fail
P ( neither will fail ) =¿
P ( neither will fail ) =(0.982)
P ( neither will fail ) =0.9604
(c) Probability that one or the other will fail
P ( one∨the other will fail ) =1− { P ( neither will fail ) }
¿ 1−(0.9604)
¿ 0.0396
Question 5
Given data
(b) Probability that neither will fail
P ( neither will fail ) =¿
P ( neither will fail ) =(0.982)
P ( neither will fail ) =0.9604
(c) Probability that one or the other will fail
P ( one∨the other will fail ) =1− { P ( neither will fail ) }
¿ 1−(0.9604)
¿ 0.0396
Question 5
Given data
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

(a) 95% confidence interval
Mean = 3,279
Standard deviation = 97.05
Sample size = 18
As per central limit theorem, the sample size is lower than 30 and hence, t value would be used.
Degree of freedom = Sample size -1 = 18-1 = 17
The value of t stat for 95% confidence interval and 17 degree of freedom = 2.1098
Now,
95 % confidence interval=Mean ±t stat ¿
Upper limit of 95% confidence interval = 3279+2.1098 ( 97.05
√18 )=3326.98
Mean = 3,279
Standard deviation = 97.05
Sample size = 18
As per central limit theorem, the sample size is lower than 30 and hence, t value would be used.
Degree of freedom = Sample size -1 = 18-1 = 17
The value of t stat for 95% confidence interval and 17 degree of freedom = 2.1098
Now,
95 % confidence interval=Mean ±t stat ¿
Upper limit of 95% confidence interval = 3279+2.1098 ( 97.05
√18 )=3326.98
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Lower limit of 95% confidence interval = 3279−2.1098 ( 97.05
√18 )=3230.45
95% confidence interval [3230.45 3326.98]
(b) Sample size =?
In order to obtained an error of ± 20 steps with the 95% confidence.
Now,
Margin of error E=t stat ¿
20=2.1098 ¿
√ Sample ¿ ¿ 204.75
20 ¿
Sample ¿ ¿
Sample ¿ 104.81 105
Therefore, the requisite sample size is 105.
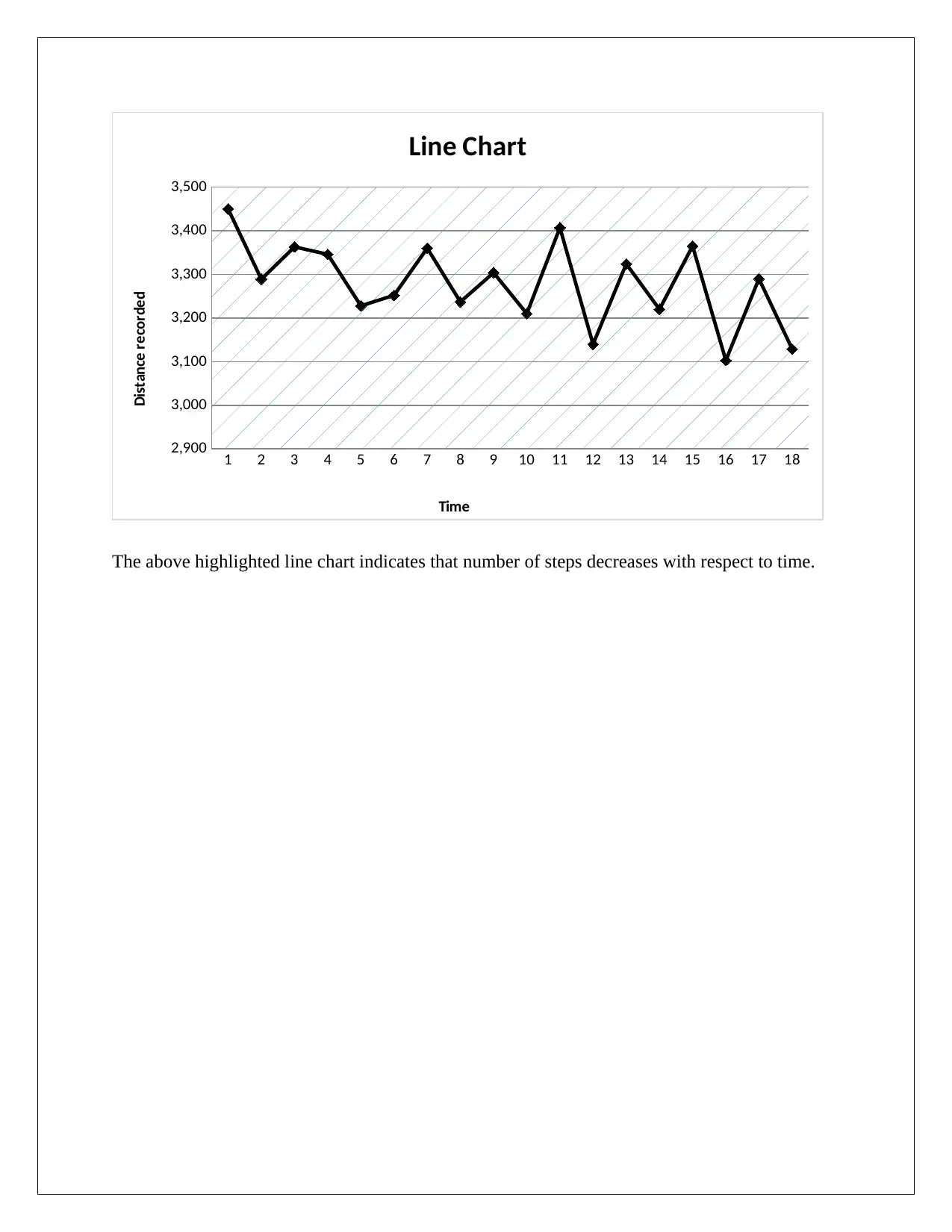
(c) Line chart of the data set
√18 )=3230.45
95% confidence interval [3230.45 3326.98]
(b) Sample size =?
In order to obtained an error of ± 20 steps with the 95% confidence.
Now,
Margin of error E=t stat ¿
20=2.1098 ¿
√ Sample ¿ ¿ 204.75
20 ¿
Sample ¿ ¿
Sample ¿ 104.81 105
Therefore, the requisite sample size is 105.
(c) Line chart of the data set
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2,900
3,000
3,100
3,200
3,300
3,400
3,500
Line Chart
Time
Distance recorded
The above highlighted line chart indicates that number of steps decreases with respect to time.
2,900
3,000
3,100
3,200
3,300
3,400
3,500
Line Chart
Time
Distance recorded
The above highlighted line chart indicates that number of steps decreases with respect to time.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




