University Mini-Project MCE226L: Mittag-Leffler Function in C

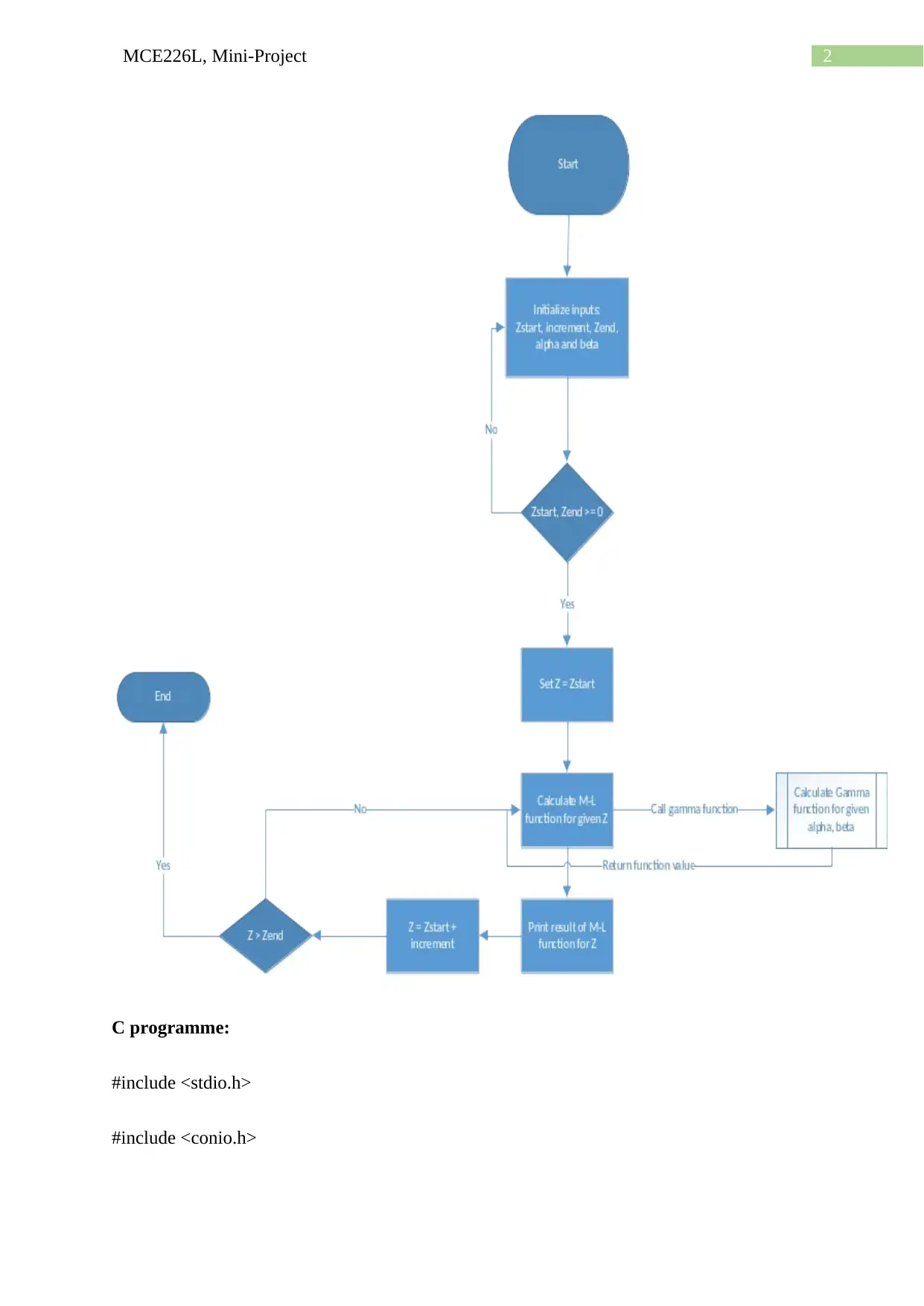
This mini-project, designed for MCE226L, focuses on the Mittag-Leffler function, a special function used in various engineering applications. The project involves developing a C program to calculate the Mittag-Leffler function for a user-defined range of input values. The program utilizes the Gamma function and approximates the infinite sum of the Mittag-Leffler function by iterating until the difference between successive terms is less than a specified tolerance. The code prompts the user to input the starting and ending values of the range, increment, and the parameters alpha and beta. The program then calculates and prints the values of the Mittag-Leffler function for each value within the specified range, providing a practical application of numerical methods and programming skills. The solution includes the C program code, a flowchart of the algorithm, and a sample output demonstrating the program's functionality.

Running head: MCE226L, Mini-Project
Type equation here .
MCE226L, Mini-Project
Name of the Student
Name of the University
Author Note

1MCE226L, Mini-Project
The Mittag-Leffler function with parameters α, β are given by the following expression.
M L ( α , β ) ( z )=∑
k=0
∞ zk
Γ ( α∗k+ β )
The Γ symbol is the gamma function which is defined by,
Γ ( n)=(n−1)!
The infinite sum of M-L function is approximated by certain number of terms in which the
error between current and next iteration is less than the tolerance which is En =0.0001. The
values of α, β are considered positive integers here. The values of M-L function for different
z in a user-defined range are printed using C programming.
Flowchart of algorithm:

2MCE226L, Mini-Project
C programme:
#include <stdio.h>
#include <conio.h>

3MCE226L, Mini-Project
#include <math.h>
#include <stdlib.h>
int gammafunc(int num);
int main()
{
// initialization of paramters
float zstart;
float zend;
float inc;
float z;
int alpha;
int beta;
printf("Enter positive value of starting z: ");
scanf("%f",&zstart);
while (zstart<0)
{

4MCE226L, Mini-Project
printf("You must enter positive value of starting z: ");
scanf("%f",&zstart);
}
printf("Enter positive value of ending z: ");
scanf("%f",&zend);
while (zend<0)
{
printf("You must enter positive value of ending z: ");
scanf("%f",&zend);
}
printf("Enter positive value of increment: ");
scanf("%f",&inc);
printf("Enter value of alpha which is integer: ");
scanf("%d",&alpha);
printf("Enter value of beta which is integer: ");
scanf("%d",&beta);

5MCE226L, Mini-Project
for (z=zstart;z<zend;z=z+inc)
{
float out1; int k;float out2; k=0;
out1= 0;
out2 = pow(z,k)/gammafunc(alpha*(k) + beta);
// Calculation loop
while (fabs(out2 - out1)>=0.0001) // tolerance is 1e-4
{
out1 = out1 + pow(z,k)/gammafunc(alpha*k + beta);
out2 = out1 + pow(z,k+1)/gammafunc(alpha*(k+1) + beta);
k=k+1;
}
printf("The value of the Mittag-Leffler function for the input %.4f is %.4f \n",z,out2);
}
return 0;
}
int gammafunc(int num) // function definition
{

6MCE226L, Mini-Project
{
int fact=1,i;
for (i=1;i<=num-1;i++)
{
fact = fact*i;
}
return fact;
} // return statement
}
Sample Output:

7MCE226L, Mini-Project