University of South Africa MAT1512 Calculus A: Tutorial Letter 001

This document is Tutorial Letter 001 for the MAT1512 Calculus A module at the University of South Africa (Unisa). It serves as an introductory guide for students enrolled in the year module, providing essential information about the course. The letter details the module's purpose, which is to equip students with fundamental skills in differential and integral calculus, essential for various scientific and economic fields. It outlines specific learning outcomes covering limits, differentiation, integration, and their applications, along with assessment criteria. The tutorial letter also includes lecturer contact information, resources such as the prescribed and recommended textbooks, and guidelines for online study via myUnisa. Furthermore, it presents the assessment plan, detailing the year mark and final examination components. In essence, this tutorial letter acts as a roadmap for students, ensuring they are well-informed about the module's structure, expectations, and available support systems to facilitate their success in Calculus A.

MAT1512/001/0/2021
of south africa
Tutorial Letter 001/0/2021
CALCULUS A
MAT1512
Year module
Department of Mathematical Sciences
IMPORTANT INFORMATION:
This tutorial letter contains important information about your module.
Please activate your myUNISA and myLife e-mail account(s) and make sure that you have regular
access to the myUNISA module website MAT1512-21-Y1, as well as your group site.
Note: This is a fully online module. It is therefore, only available on myUnisa.
BAR CODE
Define tomorrow. university
Open Rubric

CONTENTS
Page
1 INTRODUCTION.................................................................................................................. 3
1.1 Getting started……………… .............................................................................................. 3
2 OVERVIEW of MAT1512...................................................................................................... 3
2.1 Purpose…............................................................................................................................ 5
2.2 Outcomes………………………………………………………………………………………….. 5
3 LECTURER(S) AND CONTACT DETAILS.......................................................................... 8
3.1 Lecturer(s)............................................................................................................................ 8
3.2 Department........................................................................................................................... 9
3.3 University.............................................................................................................................. 9
4 RESOURCES....................................................................................................................... 9
4.1 Joining myUNISA .................................................................................................................. 9
4.2 Prescribed book(s)…... ......................................................................................................... 10
4.3 Recommended book(s)…………......................................................................................... 10
4.4 Electronic reserves (e-reserves).......................................................................................... 10
4.5 Library services and resources………………………………………………………………… 10
5 STUDENT SUPPORT SERVICES..................................................................................... 11
6 HOW TO STUDY ONLINE ?............................................................................................. 12
6.1 What does it mean to study fully online?.......................................................................... 12
6.2 myUNISA tools…………………………………………………………………………………. 13
7 ASSESSMENT …………………………………………………………………………………. 14
7.1 Assessment plan………………………………………………………………………………… 14
7.2 Year mark and final examination/other options………………………………………………. 16
8 CONCLUSION…………………………………………………………………………………… 17
APPENDIX: GLOSSARY OF TERMS………………………………………………………… 17

MAT1512/001/0/2021
1 INTRODUCTION
Dear Student
Welcome to the MAT1512 module. We trust that you will find the mathematics studied in this module
interesting and useful, and that you will enjoy doing it.
This tutorial letter contains important information about the scheme of work, resources and
assignments for this module as well as exam admission. We urge you to read it carefully before
working through the study material, preparing the assignment(s), preparing for the examination
and addressing questions to your lecturers.
In this tutorial letter, you will find the assignments as well as instructions on the preparation and
submission of the assignments. This tutorial letter also provides all the information you need with
regard to the prescribed study material and other resources. Please study this information
carefully and make sure that you obtain the prescribed material as soon as possible.
You will access all files online, a number of tutorial letters for example, solutions to assignments,
during the semester/ year. These tutorial letters will be uploaded on myUnisa, under Additional
Re-sources and Lessons tools on myUnisa platform. A tutorial letter is our way of communicating
with you about teaching, learning and assessment.
Right from the start we would like to point out that you must read all the tutorial letters you access
from the module site immediately and carefully, as they always contain important and, sometimes
urgent information.
Because this is a fully online module, you will need to use myUnisa to study and complete the
learning activities for this course. Please visit the website for MAT1512 on myUnisa frequently.
The website for your module is MAT1512-21-Y1.
1.1 Getting started
Owing to the nature of this module, you can read about the module and find your study material
online. Go to the website at https://my.unisa.ac.za and log in using your student number and
password. Click on “myModules” at the top of the webpage and then on “Sites” in the top right
corner. In the new window, click on the grey Star icon next to the modules you want displayed on
your navigator bar. Close the window in the right corner. The select the option “Reload to see
your updated favorite sites”. Now go to your navigation bar and click on the module you want to
open.
We wish you every success with your studies!
2 OVERVIEW of MAT1512
2.1 Purpose
This module will be able useful to students interested in developing the basic skills in Calculus
which can be applied in the natural sciences and social sciences. Students who have completed
this module successfully will have an understanding of the basic ideas of Calculus.

MAT1512/001
5
2 PURPOSE AND OUTCOMES
2.1 Purpose
This module is useful to students interested in developing the basic skills in differential and integral
calculus. Differential and integral calculus are essential for physical, life and economic sciences.
Students credited with this module will have a firm understanding of the limit, continuity at a point,
differentiation and integration, together with a background in the basic techniques and some appli-
cations of Calculus.
2.1.1 Learning Assumptions: The learning is based on the assumption that students are
already competent in terms of the following outcomes or areas of learning and must:
– Have a Senior Certificate or equivalent qualification (as required) for further study.
– Have obtained an NQF/HEQF Level equivalent to 4 with the ability to:
– Be able to learn from predominantly written material in the language of tuition
– Take responsibility for their own progress and independently adjust to the learning
environment
– Have basic computer skills like using a mouse, keyboard and windows features
– Demonstrate an understanding of the most current topics in mathematics including
∗ Functions
∗ The ability to algebraically manipulate real numbers and solve equations.
∗ An ability to sketch graphs and find equations from these graphs.
∗ Substantive knowledge about basic trigonometry
∗ Knowledge about the following mathematical concepts: absolute values, partial
fractions and inequalities.
Recognition of prior learning will take place in accordance with the institution’s policy
and guidelines. Recognition takes place, where prior learning corresponds to the re-
quired NQF-HEQF level and in terms of applied competencies relevant to the content
and outcomes of the qualification, at the discretion of the department.
2.1.2 Range statement for the module: The techniques selected involve polynomial, ratio-
nal, trigonometric, exponential and logarithmic functions and their composites. This
introductory calculus module covers differentiation and integration of functions of one
variable, with applications.
2.2 Outcomes
2.2.1 Specific outcome 1:
Demonstrate knowledge of the concept of a limit of a function and its application.
Range:
The knowledge includes limits of one variable and an introduction to limits of two or more
variables.

6
Assessment criteria
– A formal definition of the limit with the correct mathematical notation is given which
embraces an understanding of the limit as the y-value of a function.
– A distinction between the limits of a function as x approaches {limx →a f (x ) } and
the value of the function at x = a is made correctly.
– Laws governing limits are stated and used to determine and evaluate limits of sums,
products, quotients and composition of functions.
– The limits of functions are evaluated graphically and numerically.
– The limit definition of continuity is used to determine whether a function is continuous
or discontinuous at a point.
– The Squeeze Theorem is used to determine certain undefined limits.
2.2.2 Specific outcome 2:
Demonstrate an understanding of differentiation.
Assessment criteria
– The derivative is defined as an instantaneous rate of change of a function.
– The first principle of differentiation is presented using different expressions.
Range: These different expressions include:
     
h
xfhxf
xf h

  0
lim ;      
x
xfxxf
xf x 

  0
lim
  x
y
xf x 

  0
lim ;      
ax
afxf
af ax 

 
lim
– Alternate derivative notations are given. Range: These include:
   xf
dx
d
dx
df
dx
dy
yxf 
– A distinction between continuity and differentiability of a function at point is made
correctly.
– A representation of the first derivative as the slope of the tangent line at the point of
tangency is given.
2.2.3 Specific outcome 3:
– Calculate derivatives.
Assessment criteria
– The derivative of a function is computed from the first principle of differentiation.
– The basic rules of differentiation such as the power rule, product and quotient rules
are used to compute derivatives of different functions.
– Range: The functions are in the form:      ][ xgxfxh  ;       xgxfxh .
   
 




  xg
xf
xh .The chain rule is used, together with other rules of differentiation to find
derivatives of composite functions.

MAT1512/001
7
2.2.4 Specific outcome 4:
– Use derivatives to solve applied problems.
Assessment criteria
– For the problem solving, the differentiation technique chosen is appropriate to the
problem.
– Mathematical notations and language are used appropriately.
– The derivative is used to find equations of tangent and normal lines of different
curves.
– Where appropriate, the Mean Value Theorem is applied.
2.2.5 Specific outcome 5:
– Demonstrate understanding of basic integration and the Fundamental Theo-
rem of Calculus
Assessment criteria
– The definite integral is defined and interpreted using:
∗ the concept of definite integral to obtain areas under the curve.
∗ as the net change in a quantity from x = a to x = b if f (x ) is the rate of change of
the quantity with respect to x .
– A function F is defined as an anti-derivative (indefinite integral) of the function f if
the derivative fF  .Anti-differentiation (integration) is recognised as the inverse
of the differentiation process.
_ The Fundamental Theorem of Calculus for a function f on an interval  ba, as:
     aFbFdxxf
b
a
 where  xF is such that    xfxF 
is reproduced and used to:-
∗ explain the way in which differentiation and integration are related.
∗ evaluate given integrals.
– Integral notation is used appropriately.
2.2.6 Specific outcome 6:
– Use integrals of simple functions to solve applied problems
Range: Simple integrals are applied but not limited to problems involving the length
of a curve, area between curves, velocity and acceleration.
Assessment criteria
– Substitution or term by term integration techniques are used appropriately.
– The anti-derivatives of basic algebraic and trigonometric functions are determined
correctly.
– For the problem solving process:-
∗ The estimations of the definite integrals of the functions are correct.
∗ The solution is consistent with the problem.
2.2.7 Specific outcome 7
– Analyse logarithmic and exponential functions.

8
Assessment criteria
– The graphs of the functions y = ex and y = ln x are reproduced.
– The relationship between ex and ln x as inversedifferentiable functions is recognised
and used as a device for simplifying calculations.
– Rules of differentiation and integration are applied to functions involving logarithmic
and exponential functions.
– Logarithmic differentiation is used correctly.
– Exponentials and logarithmic models for solving applied problems are identified.
2.2.8 Specific outcome 8
– Solve exponential growth and decay problems using elementary differential equa-
tions.
Range: The solutions are limited to first-order, separable, constant coefficient initial-
value problems, with contextual situations involving exponential growth and decay.
Assessment criteria
– The contextual situation (problem) is analysed and represented with a differential
equation.
– A suitable method for determining the solution is chosen.
– Initial or boundary conditions are identified and used to determine the constant of
integration.
– The differential equation is solved correctly.
– Partial derivatives are computed where necessary.
– Mathematical notation is used to communicate the results clearly
3 LECTURER(S) AND CONTACT DETAILS
3.1 Lecturer(s)
The lecturer responsible for this module is Dr. SB Mugisha. You can contact her at:
Dr. SB Mugisha
Tel: [phone]
Room no: C 6-54
GJ Gerwel Building
e-mail: [e-mail]
A notice will be posted on myUnisa if there are any changes and/or an additional lecturer
is appointed to this module.
Please do not hesitate to consult your lecturer whenever you experience difficulties with your stud-
ies. You may contact your lecturer by phone or through correspondence or by making a personal
visit to his/her office. Please arrange an appointment in advance (by telephone or by e-mail)
to ensure that your lecturer will be available when you arrive.

MAT1512/001
9
Please come to these appointments well prepared with specific questions that indicated your own
efforts to have understood the basic concepts involved. If these difficulties concern exercises
which you are unable to solve, you must send us your attempts so that we can see where you are
going wrong.
If you should experience any problems with the exercises in the study guide, your lecturer will
gladly help you with them, provided that you send in your bona fide attempts. When sending in
any queries or problems, please do so separately from your assignments and address them
directly to your lecturer.
3.2 Department
You can contact the Department of Mathematical Sciences as follows:
Department of Mathematical Sciences
Fax number: 011 670 9171 (RSA) [phone] (International)
Departmental Secretary: 011 670 9147 (RSA) [phone] (International)
e-mails: [e-mail] or [e-mail]
3.3 University
To contact the University, follow the instructions on the Contact us page on the Unisa website.
Remember to have your student number available whenever you contact the University.
Whenever you contact a lecturer via e-mail, please include your student number in the subject
line to enable the lecturer to help you effectively.
4 RESOURCES
4.1 Joining myUnisa
The myUnisa learning management system is the University’s online campus which will help you
communicate with your lecturers, other students, and the administrative departments within Unisa.
To claim your myUnisa account, Please follow the steps below:
1. Visit the myUnisa website at https://my.unisa.ac.za/portal
2. Click on the “Claim Unisa login” link on the top of the screen under the orange use ID box.
3. A new screen will load, prompting you to enter your student number. Please enter your
student number and click “continue”.
4. Enter your surname, your full name, your date of birth and, finally, your South African ID
number (for South African citizens) OR your passport number (for foreign students). Then
clock “continue”. Remember to enter either an ID number or a passport number, NOT
both.
5. Please read through the guidelines and click all the check boxes to acknowledge that you
have read all the information provided. Once you are done, click the “Acknowledge” button to
redirect you to the final page in the process.
6. The final page will display your myLife e-mail address, and your myLife AND myUnisa
password. This password will also be sent to the cellphone number displayed on the page for
safekeeping.
7. Please note that it can take up to 24 hours for your myLife e-mail account to be created.

10
Remember, the password provided is your myUnisa AND myLife password.
4.2 Prescribed book
The prescribed textbook is
James Stewart
Calculus
Metric version 8E
Early Transcendentals
Cengage Learning
ISBN 13: 978-1-305-27237-8
Please buy the textbook as soon as possible since you have to study from it directly- you cannot
do this module without the prescribed textbook.
Please refer to the list of official booksellers and their addresses in the Study@Unisa brochure.
The prescribed book can be obtained from the University’s official booksellers. If you have difficulty
locating your book at these booksellers, please contact the Prescribed Books Section at (012) 429
4152 or e-mail [e-mail].
4.3 Recommended book(s)
There are no recommended books for this module.
4.4 Electronic Reserves (e-reserves)
E-reserves can be downloaded from the Library catalogue. More information is available at:
https://libguides.unisa.ac.za/request/request
Videos for MAT1512 made by your lecturer and put on You-Tube
We managed to put online (account Youtube) the video from your Lecturer Dr. Mugisha on
Calculus A. As the video is too long we had to cut it into four parts. The videos are all about the
module MAT1512. The videos cover the sections of this module which most student tend to have
difficulties. The videos were made using an old prescribed textbook, but follow the videos with the
new prescribed textbook by James Stewart.
The students can just click on the given list below or copy and paste them on their internet browser
bar.
Video 1 - Limits
http://www.youtube.com/watch?v=GuRGhrt19tM&feature=youtu.be
video 2- Limits and continuity
http://www.youtube.com/watch?v=tEenlPFx6Mk&feature=youtu.be
Video 3-Calculus A-Differentiation
http://www.youtube.com/watch?v=Eyc7C54sPgA
Video 4-Calculus A-Integration
http://www.youtube.com/watch?v=sChEcFeuqT8
4.5 Library services and resources
The Unisa Library offers a range of information services and resources:
 for detailed Library information go to https://unisa.ac.za/library

MAT1512/001
1
1
 for research support and services (e.g. personal librarians and literature search services) go
to http://www.unisa.ac.za/sites/corprate/default/Library/Library-services/R
 The Library has created numerous Library guides:
http://libguides.unisa.ac.za
Recommended guides:
 Request and download recommended material:
http://libguides.unisa.ac.za/request
 Postgraduate information services:
http://lidguides.unisa.ac.za/request/postgrad
 Finding and using library resources and tools:
https://libguides.unisa.az.za/research-support
 Frequently asked questions about the Library:
http://libguides.unisa.ac.za/ask
 Services to students living with disabilities:
http://lidguides.unisa.ac.za/disability
 Assistance with technical problems accessing the Unisa Library or resources:
https://libguides.unisa.ac.za/techsupport
You may also send an e-mail to [e-mail] (please add your student number in
the subject line).
• for detailed Library information go to http://www.unisa.ac.za/sites/corporate/default/Library
• for research support and services (e.g. personal librarians and literature search services) go to
http://www.unisa.ac.za/sites/corporate/default/Library/Library-services/Research-support
The Library has created numerous Library guides:
http://libguides.unisa.ac.za
Recommended guides:
• Request and download recommended material:
http://libguides.unisa.ac.za/request/request
• Postgraduate information services:
http://libguides.unisa.ac.za/request/postgrad
• Finding and using library resources and tools:
http://libguides.unisa.ac.za/Research skills
• Frequently asked questions about the Library:
http://libguides.unisa.ac.za/ask

12
• Services to students living with disabilities:
http://libguides.unisa.ac.za/disability
5 STUDENT SUPPORT SERVICES
The Study@Unisa website is available on myUnisa: www.unisa.ac.za/brochures/studies
This website has all the tips and information you need to succeed at Unisa.
6 HOW TO STUDY ONLINE ?
6.1 What does it mean to study fully online?
Studying fully online modules differs completely from studying some of your other modules at
Unisa.
• All your study material and learning activities for online modules are designed to be
delivered online on myUnisa.
• All your assignments must be submitted online. This means that you will do all your activities
and submit all your assignments on myUnisa. In other words, you may NOT post your assignments
to Unisa using the South African Post Office.
• All communication between you and the University happens online. Lecturers will
communicate with you via e-mail and SMS, and use the Announcements, the Discussion Forums
and the Questions and Answers tools. You can also use all of these platforms to ask questions and
contact your lecturers.
STUDY PLAN
The table in the Tutorial Letter, which gives an Overview of the Module, indicates which sections in
the textbook cover the syllabus of the module and have to be studied.
At the beginning of each assignment there is an indication of the sections in the textbook and study
guide, which have to be studied properly before the assignment is attempted.
It is very important to study each section well at this stage. Make a good start by reading through
the text, studying each and every example and doing the indicated exercises. Study the specific
sections as if the assignment that follows, is a test of your knowledge and understanding of these
sections.

MAT1512/001
1
3
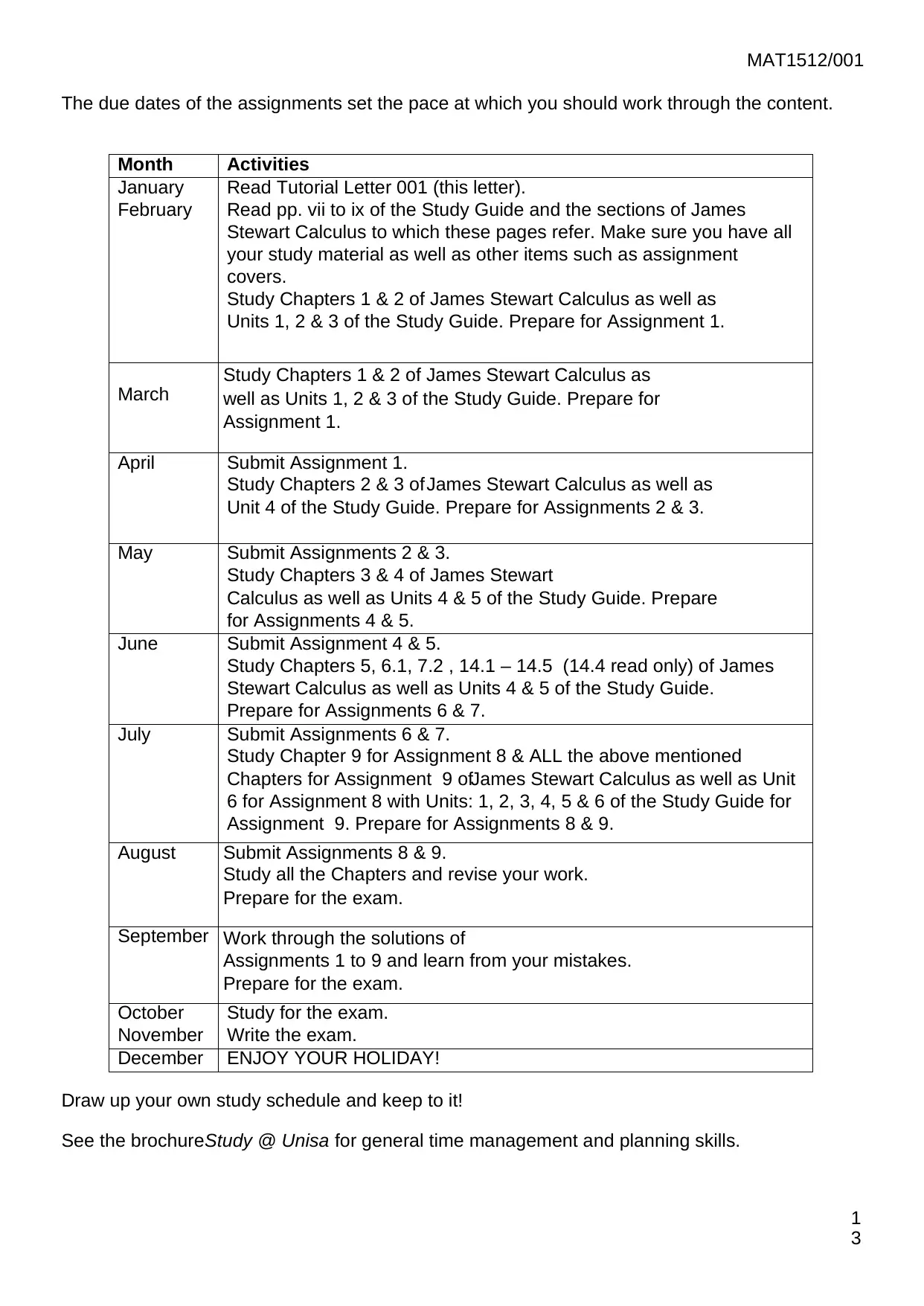
The due dates of the assignments set the pace at which you should work through the content.
Month Activities
January
February
Read Tutorial Letter 001 (this letter).
Read pp. vii to ix of the Study Guide and the sections of James
Stewart Calculus to which these pages refer. Make sure you have all
your study material as well as other items such as assignment
covers.
Study Chapters 1 & 2 of James Stewart Calculus as well as
Units 1, 2 & 3 of the Study Guide. Prepare for Assignment 1.
March
Study Chapters 1 & 2 of James Stewart Calculus as
well as Units 1, 2 & 3 of the Study Guide. Prepare for
Assignment 1.
April Submit Assignment 1.
Study Chapters 2 & 3 of James Stewart Calculus as well as
Unit 4 of the Study Guide. Prepare for Assignments 2 & 3.
May Submit Assignments 2 & 3.
Study Chapters 3 & 4 of James Stewart
Calculus as well as Units 4 & 5 of the Study Guide. Prepare
for Assignments 4 & 5.
June Submit Assignment 4 & 5.
Study Chapters 5, 6.1, 7.2 , 14.1 – 14.5 (14.4 read only) of James
Stewart Calculus as well as Units 4 & 5 of the Study Guide.
Prepare for Assignments 6 & 7.
July Submit Assignments 6 & 7.
Study Chapter 9 for Assignment 8 & ALL the above mentioned
Chapters for Assignment 9 ofJames Stewart Calculus as well as Unit
6 for Assignment 8 with Units: 1, 2, 3, 4, 5 & 6 of the Study Guide for
Assignment 9. Prepare for Assignments 8 & 9.
August Submit Assignments 8 & 9.
Study all the Chapters and revise your work.
Prepare for the exam.
September Work through the solutions of
Assignments 1 to 9 and learn from your mistakes.
Prepare for the exam.
October
November
Study for the exam.
Write the exam.
December ENJOY YOUR HOLIDAY!
Draw up your own study schedule and keep to it!
See the brochureStudy @ Unisa for general time management and planning skills.