MAT 142 Assignment 4: Film Attendance Analysis using Calculus Tools

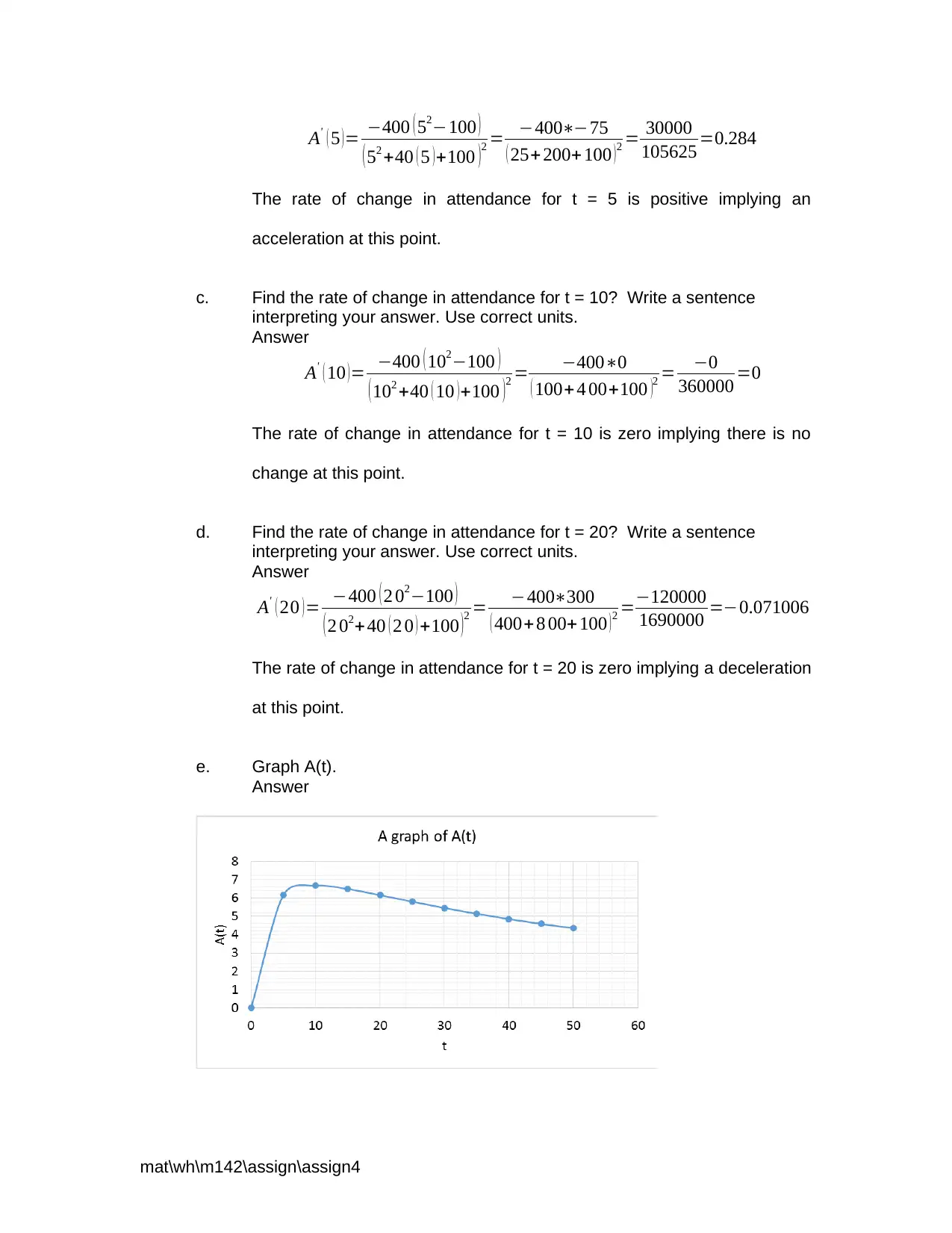
This assignment solution provides a detailed analysis of film attendance using calculus, specifically focusing on the rate of change in attendance over time. The solution uses the quotient rule to find the derivative of the attendance function, A(t), and calculates the rate of change at t = 5, t = 10, and t = 20 weeks. Each calculation is followed by an interpretation of the result, explaining whether the attendance rate is accelerating, constant, or decelerating at that point in time. A graph of A(t) is included to visually represent the changes in attendance. The analysis concludes with a paragraph describing how the attendance rate changes over time, utilizing calculus vocabulary to explain the trends observed. The assignment is from Montgomery County Community College MAT 142 course.

MONTGOMERY COUNTY COMMUNITY COLLEGE
MAT 142
Assignment 4
Name _____________________________
Every assignment must be typed and a sufficient amount of work shown. Graphs must
be done electronically (I do not want hand drawn graphs.) Directions for graphing using
excel are available in blackboard.
You may ask for help with the assignments.
Advertising and sales. An excellent film with a very small advertising budget must
depend largely on word-of-mouth advertising. If attendance at the film after t weeks is
given by
,
And A is in hundreds of thousands.
a. Use the quotient rule to find and simplify the numerator.
Answer
A' ( t ) = d
dt [ 400 t
t2+ 40 t+100 ]
¿ 400. d
dt [ t
t2 +40 t +100 ]
¿ 400
d
dt [ t ] . ( t2+ 40 t+ 100 ) −t . d
dt [ t2+40 t+100 ]
( t 2+40 t+100 ) 2
¿ 400
t2 +40t +100 − 400 t (2t + 40)
( t2 +40 t+100 ) 2
A' ( t ) =−400(t2−100)
( t2 +40 t+ 100 ) 2
b. Find the rate of change in attendance for t = 5? Write a sentence
interpreting your answer. Use correct units.
Answer
mat\wh\m142\assign\assign4

A' ( 5 )= −400 ( 52−100 )
(52 +40 ( 5 )+100 )2 = −400∗−75
( 25+200+ 100 )2 = 30000
105625 =0.284
The rate of change in attendance for t = 5 is positive implying an
acceleration at this point.
c. Find the rate of change in attendance for t = 10? Write a sentence
interpreting your answer. Use correct units.
Answer
A' ( 10 ) = −400 ( 102−100 )
( 102 +40 ( 10 ) +100 )
2 = −400∗0
( 100+ 4 00+100 )2 = −0
360000 =0
The rate of change in attendance for t = 10 is zero implying there is no
change at this point.
d. Find the rate of change in attendance for t = 20? Write a sentence
interpreting your answer. Use correct units.
Answer
A' ( 20 )= −400 ( 2 02−100 )
(2 02+ 40 ( 2 0 ) +100 )2 = −400∗300
( 400+8 00+100 )2 =−120000
1690000 =−0.071006
The rate of change in attendance for t = 20 is zero implying a deceleration
at this point.
e. Graph A(t).
Answer
mat\wh\m142\assign\assign4

f. Write a paragraph describing how the attendance changes, make sure
you use the results from parts a, b, and c. Use calculus vocabulary.
Answer
Attendance rate increases between time t=0 and time t = 10 before it
starts decelerating. This is evident as can be seen when t = 5 the rate is
positive but it comes to negative at t = 10.
mat\wh\m142\assign\assign4