Maths 1 Assignment: Detailed Solutions for Calculus and Analysis

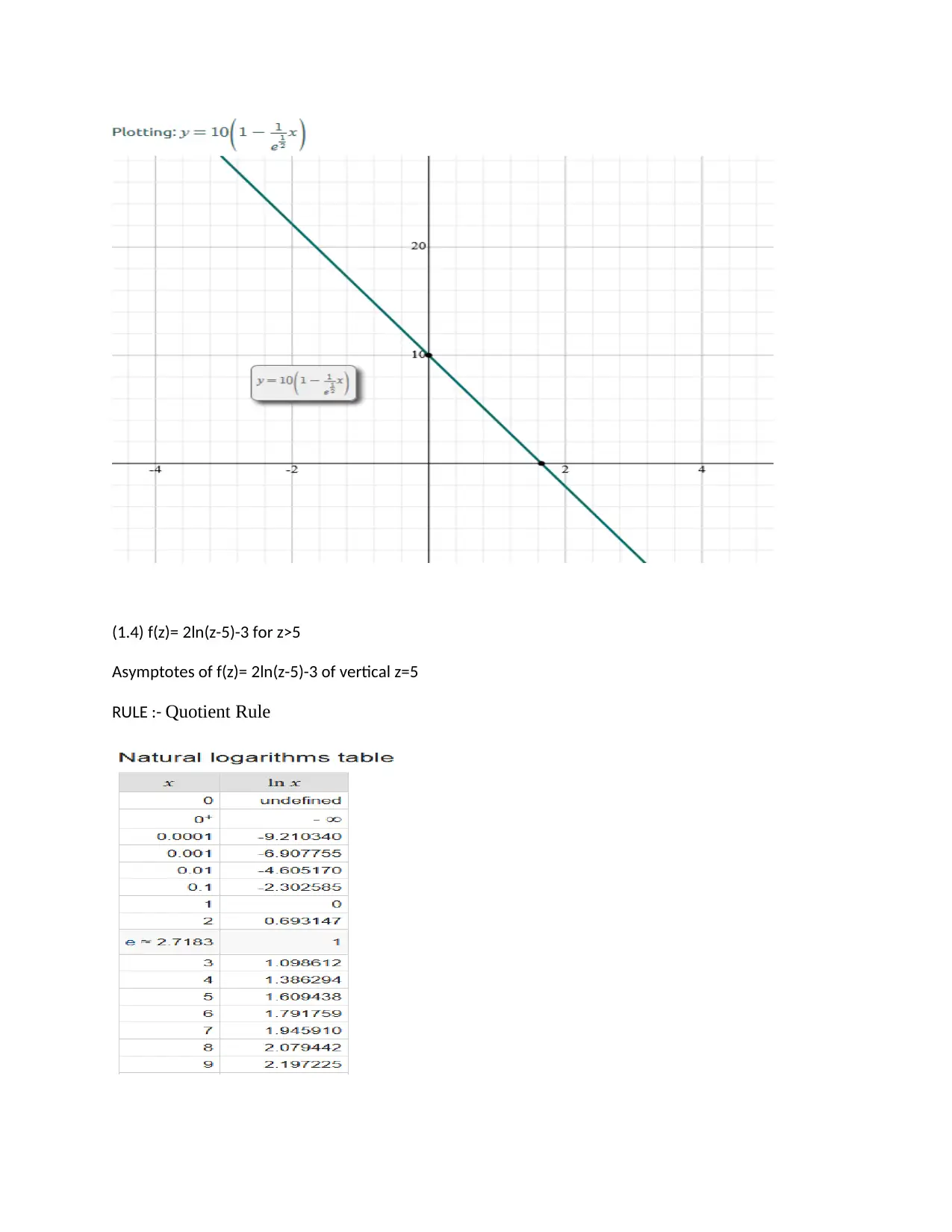
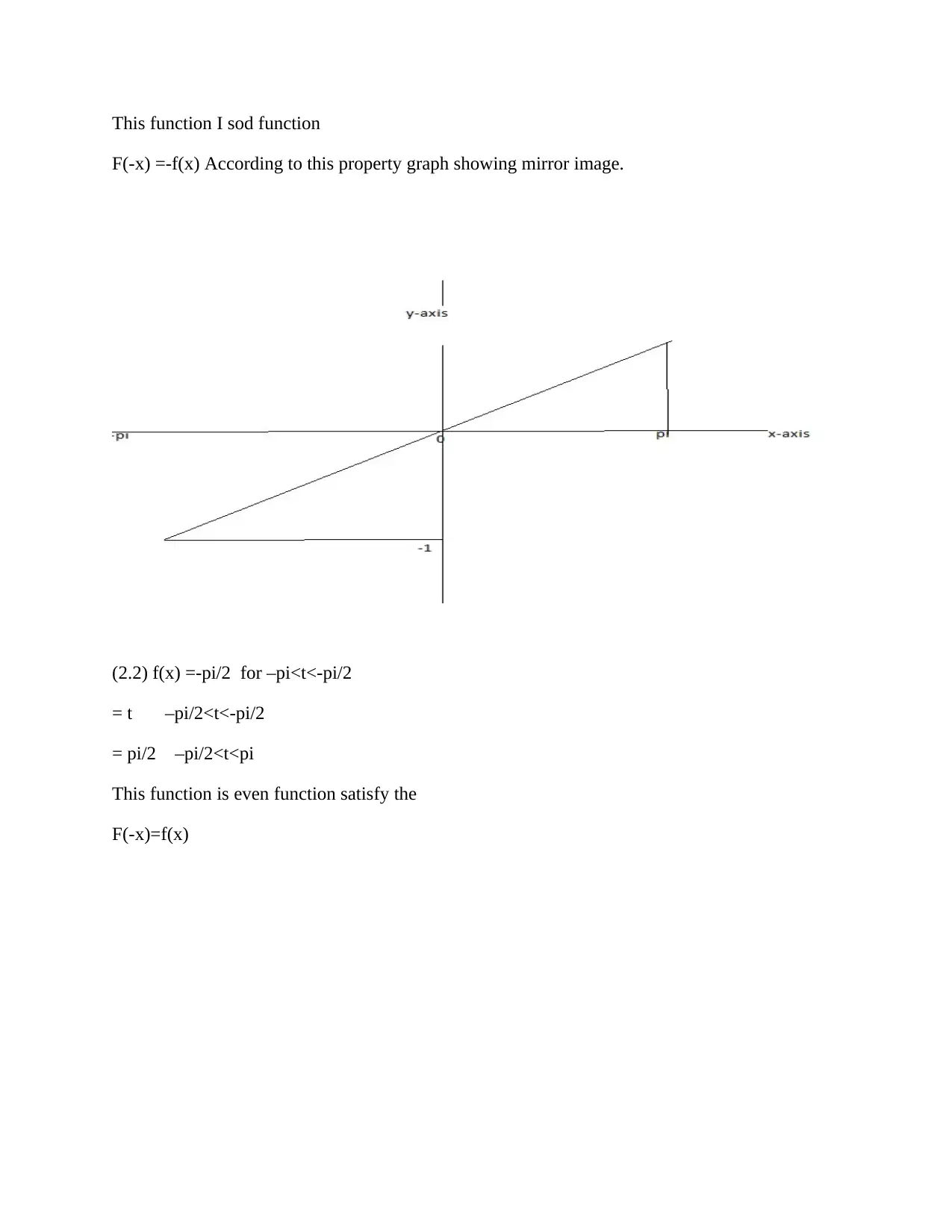
This document presents a comprehensive solution to a Maths 1 assignment, encompassing a variety of calculus and analysis problems. The solutions cover topics such as plotting graphs of different function types (algebraic, trigonometric, and exponential), including the identification of extreme points and asymptotes. It also includes the analysis of even and odd functions, along with problems related to exponential decay, trigonometric functions, and the application of integration to find average values and volumes. Furthermore, the assignment delves into the Simpson's rule for integration and numerical methods like the bisection and Newton-Raphson methods for finding roots of equations. The solutions demonstrate the application of various formulas and techniques, providing a detailed step-by-step approach to solve each problem.

Maths

1 Solution:-
1.1F(x) = 3x3-4
Extreme point at (0,-4)
Simple Rule for plot the graph is ‘Bivariate’ plot. One axis is horizontal axis along the "x-axis and
other is the vertical axis is the "y-axis". X- axis represents the 3x3-4 function value and y axis shows
f(x).
(1.2) f(t) = 3- 2 sin(t+pi/3)
Rule is Basic trigonometry function.
For this plot transform and translate trig functions into basic algebra. X-axis represent the variation in
time whereas y axis represents the amplitude of trigonometry function sin x.

(1.3) f(t) =10(1-e(-1/2)t)
To plot the graph in the exponential form is difficult as compared to algebraic. So convert exponential
value in the decimal. So all of its y-values will be decimal approximations
Rule: A number with a negative exponent is the reciprocal of the number to the corresponding
positive exponent.

(1.4) f(z)= 2ln(z-5)-3 for z>5
Asymptotes of f(z)= 2ln(z-5)-3 of vertical z=5
RULE :- Quotient Rule

Quotient rule ln(x / y) = ln(x) - ln(y)
Horizontal : None
Axis intercept at x axis are (e3/2+5,0)
Extreme points :None
2Solution:-
2.1 F(x) =1 for 0<t<pi
F(x) =-1 for –pi<t<0

This function I sod function
F(-x) =-f(x) According to this property graph showing mirror image.
(2.2) f(x) =-pi/2 for –pi<t<-pi/2
= t –pi/2<t<-pi/2
= pi/2 –pi/2<t<pi
This function is even function satisfy the
F(-x)=f(x)

3. Solution:-
Function of this graph: N(t) = Noe-kt
Higher the value of K faster will be the decay.
we can define a constant: τ (Time constant) = 1/k
τ (Time constant) =26
τ is the decay the “time constant” of the Capaictor
Rewrite function:: N(t) = Noe-t/τ
Therefore According to the graph
N(t) = Noe-26t
N(t) = Noe-26t [ from the graph No = 3 and τ =26]
N(t) = 3e-26t
4 Solution:-
According to the given graph

It relates with the equation
Y =A cos(B(x+D))+C)
For getting value of A,B,C,D
C is centre=5 (from the graph)
Amplitude(A) =7.5
PERIOICITY(B)=
PERIOD :5PI/6-PI/6
2pi/B=5PI/6-PI/6 (on comparing)
B= 3
D=pi/4 (Phase)
Put these value in equation we get
Y =7.5cos((3x+pi/4))+5)

5. Solution:-
Vavg = 1/T ∫v(t) dt
Vavg = 1/4∫v(t) dt AT LIMIT 2 TO 6
Vavg = ¼(limit 2 to 4 ∫v(t) dt + limit 4 to 6 ∫v(t) dt)
Vavg =¼(limit 2 to 4 ∫10 dt + limit 4 to 6 ∫20( dt)
=¼[(10(4-2) + 20(6-4)]
=¼(20+40)

=15
6. Solution:- Volume by the integral method
V=at limit 0 to 14∫A.dx
V=at limit 0 to 14∫pi.r2dx
Diameter = 3.2+4.6+4.8+6.4+6.4+6.5+6.7
=45.5
Radius= Diameter/2
=22.75
V=at limit 0 to 14∫pi.r2dx
=3.14*(22.75*22.75)[14-0]
V=22752m^3
7. Solution:-
Graph:-Angular Velocity vs Time
(2.)

formulas: 90 = (b, -a); 180 = (-a, -b); 270 = (-b, a); 360 = (a, b).
No. of rotations =4
At points (0,10), (0,-10)
Mid ordinate Rule:-
Average
Velocity
6.5 8.0 10.1 10.9 11.1 9.7 8.3 0
Time 0 1 2 3 4 5 6 7 8
Mid coordinate rule
Area (A) = average area * Base length
Area(A)= (H1D+H2D+H3D+H4D+H5D+H6D+H7D+H8D)/nD
H1= Height of coordinate vertical axis.
D= distance between two coordinates in X axis.
N= no. of coordinates
Area(A)=D[h1+h2+h3+h4+h5+h6+hh8}/nD
Therefore Area(A) = (6.5*1+8*1+10.1*1+10.9*4+11.1*1+9.7*1+8.3*7+0*8)/8
Area= 64.8/8 m^2
Area= 8.1 m^2
7(3) 360° = (2π)radians, or
1 radian = (360°/2π) = 57.3°,
360/2π = 90/x
360x = 180π
x = ω = π/2 [w =angular vrelocity)
The answer is one-half pi radians per second.
8 Solution:-

8(b) Solution:- Simpson Rule for
Limit 0 to 4∫et^2/9dt n=8
Formula:- Limit 0 to 1 ∫f(x)dx = deltaX = [f(x0)+4f(x1)+2f(x2)+……+2f(x)n-2 +4fx(n-
1)+f(x)n]
F(x)= et^2/9dt
deltaX =(b-a)/n
b=4
a=0
n=8
deltaX = 4-0/8

deltaX =1/2
S8 =0.5/3[e0.5^2+ e0.10^2+ e0.15^2+ e0.20^2+ e0.25^2 +e0.30^2+ e0.35^2+ e0.40^2]
S8 =0.5/3[e0.25+ e0.01+ e0.0225+ e0.04+ e0.0625 +e0.09+ e0.1225+ e0.16]
S8 =0.5/3[1.28402+ 1.01005 ++1.02275+1.04081+1.06449+1.09417+1.130+1.17351]
S8 =0.5/3[8.8198]
S8 =1.4666666669
9 Solution :-
t4+5t-20 for t>=0
F(X) >= (5/4)4/3-5 cuberoot of (5/4)-20
Interval of function = (5/4)4/3-5 cuberoot of (5/4)-20, infinity
X- intercept at (1.18172,0) (-2.376,0)
X- intercept at (0,-20)

(2.1) Bisection method :-
t4+5t-20 for t>=0
f(0)<0
f(1)<0
f(2)>0
f(1.5)<0
f(1.8)<0
f(1.9)>0
F(1.77)>0
S.no. a(-) b(+) X(sign)
1 1.8 1.9 X0=(1.8+1.9)/2
=1.77 sign: +ve
Replace it with
positive value
because on

putting value
f(1.77) gives
positive value.
2 1.8 1.77 X0=(1.8+1.77)/2
Sign +ve
1.785 (same as
above)
3 1.8 1.785 X0=(1.8+1.785)/2 1.795(same as
above)
4 1.8 1.795 X0=(1.8+1.795)/2 1.79625
5 1.8 1.79625 X0=(1.8+1.79625)/2 1.798125
6 1.8 1.798125 X0=(1.8+1.798125)/2 1.796225
Ans is =1.79
(2.2) Newton Rapson method :
t4+5t-20 for t>=0
Can be find maximum upto 5 decimal value
F(t) =t4+5t-20
To find the root range
FOR POSTIVE VALUE- OPPSIT SIGN CHANGE GIVES THE ONE ROOT
F(0)=-20
F(1)=-14
F(2)=6
Therefore ist root lies between 1 and 2
Put t=1.8
F(1.8) = -ve [-0.524]
F(1.9)=+ve[2.7321]
Take smallesr value
F(1.8)
F(t) =t4+5t-20
Take ist derivative
F’(t) =4t3+5

F(1.8) = 4(1.8)3+5
=28.328
According to the formula:
Xn+1 =xn-(f(xn))/(f’(xn))
In form of t we can write it as
ti+1=ti- ( ti4+5ti-20) /(4ti3+5)………………….(1)
on solving equation (1) we obtain
ti+1 = (3ti4+20)/(4t3+5)………………………..(2)
On putting the value of t=1.8 in equation(1) we obtained
ti+1 = (3(1.8)4+20 )/(4(1.8)3+5)
Ist decimal place value- ti+1 = 51.49/28.328
ti+1 = 1.8413……………………..Now put this value in the equation …(2)
2nd decimal place value
ti+1 = (3(1.8413)4+20)/(4(1.8413)3+5)
ti+1 = 52.98/28.88
ti+1 = 1.83448……….. Now put this value in the equation …(2) again
3rd decimal place value
ti+1 = (3(1.83448)4+20)/(4(1.83448)3+5)
ti+1 = 53.97/29.69
ti+1= 1.8177……….. Now put this value in the equation …(2) again
4th decimal place value
ti+1 = (3(1.8177)4+20)/(4(1.8177)3+5)
ti+1=52.74/29.02
ti+1=1.817367……….. Now put this value in the equation …(2) again
5th decimal place value

ti+1 = (3(1.817367)4+20)/(4(1.817367)3+5)
ti+1 = 52.75/29.009
ti+1 = 1.818401
Therefore ans. is 1.81