Calculus Assignment Solution: University Level Problems

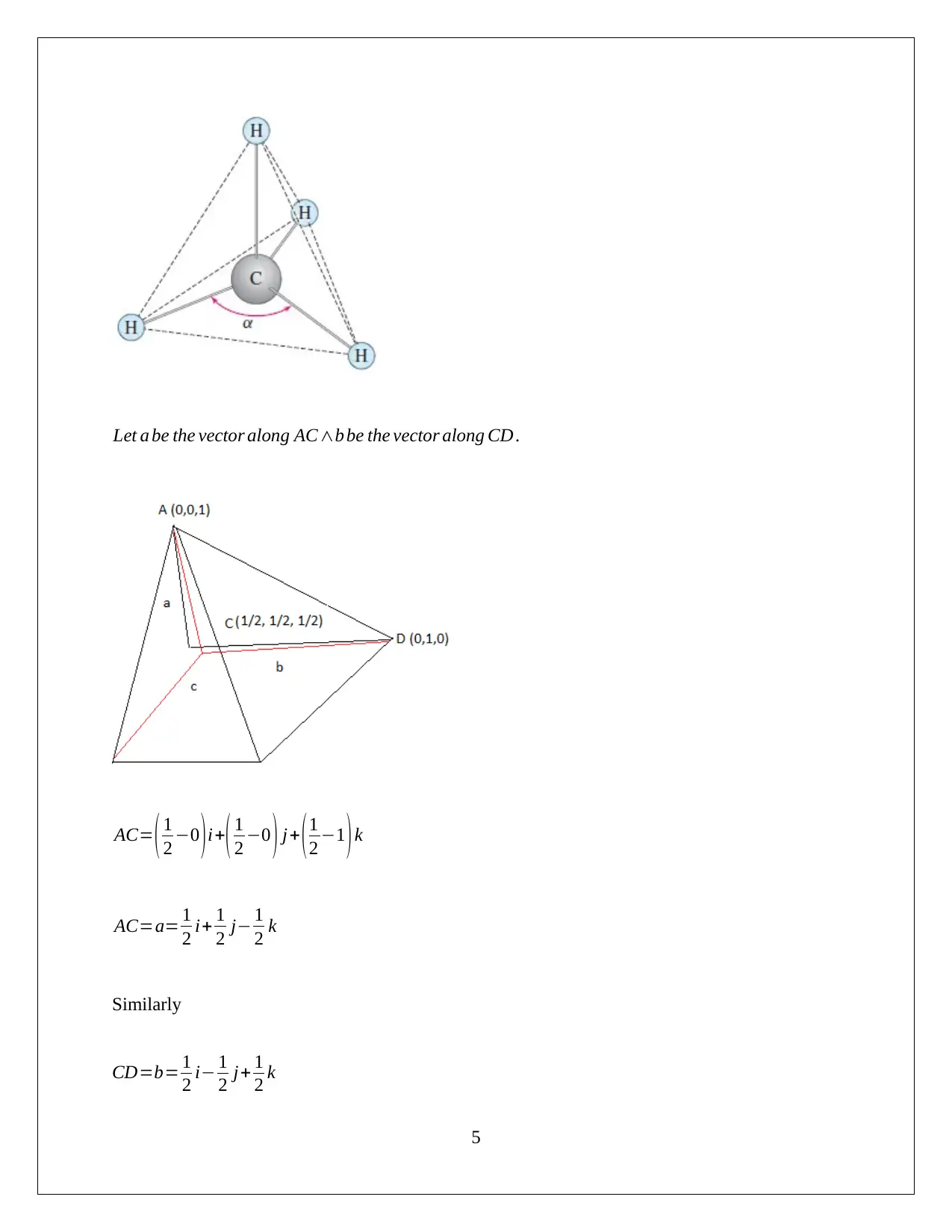
This document presents a complete solution to a calculus assignment, addressing a variety of problems. The solutions cover topics such as finding the point on a line closest to the origin, determining perpendicular unit vectors, calculating angles between vectors in a molecule, working with coordinate systems, proving midpoint relationships, applying cross and dot product rules, determining the volume of a parallelepiped, calculating the area of a triangle, and deriving equations of planes in both scalar and vector forms. The assignment also includes problems on finding plane equations passing through three points or parallel to a given plane, and determining conditions for parallel planes. Each question is solved step-by-step with explanations, making it a valuable resource for students studying calculus.

CALCULUS
Student id
[Pick the date]

Question 1
Let
Vector 1=a
Vector 2=v
Point located on the line ( a+ tv ) which is near to the origin in such as way that a ┴ v .
a ┴ vonly when the dot product would be equal to zero.
a . v =0
Line equation ¿ a+ t v
The distance (t , a+t v) from origin (0, 0) would be determined as shown below:
¿ √ ( a−c ) 2+ ¿ ¿
a=a , b=a+tv ,c =0 , d=0
¿ √ ( t−0 ) 2 +¿ ¿
¿ √ t2 +¿ ¿
Now,
let
1

f ( x )= √t2 +¿ ¿
It is essential to minimize the square of the distance and hence,
g ( x )=t2+¿
The next step is to determine the first derivative of f ( x ) .
d
dx f ( x )= d
dx ¿
¿ t +v (a+tv)
√t2+¿ ¿ ¿
Further, find the first derivative of g ( x )
d
dx g ( x ) = d
dx t2 +¿
¿ 2 t+¿
Let the value of denominator close to zero.
t2+ ¿0 (derivative is defined)
t=0 , a+tv=0∨t=−a
v
This is termed as critical point of the and therefore, point (−a
v ,0 ¿
is not close to the origin.
2

Question 2
All unit vectors which are perpendicular to the vector ( 5
12 )=?
Let the vector is a = 5i +12 j
Two vectors would be termed as perpendicular to each other when their dot product would be
equal to zero.
cos θ= a . b
|a||b|
θ=90 ° ( perpendicular )
a . b
|a||b|
=cos 90=0
a . b=0
Assume that vector (ai+bj) is perpendicular to (5i +12 j).
Now,
¿ ( ai+bj ) .(5 i+ 12 j)
3

5 a+12 b=0 … … …… . ( 1 )
In order to determine the unit vector which would be perpendicular to the (5i +12 j) hit and trial
method needs to be applied.
at a=12 , b=−5
( 5∗12 )+ ( 12∗−5 ) =0 satisfied
u1= 12i−5 j
√ ( 12 )2+ (−5 )2 =( 12i
13 − 5 j
13 )
At a=−12, b=5
¿
u2= −12 i+ 5 j
√ (−12 )2 + ( 5 )2 =(−12 i
13 + 5 j
13 )
Hence, the two unit vectors i.e. ( 12i
13 − 5 j
13 ) and ( −12i
13 + 5 j
13 ) are perpendicular to ( 5
12 ) .
Question 3
Angle between any of the two line segment from carbon atom to hydrogen atom =?
4

Let a be the vector along AC∧b be the vector along CD .
AC= ( 1
2 −0 )i+( 1
2 −0 ) j+ (1
2 −1 )k
AC=a= 1
2 i+ 1
2 j− 1
2 k
Similarly
CD=b= 1
2 i− 1
2 j+ 1
2 k
5

Now
cos θ= a . b
|a||b|
cos θ= ( 1
2 i+ 1
2 j− 1
2 k ) . ( 1
2 i− 1
2 j+ 1
2 k )
√ ( 1
2 )
2
+( 1
2 )
2
+(−1
2 )
2
√ (1
2 )
2
+( −1
2 )
2
+( 1
2 )
2
¿
1
4 − 1
4 − 1
4
√ 3
4 √ 3
4
¿
−1
4
3
4
¿− 4
12
cos θ=−1
3
θ=cos−1
(−1
3 )
θ=121.6 °
Hence, the angle would be 121.60.
6

Question 4
Given figure
Let the center of the systemO(0,0,0)
And the corner would be A ( ± 1, ± 1, ± 1 )
Hence, the by co-ordinate system as per the figure is highlighted below:
OA= (−1i+1 j+1 k )
OB= (−1 i+ 1 j−1 k )
OA .OB = ( −1i+1 j+1 k ) . ( −1 i+1 j−1 k )
¿ 1+1−1=1
Hence,
|OA|= √ (−1)2 +(1)2+(1)2= √ 3
7

|OB|= √ (−1)2+(1)2 +(−1)2 = √ 3
Now,
OA .OB =|OA||OB|cos β
cos β= OA .OB
|OA||OB|
cos β= 1
√3 × √3 = 1
3
β=cos−1
( 1
3 )
β=78.36 °
Question 5
It is given that P and Q points are located in R3.
The aim is to prove that R is the midpoint of PQ only when X is equidistant from P and Q and
XR is orthogonal to PQ.
Let the X = ( x , y , z )
Point X is equidistance from P and Q and hence, vector XR is orthogonal to PQ.
8

XR . PQ=0…………….. (1)
Here,
XR=XO +¿
Hence,
XR . PQ=0
( XO +¿ ¿ . PQ=0
XO . PQ +¿ . PQ=0
( −OX ) . PQ +¿ . PQ=0
OX . PQ=¿ . PQ … … …… … …… .. ( 2 )
Further,
PQ=PO+ OQ
R is midpoint of PQ and hence, ¿= PQ
2 = OP+OQ
2
9

From equation (2)
OX . PQ=¿ . PQ
OX . PQ=( OP +OQ
2 ).(PO +OQ)
PO=−OP
OX . PQ=( OP +OQ
2 ) .( OQ−OP )
OX . PQ= 1
2 (OP2−OQ2)
This is the equation of the plan on which x lies and hence, the above assumptions that X is
equidistance from P and Q and hence, vector XR is orthogonal to PQ. Also, R is the midpoint of
PQ and therefore, P and Q points are located in R3 .
Question 6
Cross product
10

¿ (2
0
0 )× (−1
0
1 )
¿
¿ ( 2 0 0 ) × ( −1 0 1 )
Rule of cross product of the two vectors
¿ ( 0.1−0.0 0.(−1)−2.1 2.0−0.(−1) )
¿ ( 0−0 0−20−0 )
¿ ( 0−2 0 )
¿ (−
0
2
0 )
11