University Calculus MATH 22981 Assignment 1: Limits and Viscosity
VerifiedAdded on 2022/08/21
|10
|540
|11
Homework Assignment
AI Summary
This document presents a solution to a Differential Calculus assignment (MATH 22981) focusing on the kinetic theory of gases and the analysis of limits. The assignment begins with a problem that requires students to determine the values of constants using linear regression based on experimental data related to gaseous viscosity and temperature. The solution includes plotting the function and deriving the values of the constants. The second part of the assignment involves evaluating limits, both at infinity and at finite points, providing detailed elaborations and graphical support for each answer. The solution demonstrates the application of limit theorems and algebraic manipulations to determine the behavior of functions. The document also includes references to relevant calculus textbooks. This comprehensive solution aims to assist students in understanding and solving complex calculus problems.
1 out of 10

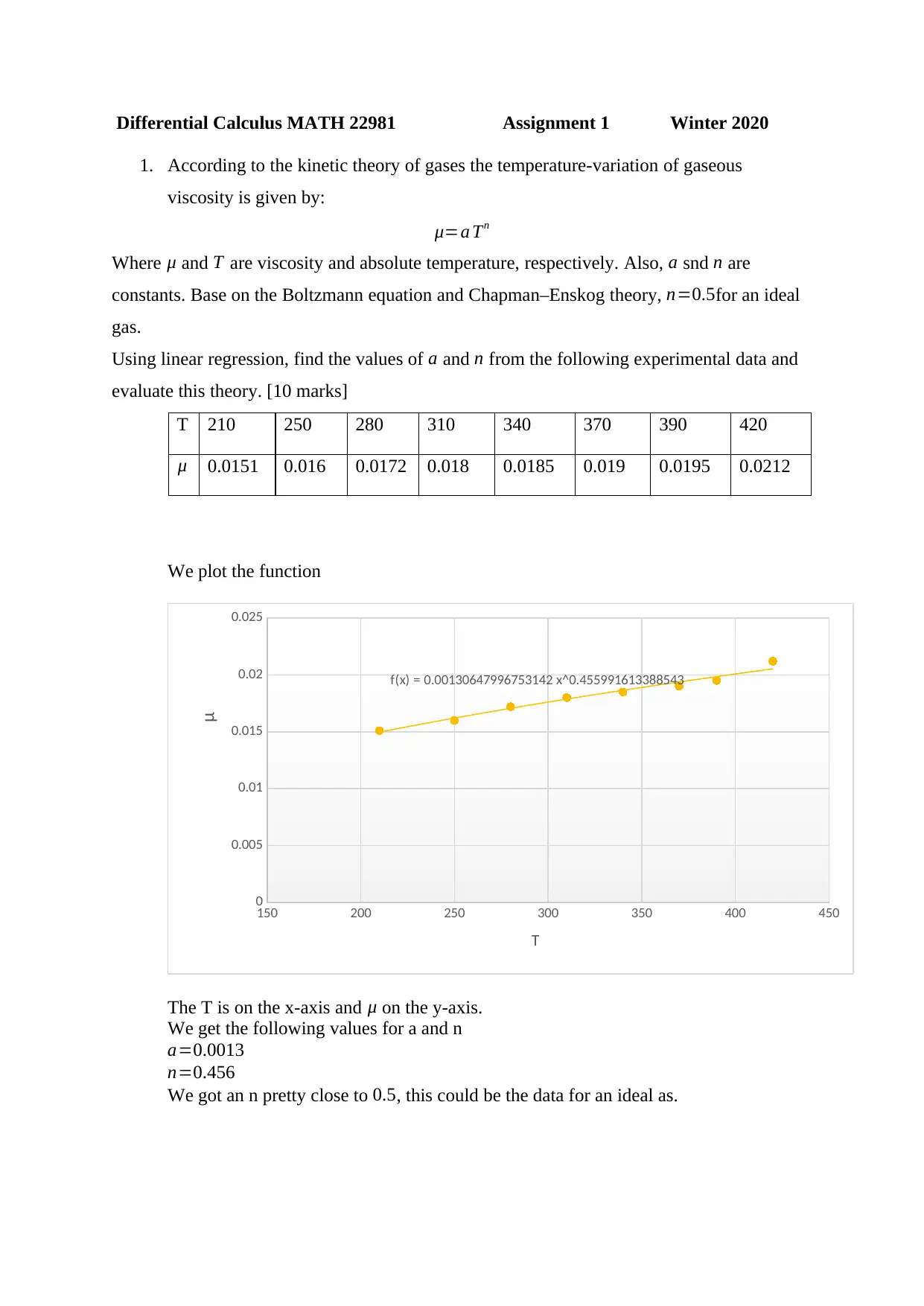
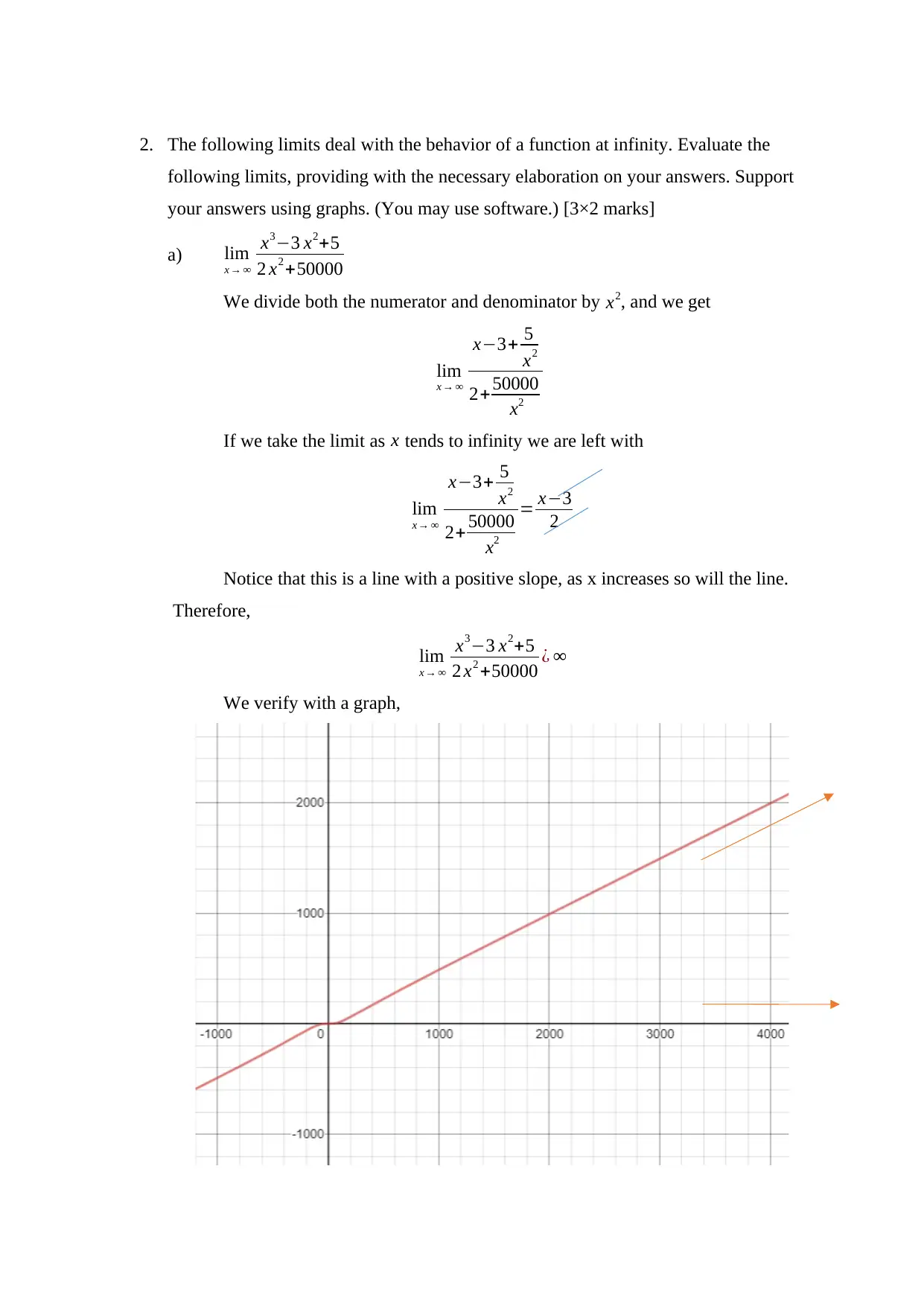


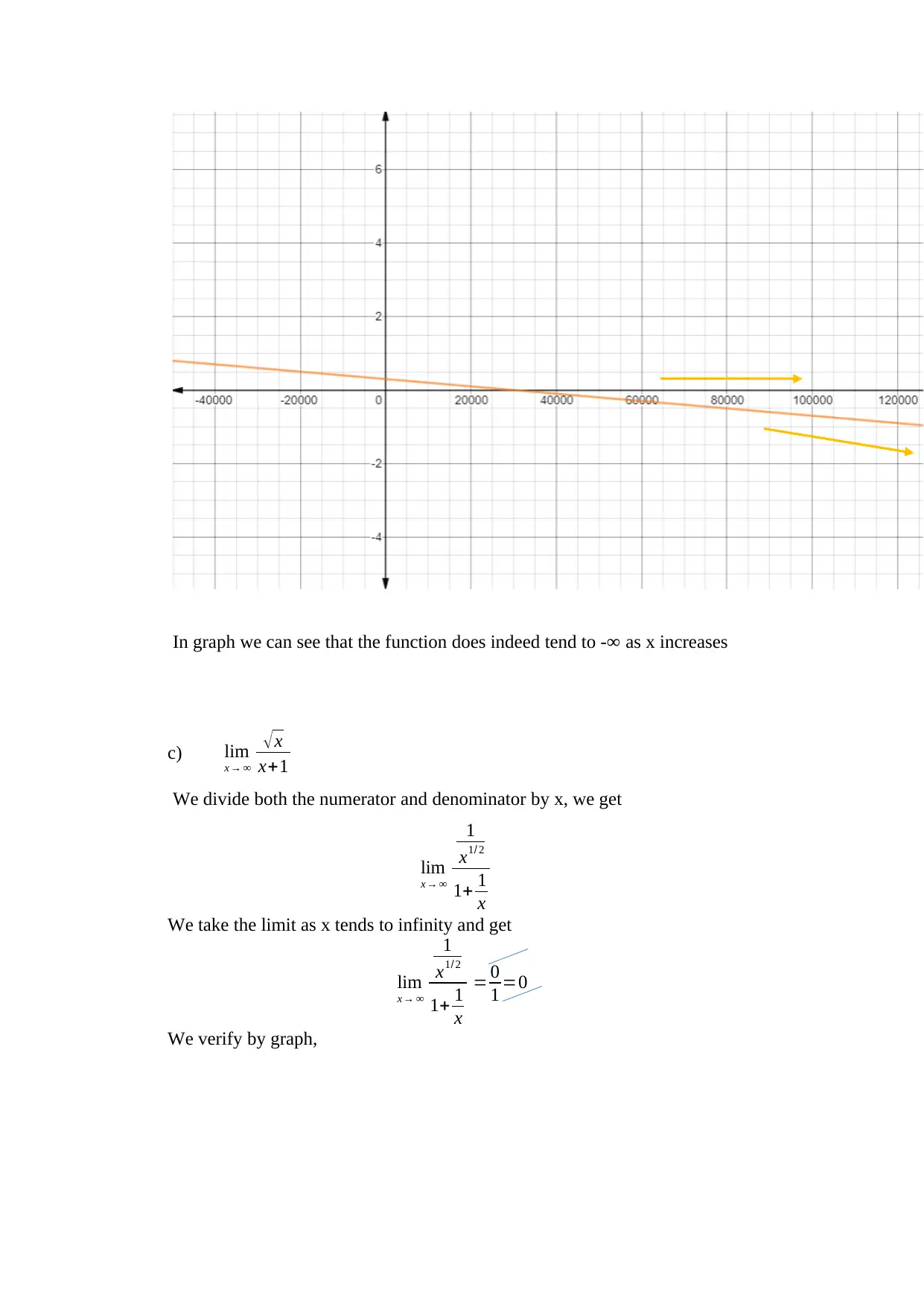
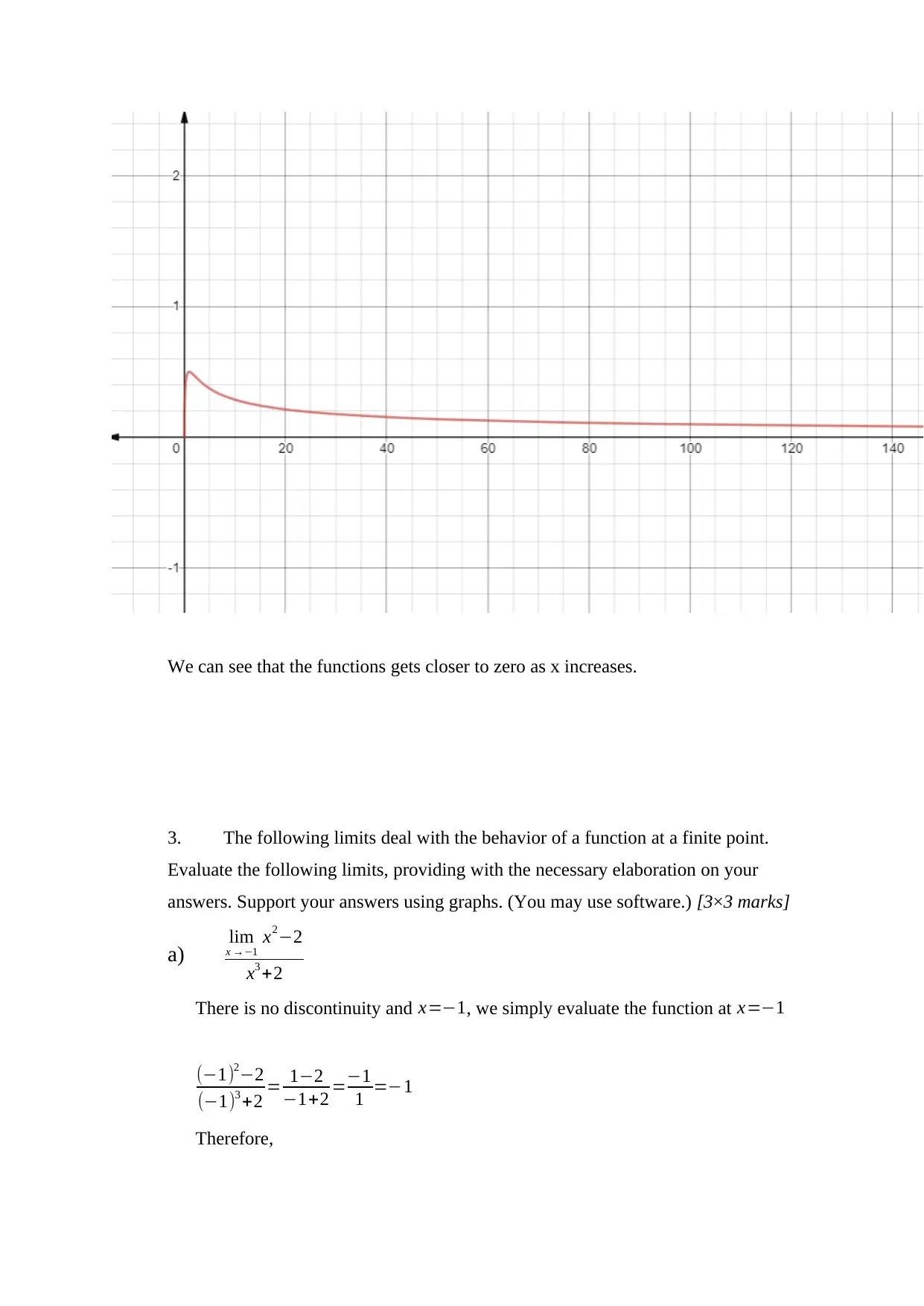
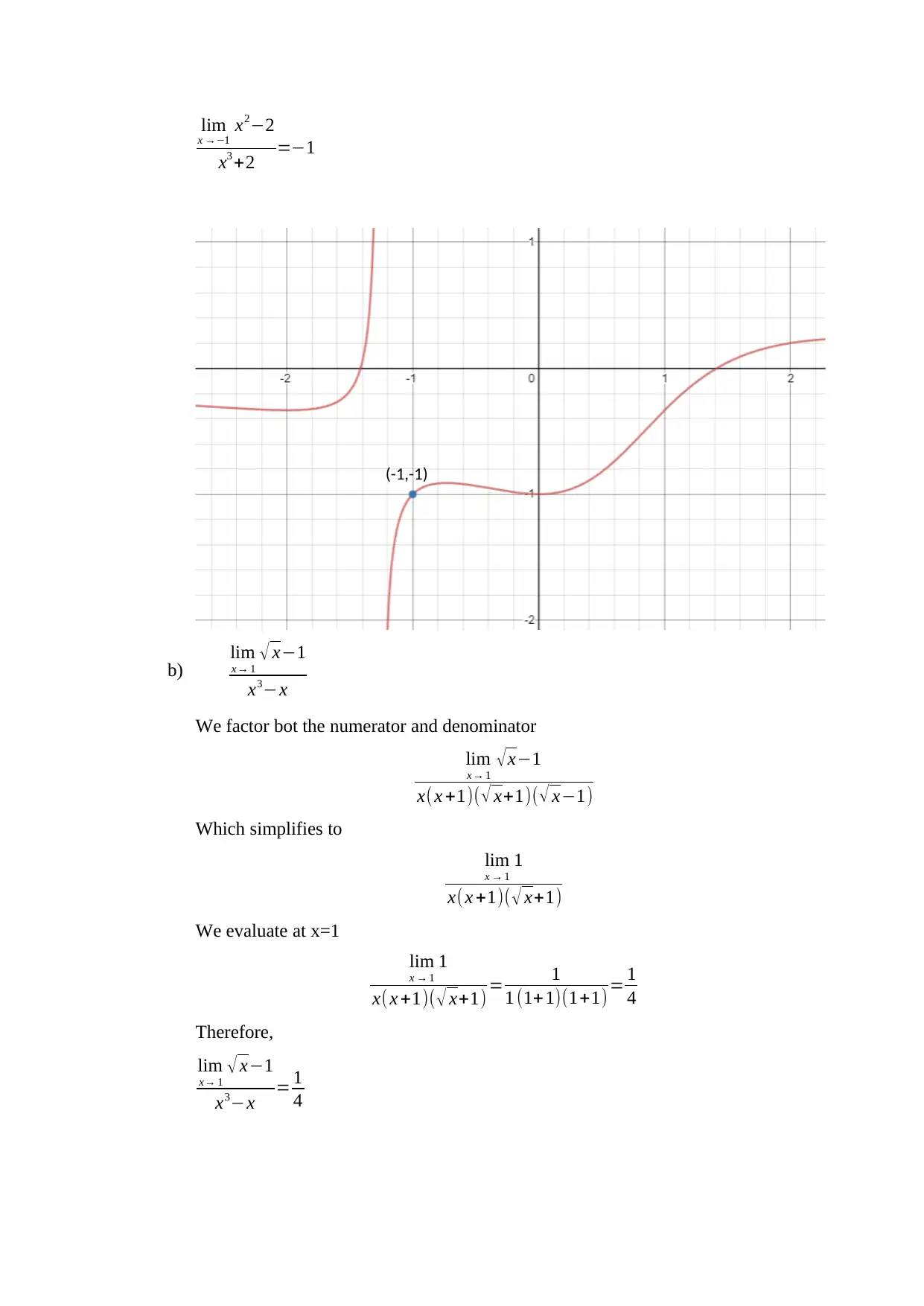
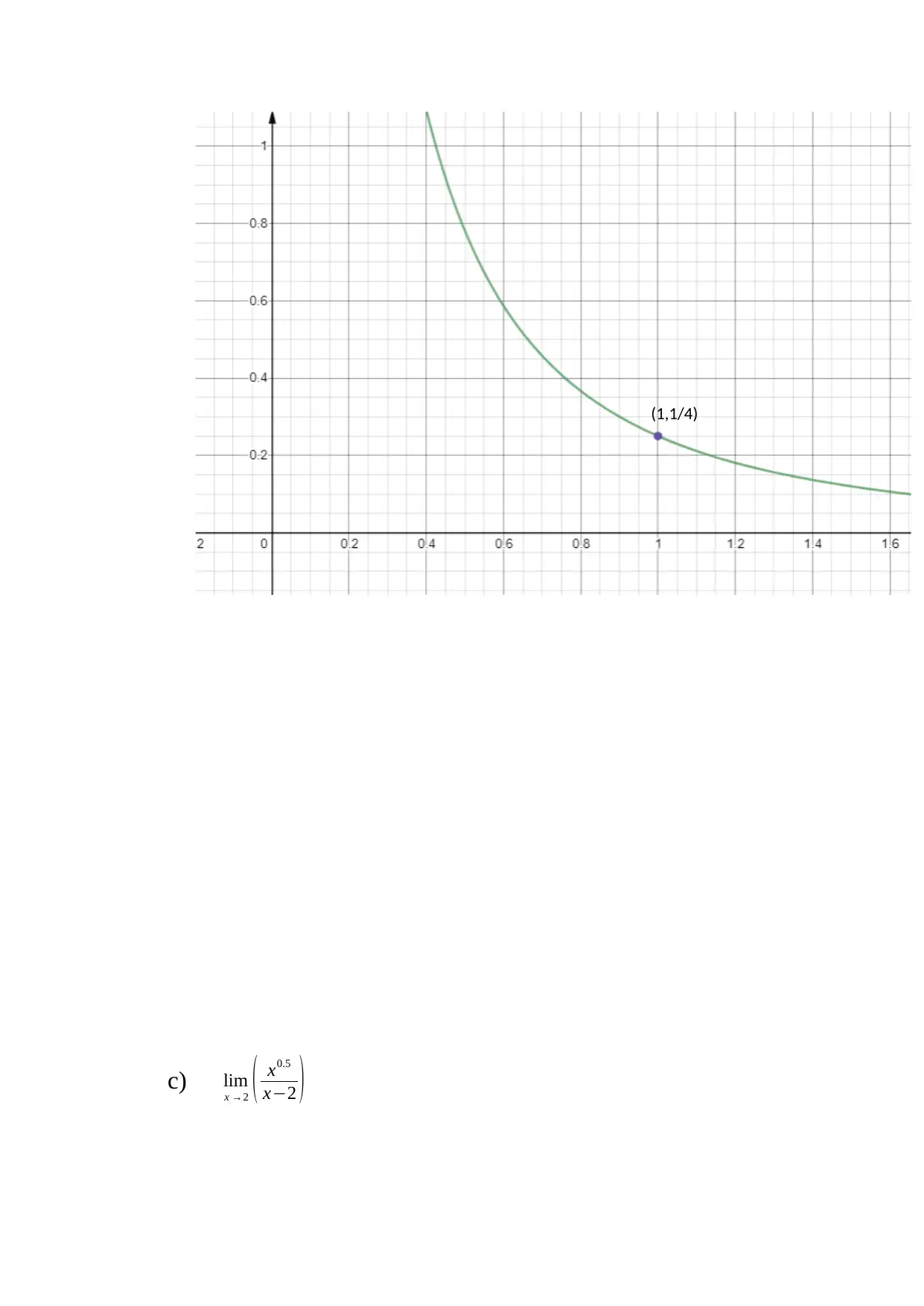
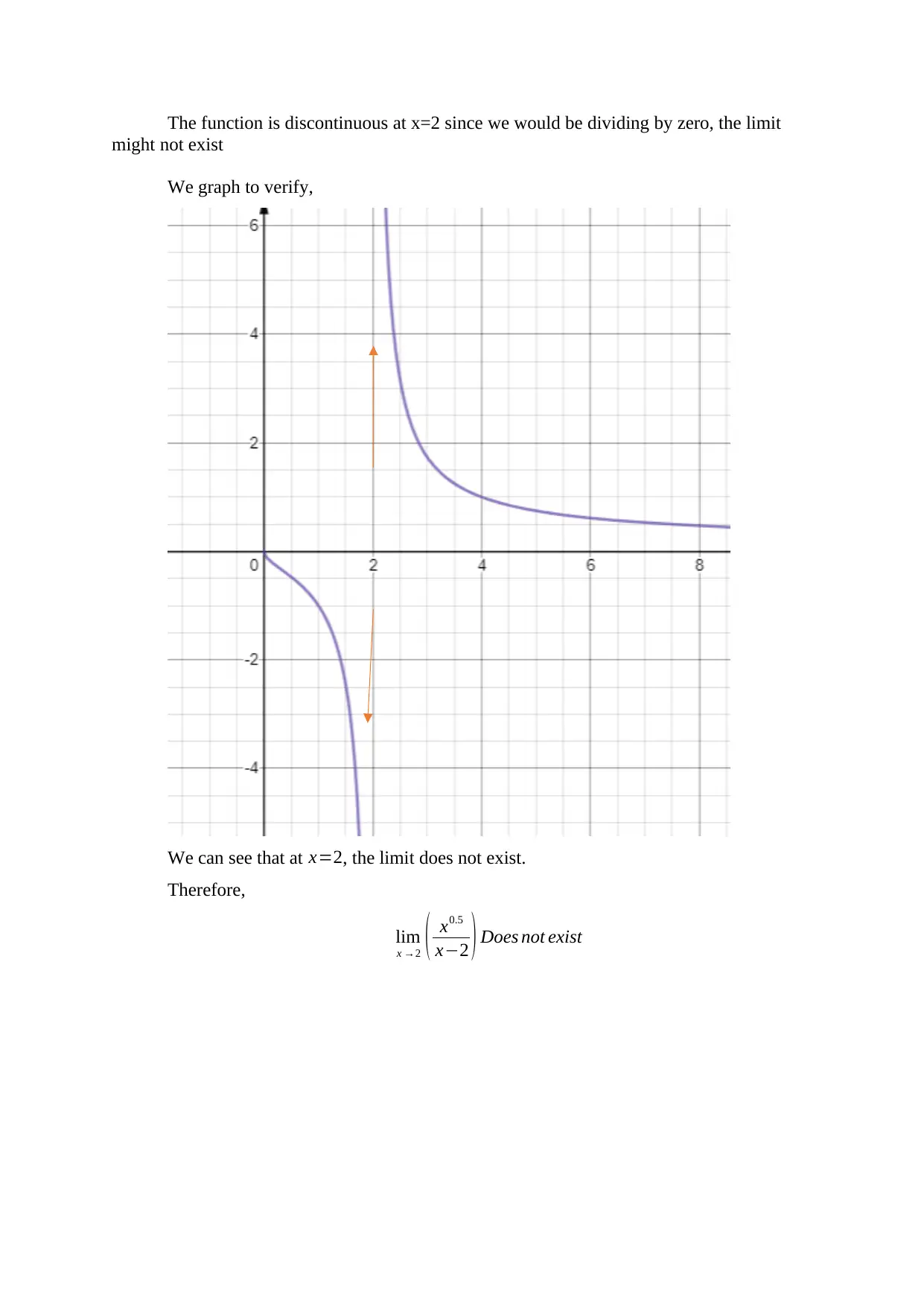



![[object Object]](/_next/static/media/star-bottom.7253800d.svg)