MAT2100 Assignment 2, University Calculus: Comprehensive Solutions
VerifiedAdded on 2020/04/07
|29
|618
|231
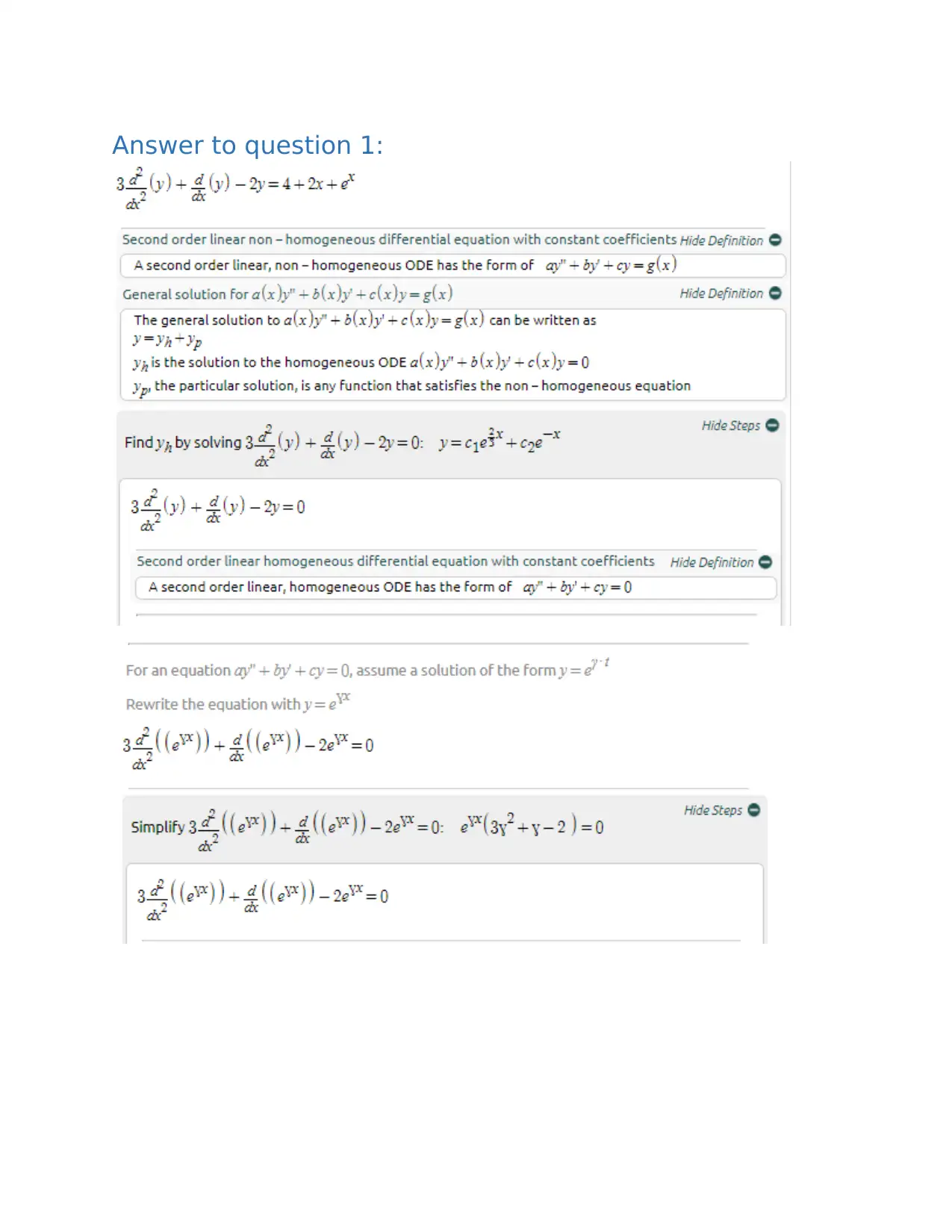
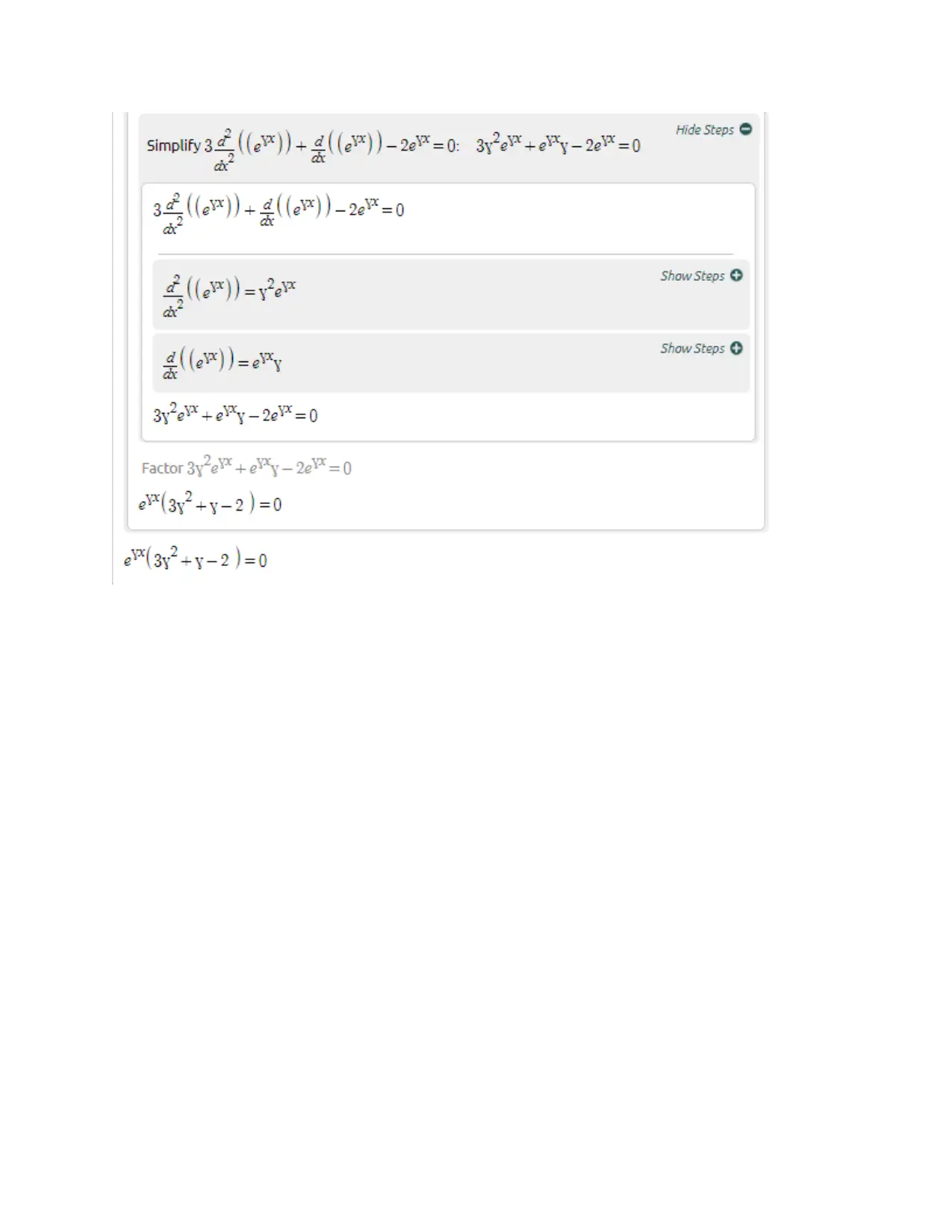
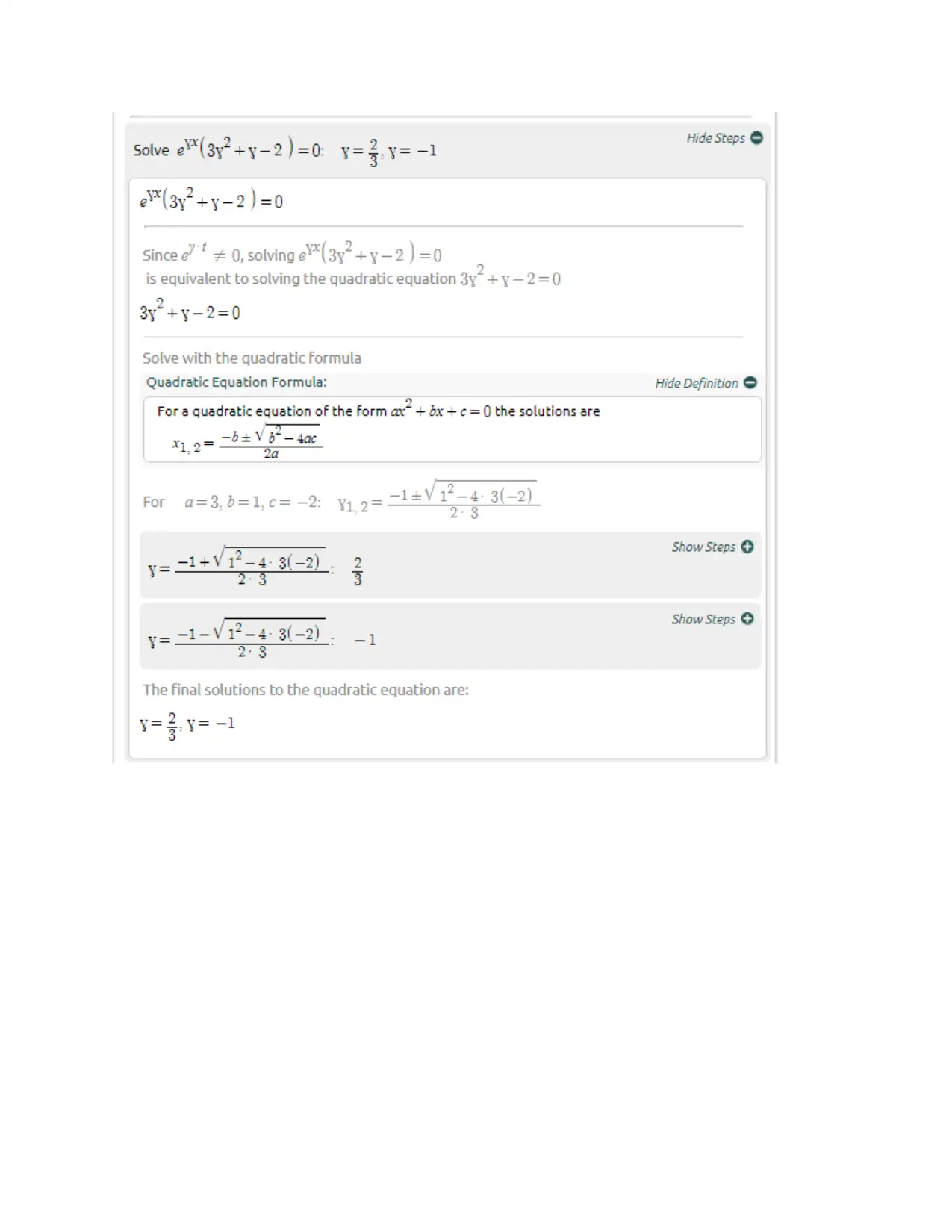
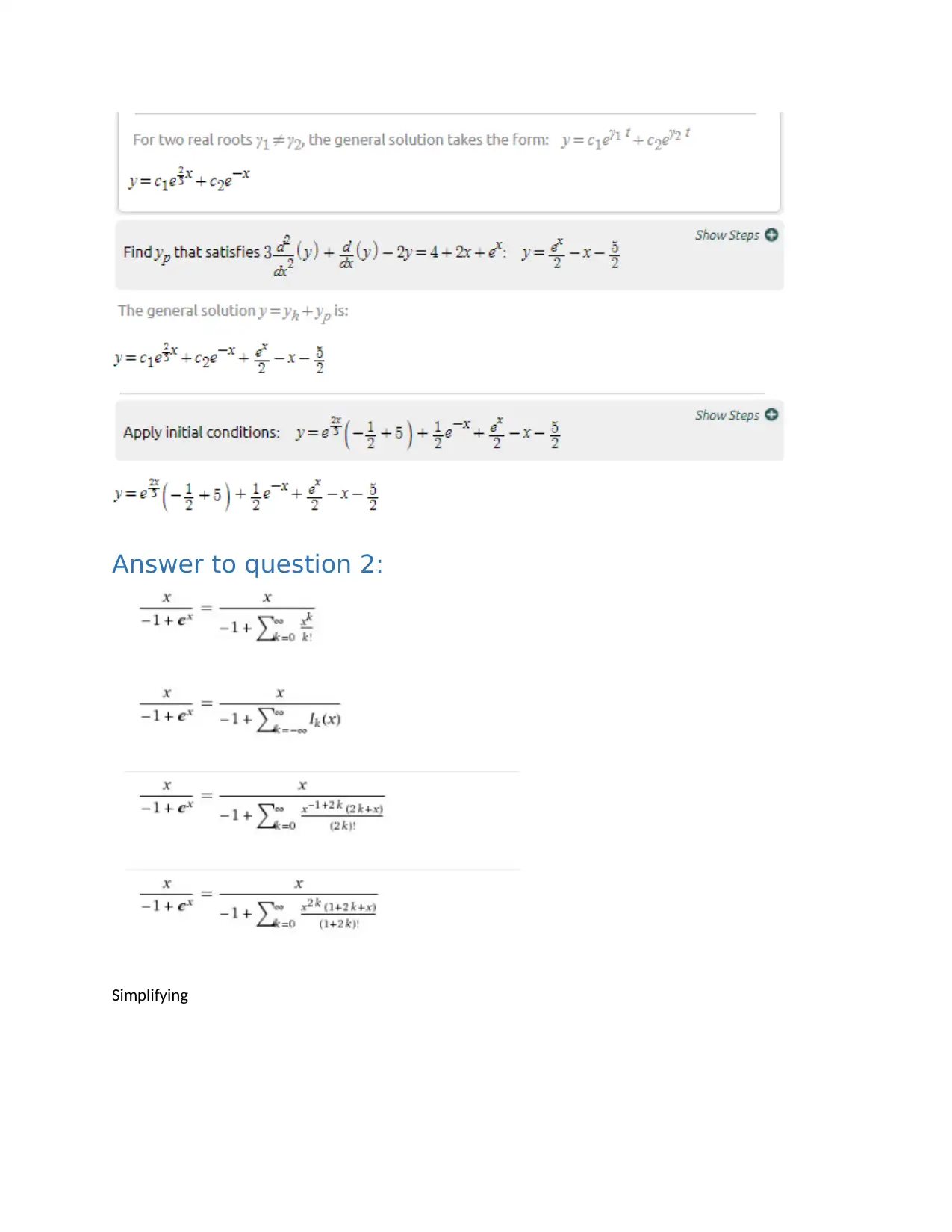
Homework Assignment
AI Summary
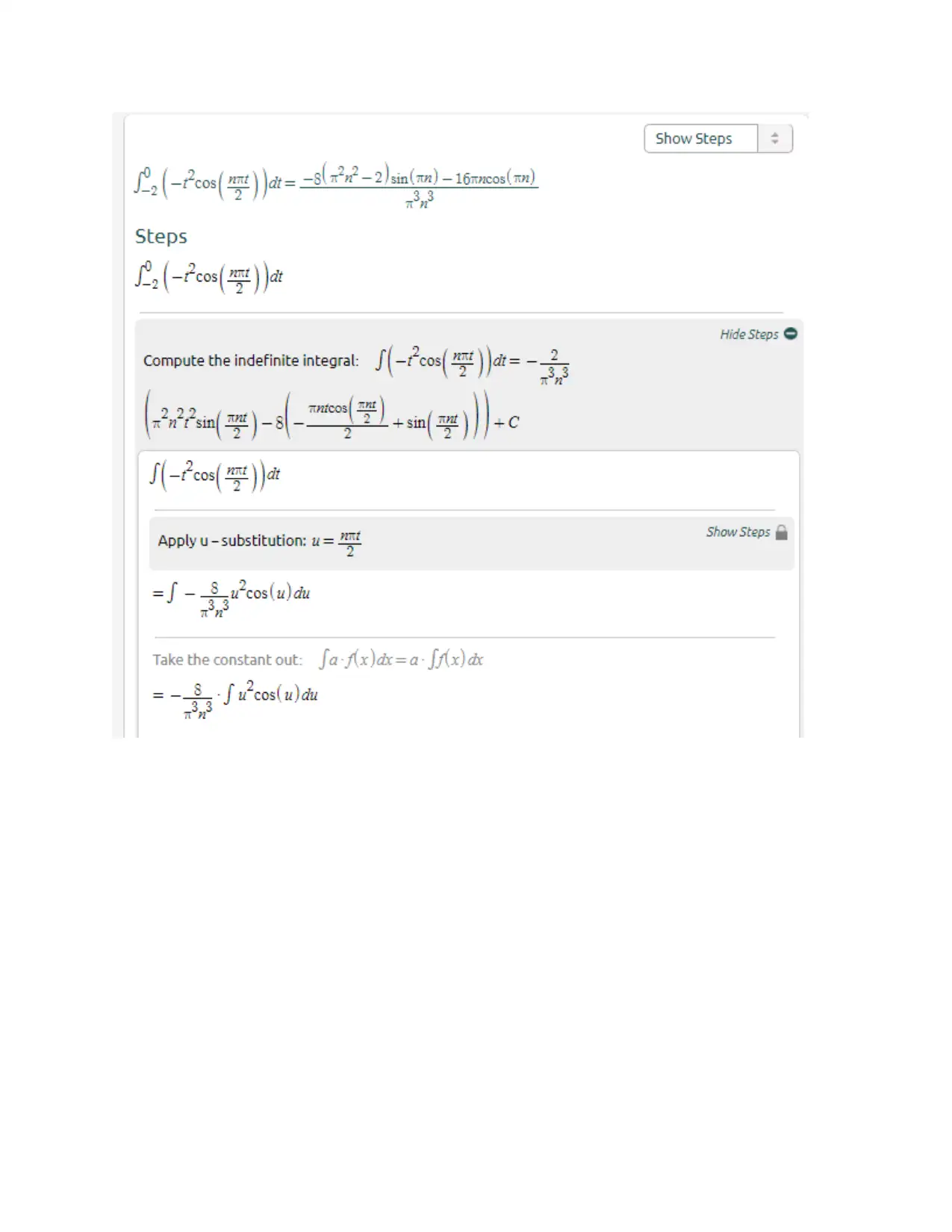
This document presents a comprehensive solution set for Assignment 2 in a Calculus course, likely MAT2100, at a university. The solutions cover a range of calculus topics, beginning with basic problem-solving and progressing to more complex concepts. Specific problems addressed include Fourier series representation, total differential equations, and the evaluation of double integrals, line integrals, and mass calculations. The document provides step-by-step solutions, demonstrating the application of various calculus techniques and theorems. The assignment addresses topics such as even functions, curl of a vector field, and integration over specified regions. The solutions are presented with clear mathematical notation and explanations, making it a valuable resource for students studying calculus.
1 out of 29










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)